gallery
Test matrices
Syntax
Description
[
generates a family of test matrices specified by A1,A2,...,Am] = gallery(matrixname,P1,P2,...,Pn)matrixname.
P1,P2,...,Pn are input parameters required by the individual matrix
family. The number of input parameters P1,P2,...,Pn used in the calling
syntax varies from matrix to matrix. The exact calling syntaxes for each matrix family are
described in the matrixname
section.
[
additionally specifies the data type of the generated test matrices.A1,A2,...,Am] = gallery(matrixname,P1,P2,...,Pn,typename)
Examples
Display Matrix Elements as Scaled Colors
Display matrix elements of several test matrices as scaled colors.
Create a circulant matrix of size 11-by-11. A circulant matrix is a special kind of Toeplitz matrix where each row is obtained from the previous one by cyclically moving the entries one place to the right.
C = gallery('circul',11); Display an image of the matrix elements in C. Add a colorbar to the graph to show the current colormap.
imagesc(C)
axis square
colorbar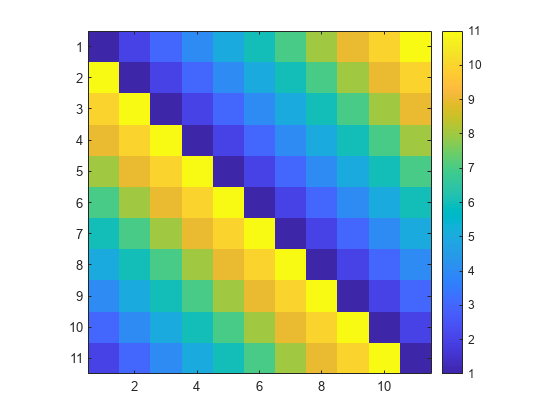
Create a grcar matrix of size 11-by-11. A grcar matrix is a nonsymmetric Toeplitz matrix with -1's on the subdiagonal, 1's on the main diagonal, and 1's on the first few diagonals above the main diagonal.
G = gallery('grcar',11); Display an image of the matrix elements in G.
imagesc(G)
axis square
colorbar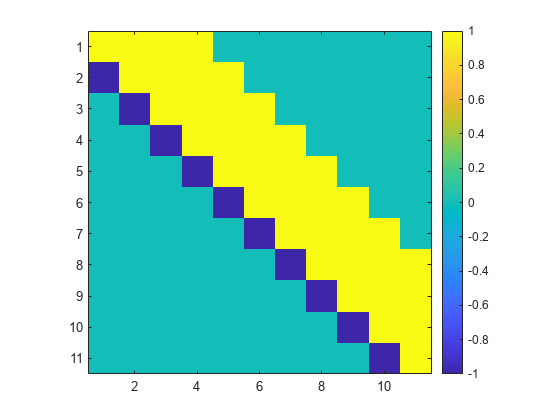
Create a minij matrix of size 11-by-11. A minij matrix M is a symmetric positive definite matrix with elements M(i,j) = min(i,j).
M = gallery('minij',11); Display an image of the matrix elements in M.
imagesc(M)
axis square
colorbar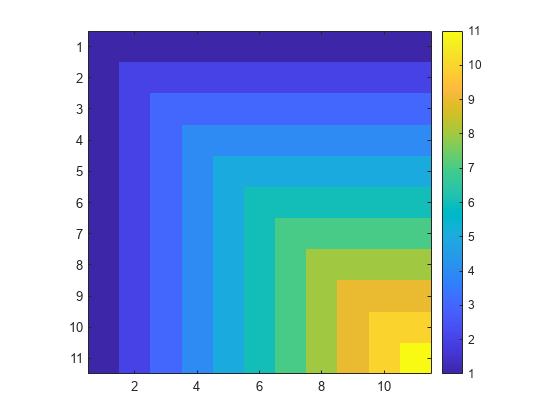
Integer Matrices with Integer Inverses
An integer matrix has an inverse that is also an integer matrix if and only if its determinant is exactly 1 or –1. A square integer matrix with determinant 1 or –1 is also called a unimodular matrix. An example of such a matrix is gallery('dramadah',n), which is an n-by-n matrix of 0's and 1's with determinant 1 or –1.
Create a 6-by-6 dramadah matrix. Calculate its determinant and inverse.
A = gallery('dramadah',6)A = 6×6
1 1 0 1 0 0
0 1 1 0 1 0
0 0 1 1 0 1
1 0 0 1 1 0
1 1 0 0 1 1
0 1 1 0 0 1
detA = det(A)
detA = -1
invA = inv(A)
invA = 6×6
-1 -2 -3 4 -2 5
1 1 1 -2 1 -2
-1 -1 -2 3 -2 4
1 1 2 -2 1 -3
0 1 1 -1 1 -2
0 0 1 -1 1 -1
The inverse of the matrix has only integer entries because the determinant of the original matrix is –1.
Householder Transformation to Compute QR Decomposition
This example shows how to use Householder transformations to compute the QR decomposition of a matrix , where is an orthogonal matrix and is an upper triangular matrix.
First, set the random number generator to the default value, and create a 6-by-3 rectangular matrix of random numbers from the standard normal distribution.
rng('default')
A = randn(6,3)A = 6×3
0.5377 -0.4336 0.7254
1.8339 0.3426 -0.0631
-2.2588 3.5784 0.7147
0.8622 2.7694 -0.2050
0.3188 -1.3499 -0.1241
-1.3077 3.0349 1.4897
To create a Householder matrix, use the function [v,beta] = gallery('house',x). This function takes a column vector , and returns and such that is a Householder matrix. The Householder transformations are used to zero out all but the first element of vector .
Compute a Householder matrix and perform the transformation . The matrix has only zeros below the diagonal in the first column.
[v1,beta1] = gallery('house',A(:,1));
P1 = eye(6) - beta1*(v1*v1');
A1 = P1*AA1 = 6×3
-3.3630 2.8841 1.0421
-0.0000 1.9024 0.0858
0.0000 1.6571 0.5314
-0.0000 3.5028 -0.1350
0.0000 -1.0788 -0.0983
0.0000 1.9227 1.3835
Next, compute a Householder matrix such that has only zeros below the diagonal in the first and second columns.
[v2,beta2] = gallery('house',A1(2:end,2));
v2 = [0;v2];
P2 = eye(6) - beta2*(v2*v2');
A2 = P2*A1A2 = 6×3
-3.3630 2.8841 1.0421
-0.0000 -4.8472 -0.6885
0.0000 0.0000 0.3413
-0.0000 0.0000 -0.5368
0.0000 -0.0000 0.0255
0.0000 0.0000 1.1630
Finally, compute a Householder matrix such that has only zeros in the subdiagonal elements.
[v3,beta3] = gallery('house',A2(3:end,3));
v3 = [0;0;v3];
P3 = eye(6) - beta3*(v3*v3');
R = P3*A2R = 6×3
-3.3630 2.8841 1.0421
-0.0000 -4.8472 -0.6885
-0.0000 0.0000 -1.3258
0.0000 0.0000 0.0000
-0.0000 -0.0000 -0.0000
-0.0000 -0.0000 -0.0000
The matrix is an upper triangular matrix. Since the Householder matrices are involutory (the matrices are equal to their own inverses), the QR decomposition of becomes with .
Q = P1*P2*P3
Q = 6×6
-0.1599 -0.0057 -0.6699 0.4983 -0.2036 -0.4857
-0.5453 -0.3952 -0.1759 -0.6432 0.1342 -0.2895
0.6717 -0.3386 0.1647 -0.0991 0.1551 -0.6109
-0.2564 -0.7239 0.3290 0.5244 0.0805 0.1434
-0.0948 0.2221 -0.0962 0.1872 0.9463 -0.0433
0.3888 -0.3948 -0.6130 -0.1346 0.1203 0.5335
Compare this result with the computation using the qr function.
[Qa,Ra] = qr(A)
Qa = 6×6
-0.1599 -0.0057 -0.6699 0.4983 -0.2036 -0.4857
-0.5453 -0.3952 -0.1759 -0.6432 0.1342 -0.2895
0.6717 -0.3386 0.1647 -0.0991 0.1551 -0.6109
-0.2564 -0.7239 0.3290 0.5244 0.0805 0.1434
-0.0948 0.2221 -0.0962 0.1872 0.9463 -0.0433
0.3888 -0.3948 -0.6130 -0.1346 0.1203 0.5335
Ra = 6×3
-3.3630 2.8841 1.0421
0 -4.8472 -0.6885
0 0 -1.3258
0 0 0
0 0 0
0 0 0
Verify that , within machine precision.
norm(A - Q*R)
ans = 2.2565e-15
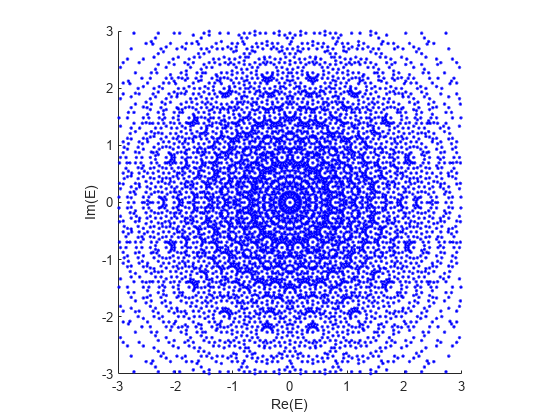
Distribution of Eigenvalues in Complex Plane
This example plots the distribution of eigenvalues from a sample of 20,000 random circulant matrices of size 18-by-18 in the complex plane. The matrix elements are uniformly sampled from the set {–0.4,0.4}.
Create an array E of size 18-by-20,000 to store eigenvalues.
E = zeros(18,20000);
Set the random number generator to the default value. Iterate the following operations 20,000 times in a for-loop statement:
Create a 1-by-18 row vector
xwith random elements of either –0.4 or 0.4.Use the vector
xas an input to create a random circulant matrixA.Find the eigenvalues of
Aand store them inE.
rng('default') for i = 1:20000 x = -0.4 + 0.8*randi([0 1],1,18); A = gallery('circul',x); E(:,i) = eig(A); end
Create a scatter plot to display the eigenvalues E in the complex plane. Set the - and -axis limits to range from –3 to 3.
scatter(real(E(:)),imag(E(:)),'b.') xlabel('Re(E)') ylabel('Im(E)') xlim([-3 3]) ylim([-3 3]) axis square
Perturbation Effect on Eigenvalues of a Matrix
Create the test matrix gallery(3). The test matrix is ill conditioned with eigenvalues that are sensitive to perturbations.
A = gallery(3)
A = 3×3
-149 -50 -154
537 180 546
-27 -9 -25
Compute the eigenvalues of A by using eig.
e = eig(A)
e = 3×1
1.0000
2.0000
3.0000
Compute the eigenvalue condition numbers by using condeig.
c = condeig(A)
c = 3×1
603.6390
395.2366
219.2920
The condition numbers indicate that perturbations in the matrix elements of A can result in perturbations in its eigenvalues with upper bounds that are about 200 to 600 times larger.
Next, make a small perturbation to A by adding a matrix of uniformly distributed random numbers. Set the seed of the random number generator to its default value. Add a random matrix with elements in the interval from 0 to 0.001, exclusive, to A.
rng('default')
Ap = A + 1e-3*rand(3)Ap = 3×3
-148.9992 -49.9991 -153.9997
537.0009 180.0006 546.0005
-26.9999 -8.9999 -24.9990
Compute the eigenvalues of the perturbed matrix Ap.
ep = eig(Ap)
ep = 3×1
0.7399
2.1437
3.1188
Show the difference between the perturbed and the original eigenvalues.
delta = ep - e
delta = 3×1
-0.2601
0.1437
0.1188
Compare the change in the eigenvalues with the upper bounds provided by the eigenvalue condition numbers. The upper bounds have roughly the same order of magnitude as the eigenvalue perturbations.
delta_upper = 1e-3*c
delta_upper = 3×1
0.6036
0.3952
0.2193
Eigenvalues That Are Sensitive to Round-off Errors
Create the test matrix A = gallery(5). The test matrix has eigenvalues that are sensitive to round-off errors.
A = gallery(5)
A = 5×5
-9 11 -21 63 -252
70 -69 141 -421 1684
-575 575 -1149 3451 -13801
3891 -3891 7782 -23345 93365
1024 -1024 2048 -6144 24572
In exact arithmetic, the matrix A has five-fold eigenvalues of (strictly speaking, A has an eigenvalue 0 of algebraic multiplicity 5 and geometric multiplicity 1). This means that the exact characteristic polynomial of A is . Verify that A^5 is a zero matrix.
Afifth = A^5
Afifth = 5×5
0 0 0 0 0
0 0 0 0 0
0 0 0 0 0
0 0 0 0 0
0 0 0 0 0
Compare these results with the numerical computation of eigenvalues using eig. The eig function returns five eigenvalues of A that are small.
e = eig(A)
e = 5×1 complex
-0.0347 + 0.0258i
-0.0347 - 0.0258i
0.0138 + 0.0401i
0.0138 - 0.0401i
0.0419 + 0.0000i
This suggests that the numerical computation of the eigenvalues of A is extremely sensitive to round-off errors due to the floating-point precision used in the computation.
Numerical computations of eigenvalues are very different from their counterparts in exact arithmetic. Instead of finding eigenvalues that are close to the exact eigenvalues of A, the eig function finds eigenvalues of a matrix that is close to A. To illustrate this, plot the exact and numerical eigenvalues of A in the complex plane.
plot(0,0,'bo',real(e),imag(e),'r*') axis([-0.1 0.1 -0.1 0.1]) axis square
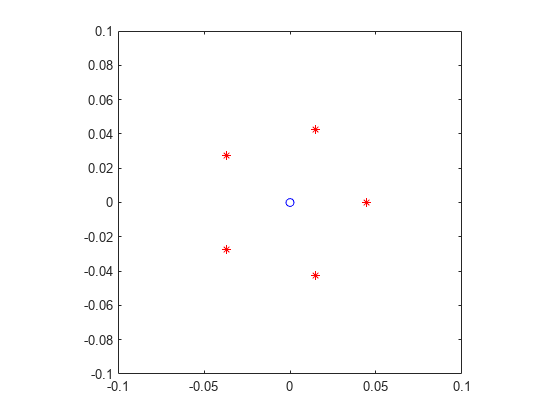
The figure shows that the numerical eigenvalues lie on the vertices of a regular pentagon in the complex plane, centered at the origin. The radius of the pentagon is about 0.04.
Next, compute the eigenvalues of 20 matrices that are close to A. Set the random number generator to the default value, and perturb A by random numbers drawn from the standard normal distribution multiplied by eps. Plot the numerical eigenvalues of the 20 perturbed matrices.
E = zeros(20,5); rng('default') for i = 1:20 E(i,:) = eig(A + eps*randn(5).*A); end plot(0,0,'bo',real(e),imag(e),'r*',real(E),imag(E),'k.') axis([-0.1 0.1 -0.1 0.1]) axis square
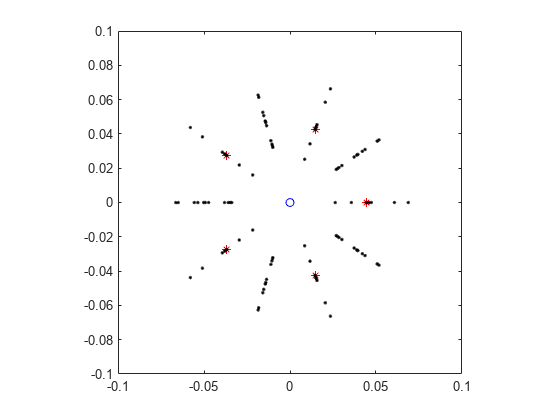
The figure shows that the original pentagon, which represents the eigenvalues of A, can flip orientation when A is perturbed. The eigenvalues of the 20 perturbed matrices lie on the vertices of pentagons with radii in the range of 0.01 to 0.07. The computed eigenvalues of the perturbed matrices behave similarly to the computed eigenvalues of the original matrix. The inaccuracy of the computed eigenvalues is caused by the sensitivity of gallery(5).
Input Arguments
matrixname — Name of matrix family
'binomial' | 'cauchy' | 'chebspec' | 'chebvand' | 'chow' | 'circul' | 'clement' | 'compar' | ...
Name of matrix family, specified as a character vector or string scalar. The
argument matrixname determines the family of generated test matrices
as listed below.
| Description: Binomial matrix, which is a multiple of involutory matrix Syntax:
Properties:
| ||||||||||||||||
| Description: Cauchy matrix Syntax:
Properties:
| ||||||||||||||||
| Description: Chebyshev spectral differentiation matrix Syntax:
Properties:
| ||||||||||||||||
| Description: Vandermonde-like matrix for the Chebyshev polynomials Syntax:
| ||||||||||||||||
| Description: Singular Toeplitz lower Hessenberg matrix Syntax:
Properties:
| ||||||||||||||||
| Description: Circulant matrix Syntax:
Properties:
See also:
| ||||||||||||||||
| Description: Clement tridiagonal matrix with zero diagonal entries Syntax:
Properties:
| ||||||||||||||||
| Description: Comparison matrix Syntax:
Properties:
| ||||||||||||||||
| Description: Counterexamples to matrix condition number estimators Syntax:
| ||||||||||||||||
| Description: Matrix whose columns repeat cyclically Syntax:
| ||||||||||||||||
| Description: Diagonally dominant, ill-conditioned, tridiagonal matrix (sparse matrix) Syntax:
| ||||||||||||||||
| Description: Matrix of zeros and ones Syntax:
| ||||||||||||||||
| Description: Fiedler symmetric matrix Syntax:
Properties:
| ||||||||||||||||
| Description: Forsythe matrix or perturbed Jordan block Syntax:
Properties:
| ||||||||||||||||
| Description: Frank matrix with ill-conditioned eigenvalues Syntax:
Properties:
| ||||||||||||||||
| Description: Greatest common divisor matrix Syntax:
Properties:
| ||||||||||||||||
| Description: Gear matrix Syntax:
Properties:
| ||||||||||||||||
| Description: Toeplitz matrix with sensitive eigenvalues Syntax:
| ||||||||||||||||
| Description: Matrix whose eigenvalues lie on a vertical line in the complex plane Syntax:
| ||||||||||||||||
| Description: Householder matrix Syntax:
| ||||||||||||||||
| Description: Array of randomly sampled integers from uniform distribution on specified range Syntax:
| ||||||||||||||||
| Description: Inverse of an upper Hessenberg matrix Syntax:
Properties:
| ||||||||||||||||
| Description: Involutory matrix (a matrix that is its own inverse) Syntax:
Properties:
See also:
| ||||||||||||||||
| Description: Hankel matrix with factorial elements Syntax:
| ||||||||||||||||
| Description: Jordan block matrix Syntax:
| ||||||||||||||||
| Description: Upper trapezoidal Kahan matrix Syntax:
| ||||||||||||||||
| Description: Kac-Murdock-Szegö Toeplitz matrix Syntax:
Properties:
| ||||||||||||||||
| Description: Krylov matrix Syntax:
| ||||||||||||||||
| Description: Lauchli rectangular matrix Syntax:
Properties:
| ||||||||||||||||
| Description: Lehmer symmetric positive definite matrix Syntax:
Properties:
| ||||||||||||||||
| Description: Matrix of birth numbers and survival rates from the Leslie population model Syntax:
| ||||||||||||||||
| Description: Tridiagonal matrix with real, sensitive eigenvalues Syntax:
Properties:
| ||||||||||||||||
| Description: Lotkin matrix Syntax:
Properties:
| ||||||||||||||||
| Description: Symmetric positive definite matrix Syntax:
Properties:
| ||||||||||||||||
| Description: Moler symmetric positive definite matrix Syntax:
Properties:
| ||||||||||||||||
| Description: Singular matrix from the discrete Neumann problem (sparse matrix) Syntax:
| ||||||||||||||||
| Description: Array of randomly sampled numbers from standard normal (Gaussian) distribution Syntax:
| ||||||||||||||||
| Description: Orthogonal and nearly orthogonal matrices Syntax:
| ||||||||||||||||
| Description: Parter matrix Syntax:
Properties:
| ||||||||||||||||
| Description: Pei matrix Syntax:
| ||||||||||||||||
| Description: Block tridiagonal matrix from Poisson's equation (sparse matrix) Syntax:
| ||||||||||||||||
| Description: Prolate matrix Syntax:
Properties:
| ||||||||||||||||
| Description: Random matrix with normalized columns and specified singular values Syntax:
| ||||||||||||||||
| Description: Random correlation matrix with specified eigenvalues Syntax:
See also:
| ||||||||||||||||
| Description: Random, orthogonal upper Hessenberg matrix Syntax:
| ||||||||||||||||
| Description: Random J-orthogonal matrix Syntax:
| ||||||||||||||||
| Description: Random matrix composed of elements –1, 0 or 1 Syntax:
| ||||||||||||||||
| Description: Random matrix with preassigned singular values Syntax:
| ||||||||||||||||
| Description: Redheffer matrix of ones and zeros Syntax:
Properties:
| ||||||||||||||||
| Description: Matrix associated with the Riemann hypothesis Syntax:
Properties:
| ||||||||||||||||
| Description: Ris matrix Syntax:
| ||||||||||||||||
| Description: Nonsymmetric matrix with ill-conditioned integer eigenvalues Syntax:
Properties:
| ||||||||||||||||
| Description: Complex matrix with a "smoke ring" pseudospectrum Syntax:
Properties:
| ||||||||||||||||
| Description: Symmetric positive definite Toeplitz matrix Syntax:
| ||||||||||||||||
| Description: Pentadiagonal Toeplitz matrix (sparse matrix) Syntax:
| ||||||||||||||||
| Description: Tridiagonal matrix (sparse matrix) Syntax:
| ||||||||||||||||
| Description: Upper triangular matrix discussed by Wilkinson and others Syntax:
Properties:
| ||||||||||||||||
| Description: Array of randomly sampled numbers from standard uniform distribution Syntax:
| ||||||||||||||||
| Description: Wathen matrix (sparse matrix) Syntax:
| ||||||||||||||||
| Description: Various matrices devised or discussed by Wilkinson Syntax:
|
P1,P2,...,Pn — Input parameters
scalars | vectors | matrices
Input parameters, specified as scalars, vectors, or matrices. The parameters
P1,P2,...,Pn used in the calling syntax depend on the matrix family
as discussed in the table in matrixname.
typename — Data type of generated test matrices
character vector | string scalar
Data type of generated test matrices, specified as a character vector or string scalar.
If
typenameis not specified, then the data type of the output matrices is determined from those arguments amongP1,P2,...,Pnthat do not specify matrix dimensions or select an option to determine the character of the output matrices. If any of these arguments is of data typesingle, then the output data type issingle. Otherwise, the output data type isdouble.typenamemust be either'double'or'single'for all test matrices, unlessmatrixnameis'integerdata'. Ifmatrixnameis'integerdata', thentypenamecan be'double','single','int8','int16','int32','uint8','uint16', or'uint32'.
Output Arguments
A1,A2,...,Am — Output coefficients, vectors, matrices, or multidimensional arrays
scalars | vectors | matrices | multidimensional arrays
Output coefficients, vectors, matrices, or multidimensional arrays. The outputs
A1,A2,...,Am that are generated by the calling syntax depend on the
matrix family as discussed in the table in matrixname. In most
cases, the gallery function only returns one matrix as the output
argument.
A — Output matrix or multidimensional array
matrix | multidimensional array
Output matrix or multidimensional array.
References
[1] The MATLAB® gallery of test matrices is based upon the work of Nicholas J. Higham at the Department of Mathematics, University of Manchester, Manchester, England. Further background can be found in the books MATLAB Guide, 2nd ed, by Desmond J. Higham and Nicholas J. Higham, Philadelphia: SIAM, 2005, and Accuracy and Stability of Numerical Algorithms, by Nicholas J. Higham, Philadelphia: SIAM, 1996.
[2] Graham, R.L. and N. J. A. Sloane. “Anti-Hadamard Matrices.“ Linear Algebra and Its Applications 62 (1984): 113-137.
[3] Lippold, G. “Todd, J., Basic Numerical Mathematics. Vol. 2: Numerical Algebra. ISNM 22. Basel-Stuttgart, Birkhäuser-Verlag 1977. 216 S. DM 48,–.“ ZAMM - Zeitschrift für Angewandte Mathematik und Mechanik 59, no. 10 (1979): 589–589.
[4] Gear, C. W. “A Simple Set of Test Matrices for Eigenvalue Programs.“ Mathematics of Computation 23, no. 105 (1969): 119-125.
[5] Lotkin, M. “A Set of Test Matrices.“ Mathematical Tables and Other Aids to Computation 9, no. 52 (1955): 153.
[6] Davies, P. I. and N. J. Higham. “Numerically Stable Generation of Correlation Matrices and Their Factors.” BIT Numerical Mathematics 40 (2000): 640-651.
[7] Barrett, W. W. and T. J. Jarvis. “Spectral Properties of a Matrix of Redheffer.“ Linear Algebra and Its Applications 162-164 (1992): 673-83.
[8] Roesler, F. “Riemann's Hypothesis as an Eigenvalue Problem.“ Linear Algebra and Its Applications 81 (1986): 153-98.
[9] Bondesson, L. and I. Traat. “A Nonsymmetric Matrix with Integer Eigenvalues.“ Linear and Multilinear Algebra 55, no. 3 (2007): 239-47.
[10] Rutishauser, H. “On Test Matrices.“ Programmation en Mathematiques Numeriques, Editions Centre Nat Recherche Sci, Paris, 165 (1966): 349-65.
[11] Wilkinson, J. H. The Algebraic Eigenvalue Problem. Monographs on Numerical Analysis. Oxford: Oxford; New York: Clarendon Press; Oxford University Press, 1988.
[12] Moler, C. B. Numerical Computing with MATLAB. Philadelphia: Society for Industrial and Applied Mathematics, 2004.
Extended Capabilities
Thread-Based Environment
Run code in the background using MATLAB® backgroundPool or accelerate code with Parallel Computing Toolbox™ ThreadPool.
This function fully supports thread-based environments. For more information, see Run MATLAB Functions in Thread-Based Environment.
Version History
Introduced before R2006a
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.

Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list:
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)