impz
Impulse response of digital filter
Syntax
Description
[
returns the impulse response of the digital filter h,t] = impz(d)d. Use designfilt to
generate d based on frequency-response specifications.
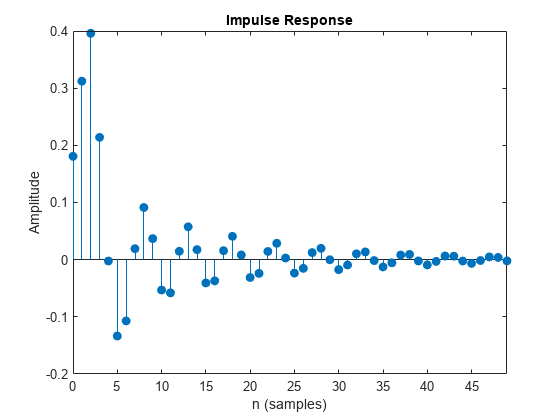
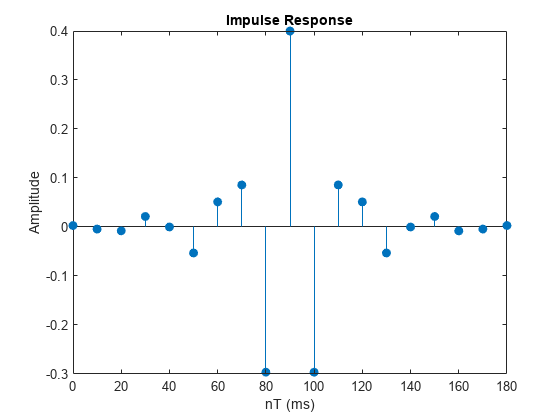
impz(___) with no output arguments plots the impulse
response of the filter.
Examples
Input Arguments
Output Arguments
Algorithms
impz filters a length-n impulse sequence
using
filter(b,a,[1 zeros(1,n-1)])
and plots the result using stem.
Note
If the input to impz is single precision, the function computes the
impulse response using single-precision arithmetic and returns single-precision
output.
When impz calculates n automatically, the
algorithm depends on the properties of the filter:
FIR filters —
nis the length ofb.IIR filters —
impzfirst finds the poles of the transfer function usingroots.If the filter is unstable,
nis chosen to be the point at which the term from the largest pole reaches 106 times its original value.If the filter is stable,
nis chosen as the point at which the term from the largest-amplitude pole is 5 × 10–5 times its original amplitude.If the filter is oscillatory with poles on the unit circle only,
impzcomputes five periods of the slowest oscillation.If the filter has both oscillatory and damped terms,
nis the greater of five periods of the slowest oscillation, or the point at which the term due to the largest pole is 5 × 10–5 times its original amplitude.
impz also allows for delays in the numerator polynomial. The number
of delays is incorporated into the computation of the number of samples.
Extended Capabilities
Version History
Introduced before R2006aSee Also
Apps
Functions
designfilt|digitalFilter|impulse(Control System Toolbox) |impzlength|stem