Duty Cycle of Rectangular Pulse Waveform
This example shows how to create a rectangular pulse waveform and measure its duty cycle. You can think of a rectangular pulse waveform as a sequence of on and off states. One pulse period is the total duration of an on and off state. The pulse width is the duration of the on state. The duty cycle is the ratio of the pulse width to the pulse period. The duty cycle for a rectangular pulse describes the fraction of time that the pulse is on in one pulse period.
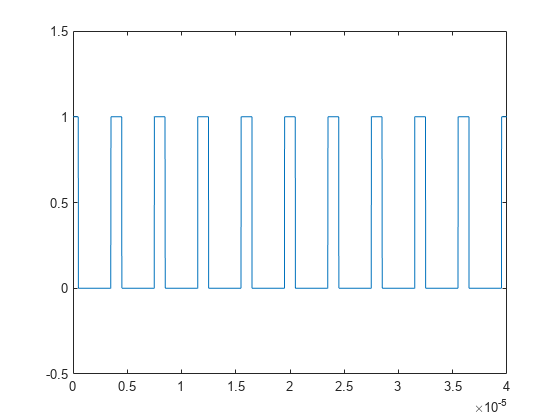
Create a rectangular pulse sampled at 1 gigahertz. The pulse is on, or equal to 1, for a duration of 1 microsecond. The pulse if off, or equal to 0, for a duration of 3 microseconds. The pulse period is 4 microseconds. Plot the waveform.
Fs = 1e9; t = 0:1/Fs:(10*4e-6); pulsewidth = 1e-6; pulseperiods = [0:10]*4e-6; x = pulstran(t,pulseperiods,@rectpuls,pulsewidth); plot(t,x) axis([0 4e-5 -0.5 1.5])
Determine the duty cycle of the waveform using dutycycle. Input both the pulse waveform and the sample rate to output the duty cycle. dutycycle outputs a duty cycle value for each detected pulse.
D = dutycycle(x,Fs)
D = 1×9
0.2500 0.2500 0.2500 0.2500 0.2500 0.2500 0.2500 0.2500 0.2500
In this example, the duty cycle for each of the detected pulses is identical and equal to 0.25. This is the expected duty cycle because the pulse is on for 1 microsecond and off for 3 microseconds in each 4 microsecond period. Therefore, the pulse is on for 1/4 of each period. Expressed as a percentage, this is equal to a duty cycle of 25%.
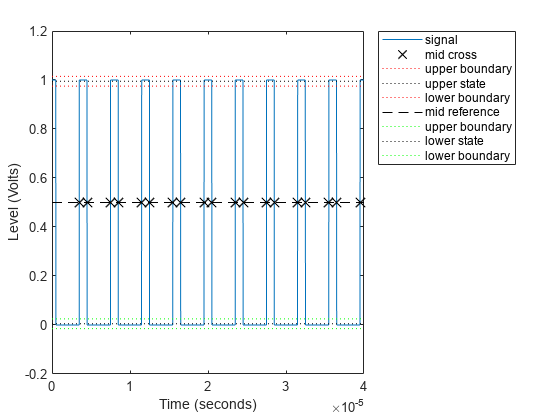
Calling dutycycle with no output arguments produces a plot with all the detected pulse widths marked.
dutycycle(x,Fs);
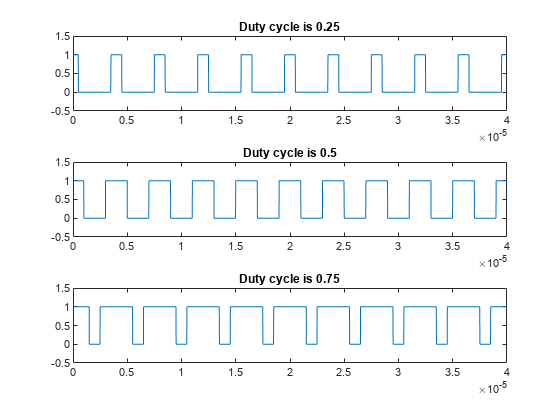
Using the same sample rate and pulse period, vary the pulse on time (pulse width) from 1 to 3 microseconds in a loop and calculate the duty cycle. Plot the pulse waveforms and display the duty cycle value in the plot title for each step through the loop. The duty cycle increases from 0.25 (1/4) to 0.75 (3/4) as the pulse width increases.
nwid = 3; for nn = 1:nwid x = pulstran(t,pulseperiods,@rectpuls,nn*pulsewidth); subplot(nwid,1,nn) plot(t,x) axis([0 4e-5 -0.5 1.5]) D = dutycycle(x,Fs); title(['Duty cycle is ' num2str(mean(D))]) end