Calculus
Using Symbolic Math Toolbox™, you can differentiate and integrate symbolic expressions, perform series expansions, find transforms of symbolic expressions, and perform vector calculus operations by using the listed functions.
When modeling your problem, use assumptions to return the right results. See Use Assumptions on Symbolic Variables. To simplify your results, see Simplify Symbolic Expressions.
Functions
Topics
- Differentiation
Differentiate symbolic expressions and functions.
- Create Symbolic Functions
Use symbolic functions that accept symbolic inputs for analytical calculations.
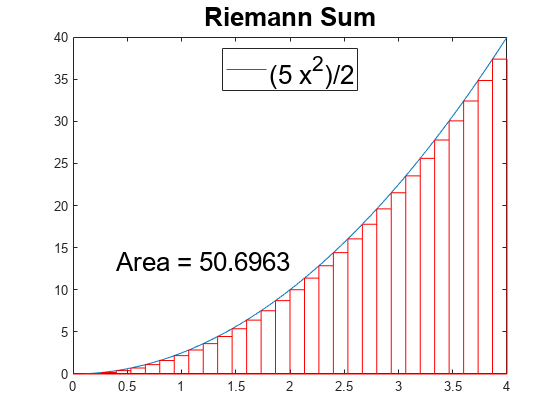
- Integration
Integrate symbolic expressions and functions.
- Taylor Series
Taylor series expansion of symbolic expressions and functions.
- Fourier and Inverse Fourier Transforms
Fourier and inverse Fourier transforms of symbolic expressions.
- Solve Differential Equations of RLC Circuit Using Laplace Transform
Solve differential equations of an RLC circuit by using Laplace and inverse Laplace transforms.
- Solve Difference Equations Using Z-Transform
Z-Transforms and inverses of symbolic expressions and functions.
- Symbolic Summation
Sum symbolic vectors, matrices, or symbolic series.
- Padé Approximant
Pade approximant of symbolic expressions and functions.
- Limits
Limits of symbolic expressions and functions.
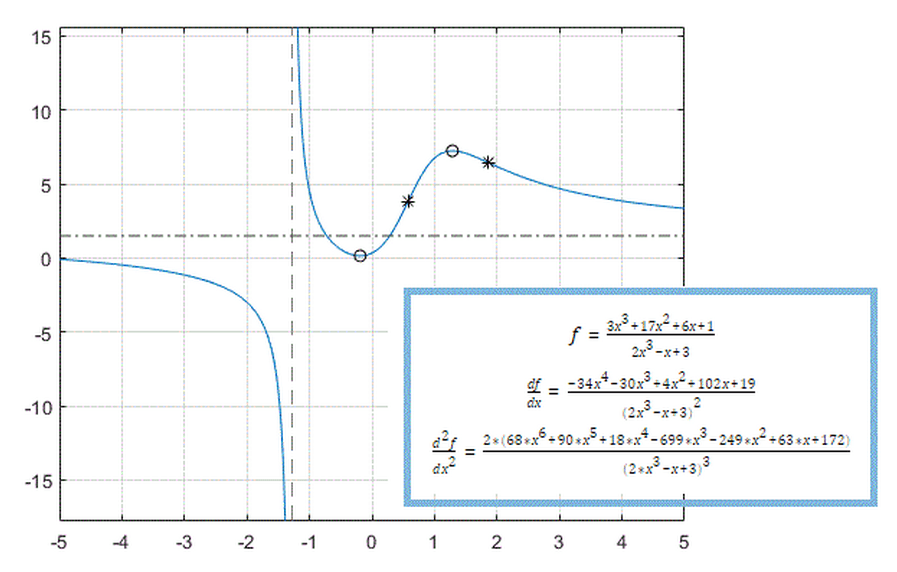
- Find Asymptotes, Critical, and Inflection Points
Find minima, maxima, and asymptotes by using derivatives and limits.
- Functional Derivatives Tutorial
This example shows how to use functional derivatives in Symbolic Math Toolbox using the context of a wave equation.
Related Information
- Teaching Calculus with MATLAB
- Calculus Derivatives (MathWorks Teaching Resources)
- Calculus Integrals (MathWorks Teaching Resources)
- Numerical Methods with Applications (MathWorks Teaching Resources)
- Fourier Analysis (MathWorks Teaching Resources)
- Beam Bending and Deflection (MathWorks Teaching Resources)
- Thermodynamics (MathWorks Teaching Resources)