Heat Conduction in Multidomain Geometry with Nonuniform Heat Flux
This example shows how to perform a 3-D transient heat conduction analysis of a hollow sphere made of three different layers of material.
The sphere is subject to a nonuniform external heat flux.
The physical properties and geometry of this problem are described in Singh, Jain, and Rizwan-uddin (see Reference), which also has an analytical solution for this problem. The inner face of the sphere has a temperature of zero at all times. The outer hemisphere with positive value has a nonuniform heat flux defined by
and are azimuthal and elevation angles of points in the sphere. Initially, the temperature at all points in the sphere is zero.
Create a multilayered sphere using the multisphere function. The sphere has three layers of material with a hollow inner core.
gm = multisphere([1,2,4,6],"Void",[true,false,false,false]);Plot the geometry with cell and face labels. Use a FaceAlpha of 0.25 so that labels of the interior layers are visible.
pdegplot(gm,FaceAlpha=0.25,CellLabel="on")
pdegplot(gm,FaceAlpha=0.25,FaceLabel="on")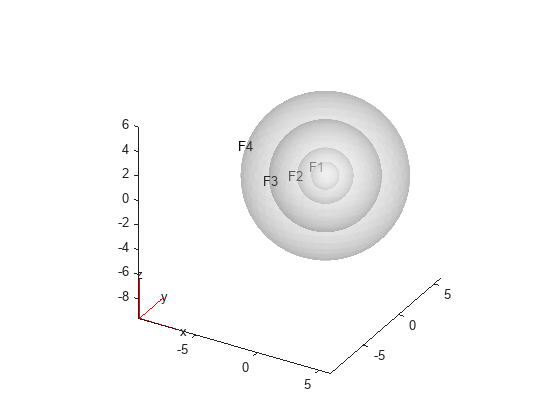
Create an femodel object for transient thermal analysis and include the geometry.
model = femodel(AnalysisType="thermalTransient", ... Geometry=gm);
Generate a mesh for the geometry. Choose a mesh size that is coarse enough to speed the solution, but fine enough to represent the geometry reasonably accurately.
model = generateMesh(model,Hmax=1);
Specify the thermal conductivity, mass density, and specific heat for each layer of the sphere. The material properties are dimensionless values, not given by realistic material properties.
model.MaterialProperties(1) = ... materialProperties(ThermalConductivity=1, ... MassDensity=1, ... SpecificHeat=1); model.MaterialProperties(2) = ... materialProperties(ThermalConductivity=2, ... MassDensity=1, ... SpecificHeat=0.5); model.MaterialProperties(3) = ... materialProperties(ThermalConductivity=4, ... MassDensity=1, ... SpecificHeat=4/9);
Specify boundary conditions. The innermost face has a temperature of zero at all times.
model.FaceBC(1) = faceBC(Temperature=0);
The outer surface of the sphere has an external heat flux. Use the functional form of thermal boundary conditions to define the heat flux.
function Qflux = externalHeatFlux(region,~) [phi,theta,~] = cart2sph(region.x,region.y,region.z); theta = pi/2 - theta; % transform to 0 <= theta <= pi ids = phi > 0; Qflux = zeros(size(region.x)); Qflux(ids) = ... theta(ids).^2.*(pi - ... theta(ids)).^2.*phi(ids).^2.*(pi - phi(ids)).^2; end
Plot the flux on the surface.
[phi,theta,r] = meshgrid(linspace(0,2*pi),linspace(-pi/2,pi/2),6); [x,y,z] = sph2cart(phi,theta,r); region.x = x; region.y = y; region.z = z; flux = externalHeatFlux(region,[]); figure surf(x,y,z,flux,LineStyle="none") axis equal view(130,10) colorbar xlabel("x") ylabel("y") zlabel("z") title("External Flux")

Include this boundary condition in the model.
model.FaceLoad(4) = faceLoad(Heat=@externalHeatFlux);
Define the initial temperature to be zero at all points.
model.CellIC = cellIC(Temperature=0);
Define a time-step vector and solve the transient thermal problem.
tlist = [0,2,5:5:50]; R = solve(model,tlist);
To plot contours at several times, with the contour levels being the same for all plots, determine the range of temperatures in the solution. The minimum temperature is zero because it is the boundary condition on the inner face of the sphere.
Tmin = 0;
Find the maximum temperature from the final time-step solution.
Tmax = max(R.Temperature(:,end));
Plot contours in the range Tmin to Tmax at the times in tlist.
h = figure; for i = 1:numel(tlist) pdeplot3D(R.Mesh,ColorMapData=R.Temperature(:,i)) clim([Tmin,Tmax]) view(130,10) title(["Temperature at Time " num2str(tlist(i))]); M(i) = getframe; end


To see a movie of the contours when running this example on your computer, execute the following line:
movie(M,2)
Visualize the temperature contours on the cross-section. First, define a rectangular grid of points on the plane where .
[YG,ZG] = meshgrid(linspace(-6,6,100),linspace(-6,6,100)); XG = zeros(size(YG));
Interpolate the temperature at the grid points. Perform interpolation for several time steps to observe the evolution of the temperature contours.
tIndex = [2,3,5,7,9,11];
varNames = {'Time_index','Time_step'};
index_step = table(tIndex.',tlist(tIndex).',VariableNames=varNames);
disp(index_step); Time_index Time_step
__________ _________
2 2
3 5
5 15
7 25
9 35
11 45
TG = interpolateTemperature(R,XG,YG,ZG,tIndex);
Define the geometric spherical layers on the cross-section.
t = linspace(0,2*pi); ylayer1 = cos(t); zlayer1 = sin(t); ylayer2 = 2*cos(t); zlayer2 = 2*sin(t); ylayer3 = 4*cos(t); zlayer3 = 4*sin(t); ylayer4 = 6*cos(t); zlayer4 = 6*sin(t);
Plot the contours in the range Tmin to Tmax for the time steps corresponding to the time indices tIndex.
figure("Position",[10,10,1000,550]); for i = 1:numel(tIndex) subplot(2,3,i) contour(YG,ZG,reshape(TG(:,i),size(YG)),ShowText="on") colorbar title(["Temperature at Time " num2str(tlist(tIndex(i)))]); hold on clim([Tmin,Tmax]) axis equal % Plot boundaries of spherical layers for reference. plot(ylayer1,zlayer1,"k",LineWidth=1.5) plot(ylayer2,zlayer2,"k",LineWidth=1.5) plot(ylayer3,zlayer3,"k",LineWidth=1.5) plot(ylayer4,zlayer4,"k",LineWidth=1.5) end

Reference
[1] Singh, Suneet, P. K. Jain, and Rizwan-uddin. "Analytical Solution for Three-Dimensional, Unsteady Heat Conduction in a Multilayer Sphere." ASME. J. Heat Transfer. 138(10), 2016, pp. 101301-101301-11.
