patternElevation
System object: phased.HeterogeneousConformalArray
Namespace: phased
Plot heterogeneous conformal array directivity or pattern versus elevation
Syntax
patternElevation(sArray,FREQ)
patternElevation(sArray,FREQ,AZ)
patternElevation(sArray,FREQ,AZ,Name,Value)
PAT = patternElevation(___)
Description
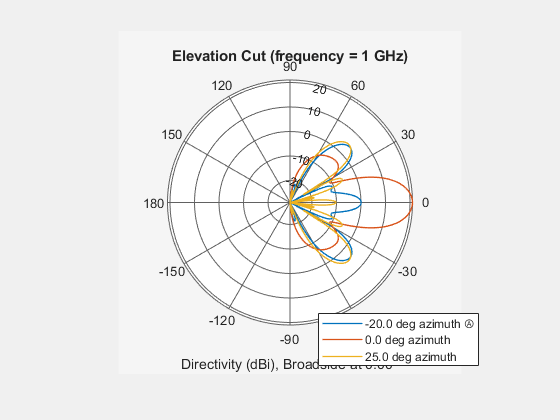
patternElevation( plots
the 2-D array directivity pattern versus elevation (in dBi) for the
array sArray,FREQ)sArray at zero degrees azimuth angle. When AZ is
a vector, multiple overlaid plots are created. The argument FREQ specifies
the operating frequency.
The integration used when computing array directivity has a minimum sampling grid of 0.1 degrees. If an array pattern has a beamwidth smaller than this, the directivity value will be inaccurate.
patternElevation(,
in addition, plots the 2-D element directivity pattern versus elevation
(in dBi) at the azimuth angle specified by sArray,FREQ,AZ)AZ.
When AZ is a vector, multiple overlaid plots
are created.
patternElevation(
plots the array pattern with additional options specified by one or
more sArray,FREQ,AZ,Name,Value)Name,Value pair arguments.
PAT = patternElevation(___)PAT is a matrix whose entries
represent the pattern at corresponding sampling points specified by
the 'Elevation' parameter and the AZ input
argument.
Input Arguments
Name-Value Arguments
Output Arguments
Examples
More About
Version History
Introduced in R2015a