Fit Proton Bragg Peaks
Proton Bragg Peak Fit
Feature
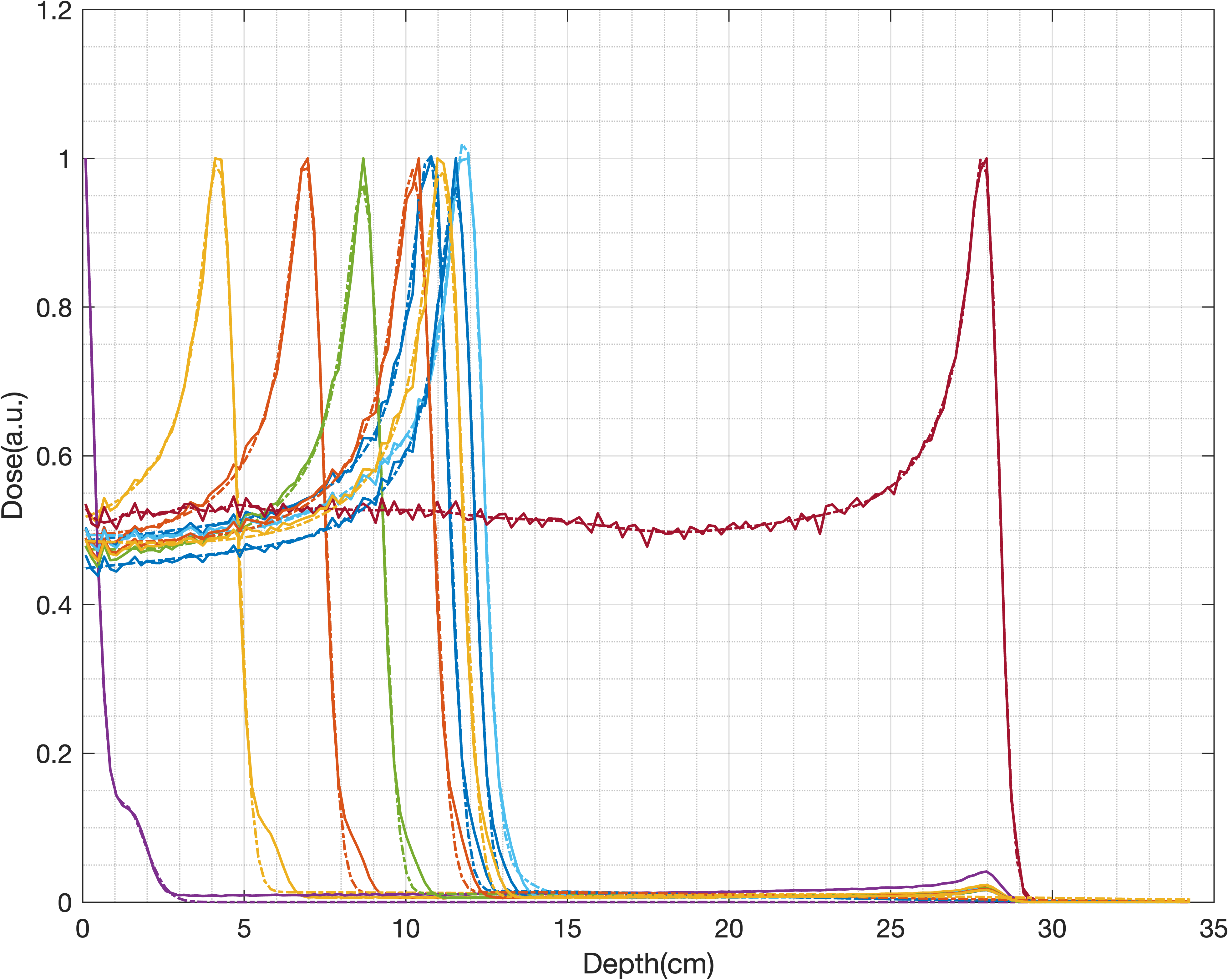
- Fit IDD curve with Bortfeld functions, IDD curve may contains multiple bragg peaks.
- Reconstruct 2D/3D proton dose from measurement of MLSIC[5], (multi-gauss model in XY plane, bortfeld in Z)
- Proton Radiography/CT with feature 1 and 2
- Provide IDD measurement data and simulation data, data acquired from Zebra and MLSIC which can be used in Proton Radiographics
- Bortfeld function implemented in C++, provide IDD, mean gradient and jacobian outputs.
- Input Integral Depth Dose(IDD) is suggested to rescale to [0,10] or nomalize to [0,1], but it's ok to fit raw data in any scale
- Compiled with Visual Studio + Intel OneAPI, faster than mex in MATLAB. Highly recommanded to compile the src with VS and Intel OneAPI
- Support Apple Silicon (Matlab R2022a, Matlab R2022a beta don't have toolboxs)
- Image Processing Toolbox, Optimization Toolbox and Signal Processing Toolbox required
bragg-peak fitting are ready to use.
Dose reconstruction Working in progress
How to use:
examples: ./utils/demo.m
Windows
- Pre-compiled functions are provided.
-
BortfeldFunction.mexw64Windows with avx2(supported by most of modern x86_64 CPU).
-
- If Pre-compiled functions not work, run
./src/compile_PBPF.mto compile it
MacOS
- Pre-compiled functions are provided.
-
BortfeldFunction.mexmaca64for Apple Silicon Mac (do not Support AVX) -
BortfeldFunction.mexmacai64for Intel Mac (AVX not used)
-
- If Pre-compiled functions not work, run
./src/compile_PBPF.mto compile it
Linux
- Pre-compiled functions are Not provided.
-
BortfeldFunction_avx512f.mexa64Linux with avx512f (Only some x86_64 CPU support this) If you use this, change BortfeldFunction in bf_mex to BortfeldFunction_avx512f -
BortfeldFunction.mexa64Linux with avx2(supported by most of modern x86_64 CPU)
-
- If Pre-compiled functions not work, run
./src/compile_PBPF.mto compile it
Compilation
- All precompiled mex function can work with both
singleanddouble, butsinglenumbers can not be used for finite difference optimization(double precision required). Use the gradient provided by mex function. - Open the root folder run
cd('./src')in matlab - run
compile_PBPFthree compile flags are provided- use_openmp = 1; Use OpenMP
- use_avx = 1; Use AVX2
- is_avx512 = 1; Use AVX512 (not every CPU support this)
Here are some code snippets
- predict IDD with depth and bf parameters
z = (1:64)*0.3; % depth unit(cm), (n,1) size is preferred
% bortfeld function parameters, [range1,sigma1,epsilon1,phi1, range2,sigma2,epsilon2,phi2] two bragg-peaks used here, range unit is cm
bf_para = [15,0.3,1e-3,0.4, 12,0.4,1e-3,0.4];
% get idd curve, size of output will be (n,1), no matter z is (1,n) or (n,1)
output = bf_mex(z,bf_para,'idd');
plot(z,output);
grid on;
grid minor;
xlabel('Depth(cm)');
ylabel('Dose(a.u.)');% a.u. means arbitary unit
% for short
% output = bf_mex((1:64)*0.3,[15,0.3,1e-3,0.4, 12,0.4,1e-3,0.4],'idd')- Fit measured IDD
% method 1
[x,idd_o] = precise_fit(z,idd_i,num_bp,strict);
% method 2 used for fast fit, don't calculate IDD in this function
x = fast_fit(z,idd_i,num_bp);
idd_o = bf_mex(z,x,'idd');- Get gradient (Jacobian matrix) of Bortfeld function
z = (1:64)*0.3; % depth unit(cm), (n,1) size is preferred
% bortfeld function parameters, (m,1), range unit is cm
bf_para = [15,0.3,1e-3,0.4, 12,0.4,1e-3,0.4];
% output size will be (n,m)
output = bf_mex((1:64)'*0.3,[15,0.3,1e-3,0.4, 12,0.4,1e-3,0.4],'jacobian')- Other functions
- stored in
./utils/ - If matlab crashed on Rosseta Matlab, run this function
ifMacCrashed()
- stored in
- Benchmark of mex functions
./utils/test_mex_func.m, further optimization required.
% BortfeldFunction time: single(0.249554s), double(0.248533s)
% BortfeldFunction Grad time: single(2.758517s), double(2.772066s)
% Gauss2D Grad GPU time: single(0.942952s), double(1.575574s)
% Gauss2D Grad CPU time: single(0.131198s), double(0.201214s)
% Gauss2D GPU time: single(0.196284s), double(0.450232s)
% Gauss2D CPU time: single(0.842755s), double(0.665228s)
% ProtonDose3D GPU time: single(0.493263s), double(0.537123s)
% ProtonDose3D CPU time: single(0.751850s), double(0.496489s)s5cuGAUFbX1a
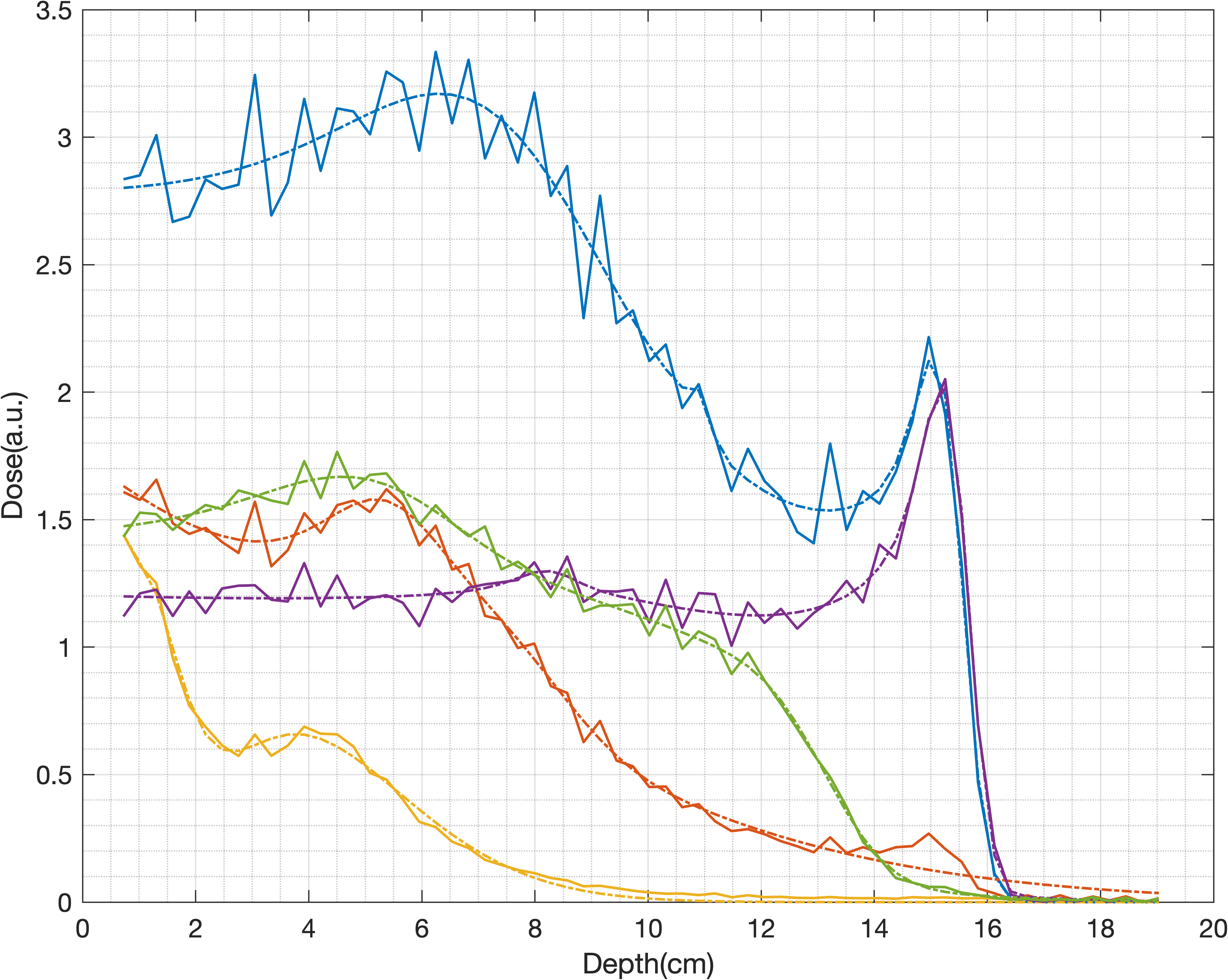
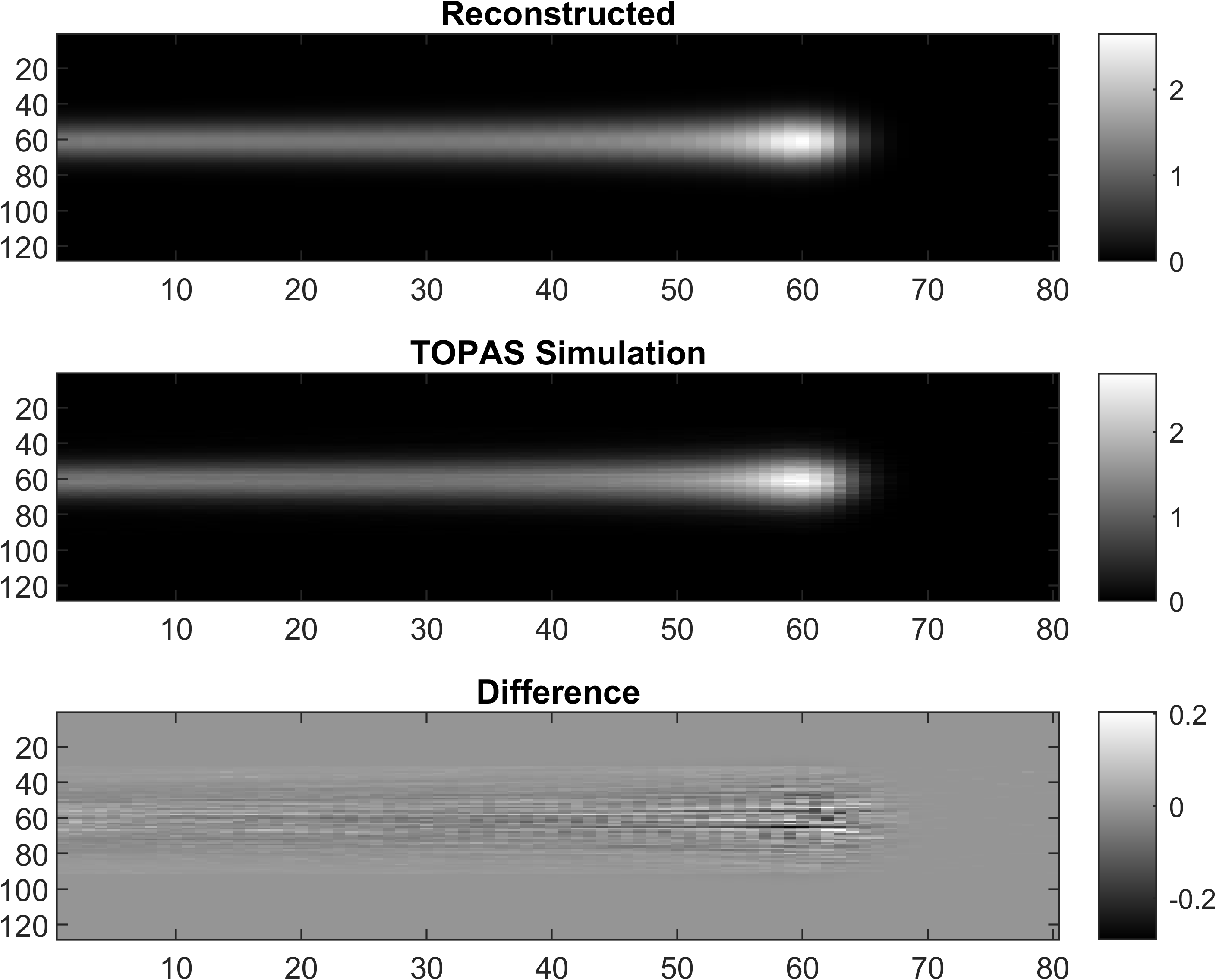
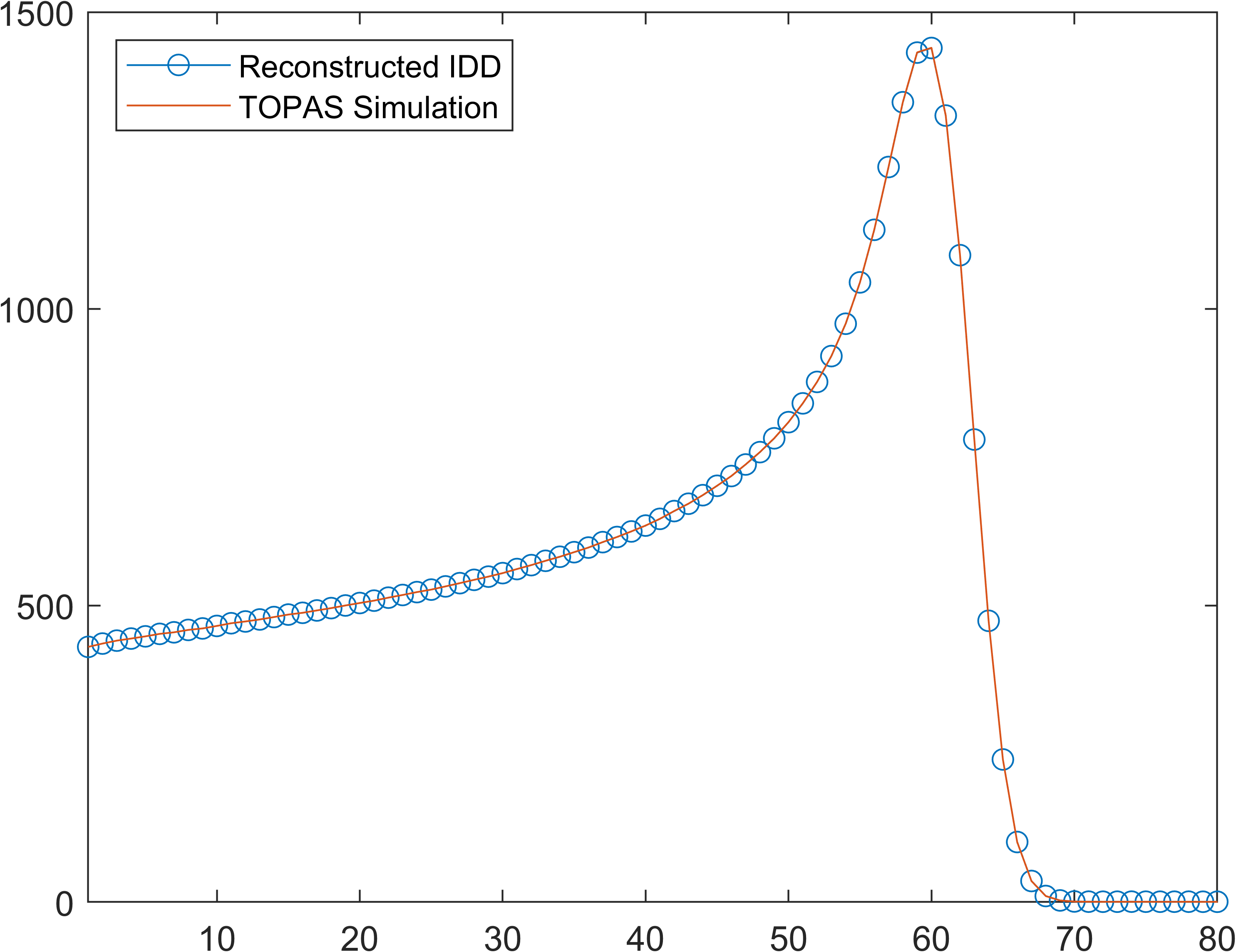
1D IDD data
Applications can be found in ./utils/demo.m and data stored in ./data/. Be careful, run the demo section by section, some parts are time comsuming.
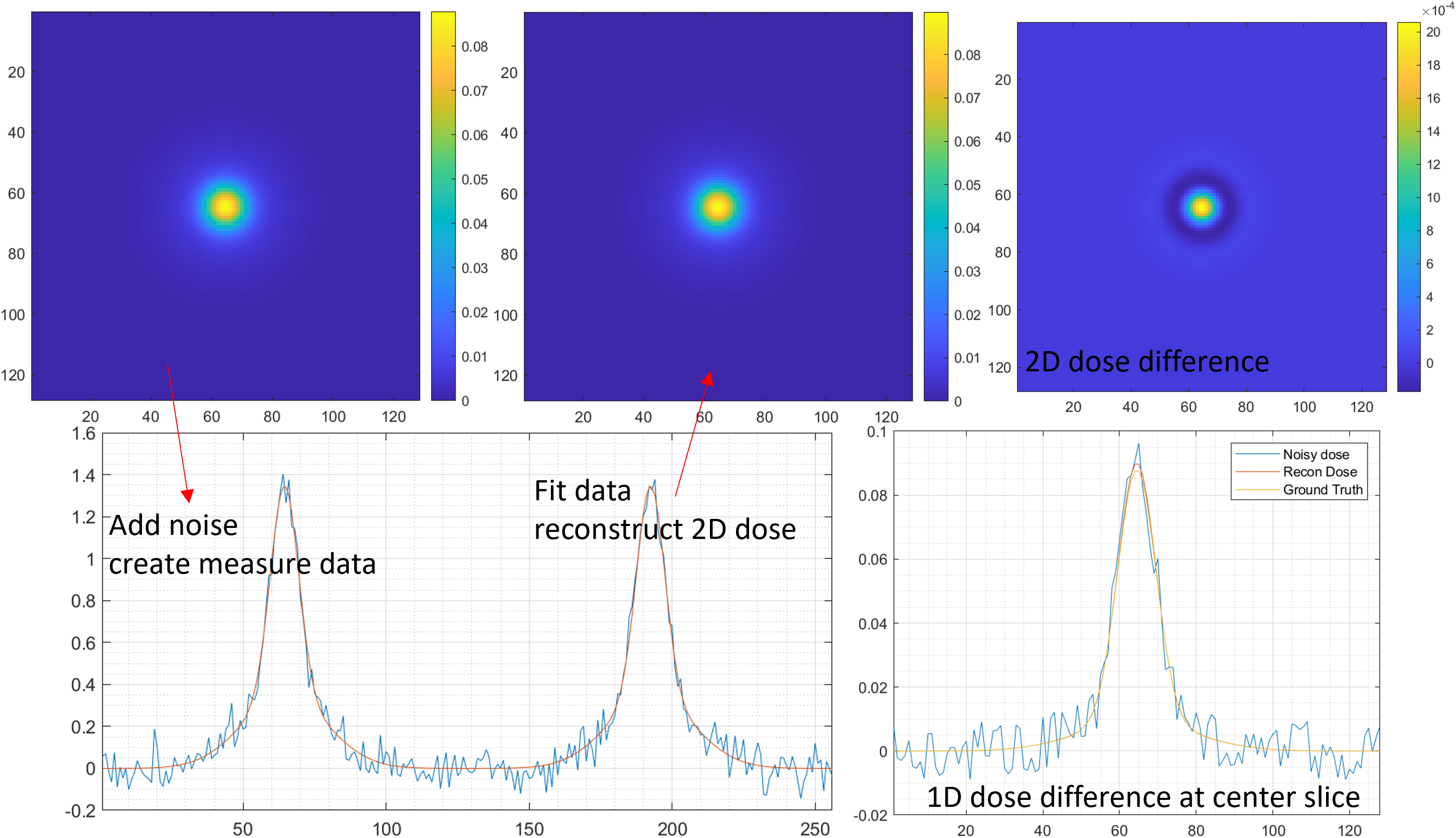
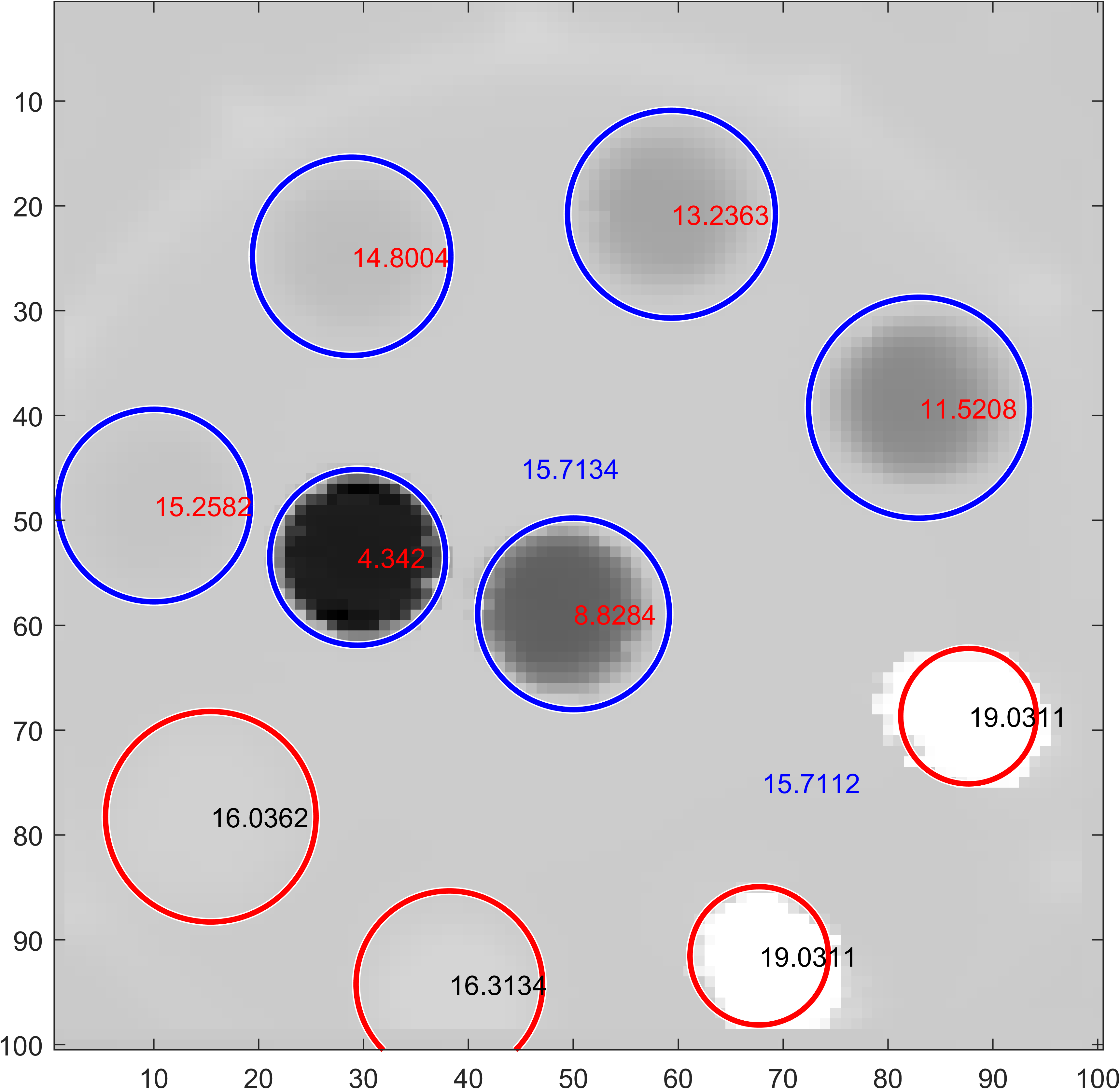
2D dose reconstruction
Strip ionization chamber array[4,5] were used for QA purpose, two layers of horizontal and vertical strip detectors were used to locate the proton beam position.Details
| White Noise level(divide by max dose) | Max Absolute Error( <math-renderer class="js-inline-math" style="display: inline" data-static-url="https://github.githubassets.com/static" data-run-id="48b536abf7cf51b9a6cde2f0de740e48">$\frac{\max|error|}{max[dose]}$</math-renderer>) |
|---|---|
| 30% | 0.0441 |
| 20% | 0.0337 |
| 10% | 0.0192 |
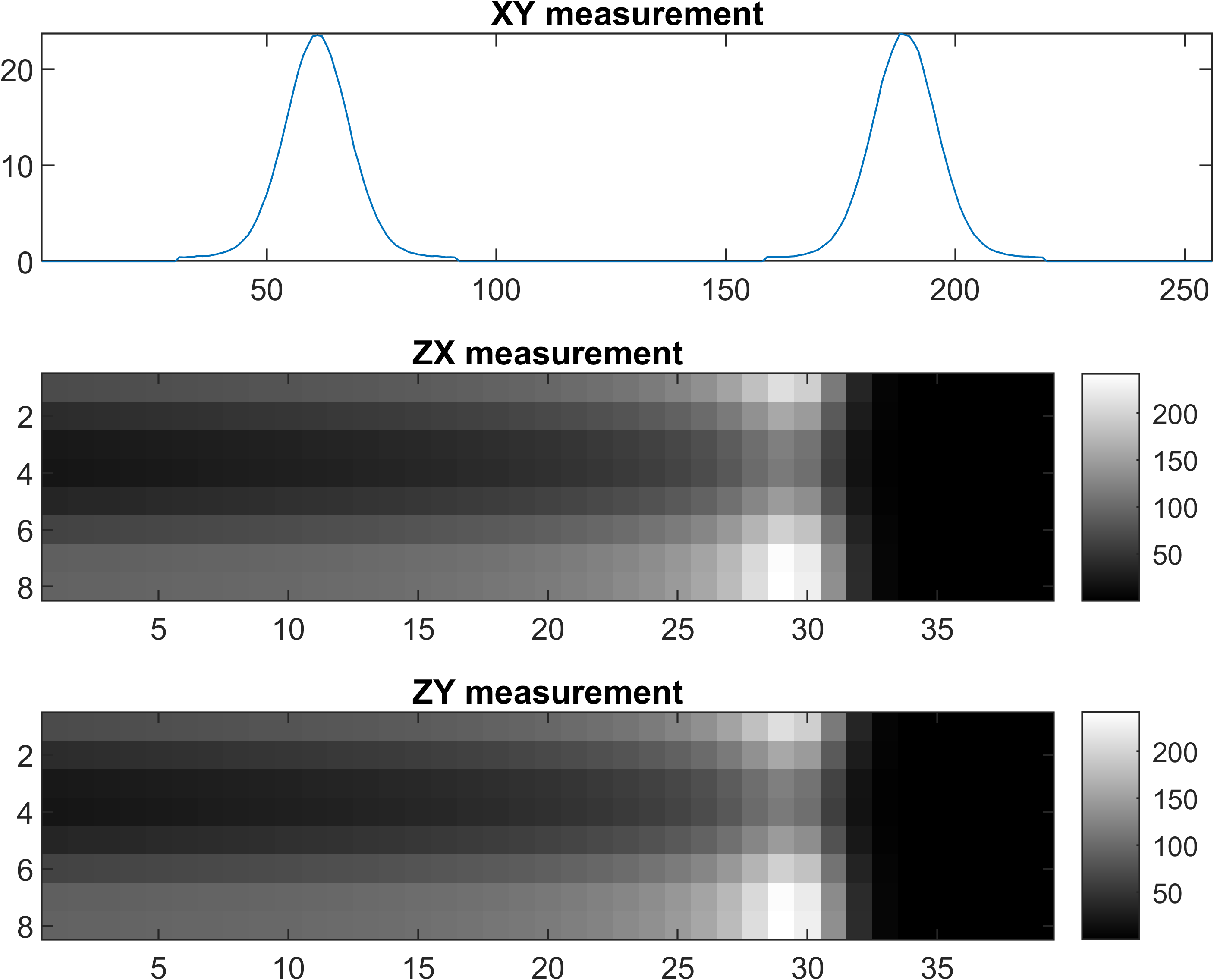
3D dose reconstruction
Only MLSIC can measure a 3D dose in real time[5], it contains 768 ADC channels (XY: 128x2, ZX: 8x32, ZY: 8x32) Details. The measurement function of MLSIC can be defined as a function, <math-renderer class="js-inline-math" style="display: inline" data-static-url="https://github.githubassets.com/static" data-run-id="48b536abf7cf51b9a6cde2f0de740e48">$f: \R^{128\times128\times66} \rightarrow \R^{128\times2 + 8\times32 + 8\times32}$</math-renderer>
Symmetric dose
Asymetric dose
to be updated
Proton Radiography
| Head Phantom | Simulation | MLSIC data |
|---|---|---|
 |
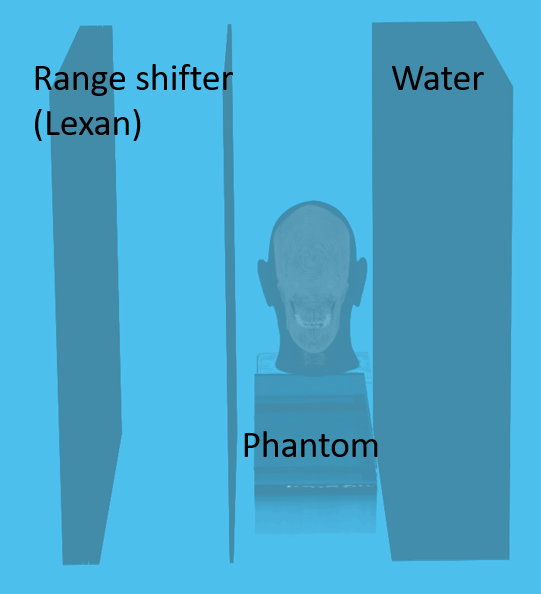 |
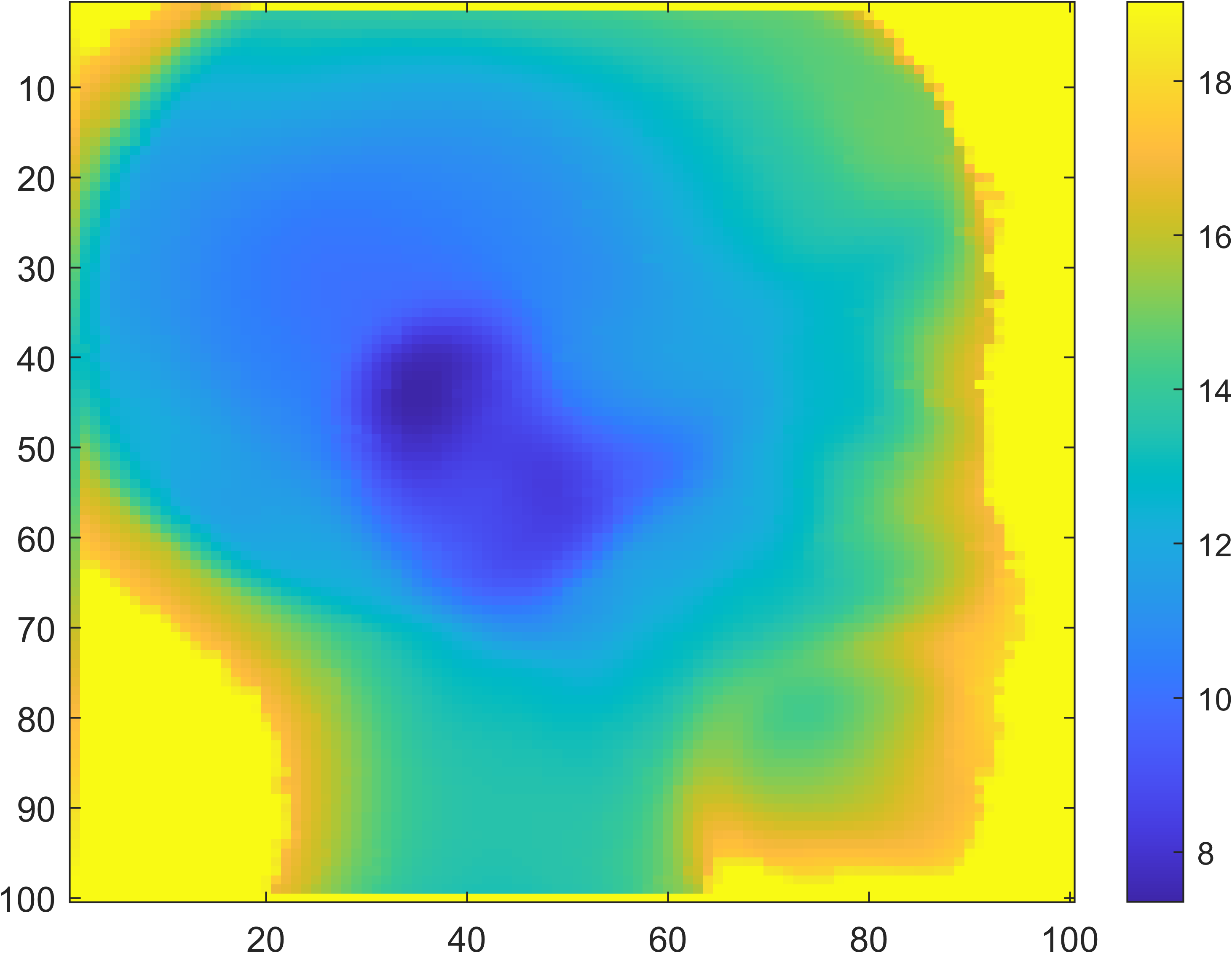 |
Proton CT
to be updated
Details of math and MLSIC structures can be found in here
Reference :
- An analytical approximation of the Bragg curve for therapeutic proton beams
- E. Cojocaru. Parabolic Cylinder Functions
- On the parametrization of lateral dose profiles in proton radiation therapy
- A 2D strip ionization chamber array with high spatiotemporal resolution for proton pencil beam scanning FLASH radiotherapy
- A multi-layer strip ionization chamber (MLSIC) device for proton pencil beam scan quality assurance
- Evaluation of the influence of double and triple Gaussian proton kernel models on accuracy of dose calculations for spot scanning technique
Remark:
M1 mac openmp issue: https://www.mathworks.com/matlabcentral/answers/1761950-m1-mac-compile-mex-file-with-openmp?s_tid=srchtitle
Matlab R2022a thread safty is not very stable, if the mex function crashed matlab, run the magic function 'test3_mex.mexmaci64' by calling test3_mex(int32(16));. Its output looks like
i = 1
i = 2
i = 7
i = 8
i = 5
i = 6
i = 3
i = 4
i = 9
i = 10
i = 13
i = 11
i = 14
i = 15
i = 12
i = 16
Matlab R2022a beta works well with openmp but it do not support official toolbox.
Cite As
shuang zhou (2025). Fit Proton Bragg Peaks (https://github.com/civerjia/Proton-Bragg-Peak-Fit/releases/tag/v1.3.0), GitHub. Retrieved .
MATLAB Release Compatibility
Platform Compatibility
Windows macOS LinuxTags
Community Treasure Hunt
Find the treasures in MATLAB Central and discover how the community can help you!
Start Hunting!Discover Live Editor
Create scripts with code, output, and formatted text in a single executable document.
src
utils
| Version | Published | Release Notes | |
|---|---|---|---|
| 1.3.0 | See release notes for this release on GitHub: https://github.com/civerjia/Proton-Bragg-Peak-Fit/releases/tag/v1.3.0 |
||
| 1.2.1 | See release notes for this release on GitHub: https://github.com/civerjia/Proton-Bragg-Peak-Fit/releases/tag/v1.2.1 |
||
| 1.2.0 | See release notes for this release on GitHub: https://github.com/civerjia/Proton-Bragg-Peak-Fit/releases/tag/v1.2.0 |
||
| 1.1.0 | See release notes for this release on GitHub: https://github.com/civerjia/Proton-Bragg-Peak-Fit/releases/tag/v1.1.0 |
||
| 1.0.1 | add cpp files |
||
| 1.0.0 |