Sensor Fusion for Orientation Estimation
From the series: Perception
Sensors are a key component of an autonomous system, helping it understand and interact with its surroundings. In this video, Roberto Valenti joins Connell D'Souza to demonstrate using Sensor Fusion and Tracking Toolbox™ to perform sensor fusion of inertial sensor data for orientation estimation. This is a common and important application for teams participating in maritime and aerial vehicle competitions.
First, Connell and Roberto introduce common inertial sensors like inertial measurement units (IMU) and magnetic, angular rate, and gravity (MARG) before explaining why sensor fusion is important to make sense of this sensor data.
Roberto will then use MATLAB Mobile™ to stream and log accelerometer, gyroscope, and magnetometer sensor data from his cell phone to MATLAB® and perform sensor fusion on this data to estimate orientation using only a few lines of code. The imufilter and ahrsfilter functions used in this video use Kalman filter-based fusion algorithms. The results of the fusion are compared with the orientation values streamed from the cell phone to check the accuracy of the estimation.
Download the files used in this video from MATLAB Central File Exchange
Additional Links:
Published: 8 Nov 2018
Hello, everyone. Welcome to another episode of the Matlab and Simulink Robotics Arena. On today's episode, we're going to talk about sensor fusion for orientation estimation. And to join me to talk about this interesting topic I've got my close friend and colleague Roberto Valenti. Roberto, why don't you tell our audience what you do and why you're the best person to talk about sensor fusion?
Sure. Thank you. Yeah, I'm a senior robotics arena scientist here at MathWorks. I work at the Advanced Research and Technology Office. And besides doing research, we also engage collaboration with academia, especially for research and development.
OK, awesome. So today, Roberto and I are going to introduce you to a new Toolbox that we released with Matlab 2018b. So Roberto, do you want to go ahead and tell us what this new toolbox is and what are the functionalities of it?
OK. So yes, the sensor fusion and tracking toolbox is a new toolbox that provides you features to fuse data from different kinds of sensors all together. And for example, here, as you can see in the slide, we fuse data from sensors as well as output from detection algorithms to have your robot, your vehicle, this is a self and situational awareness.
OK.
So we can describe this toolbox as the bridge between signal and image processing and your control part of your system.
Interesting. So it's basically making sense of your sensor data, right?
Yeah.
For lack of a better word.
Yeah, it makes sense.
OK, cool. So can you tell us a little bit more about what functionality does this toolbox contain?
Yeah. So among all the functionalities, it contains, for example, scenario and sensor simulation so you can simulate your sensors easily just using some function that is already provided by the toolbox, as well as tracking and localization algorithms.
OK.
You can also visualize your data or, for example, your path-- the path of your algorithm or robot. And eventually, if you want you can deploy the code that is being automatically generated by Matlab into your target, which can be a microcontroller or anything that is embedded in your robot.
OK. Cool. For today's agenda, Roberto is going to go through what an inertial measurement unit is. And then we're also going to talk about what a magnetic angular rate and gravity sensor is. So these are pretty common sensors in autonomous vehicles, in robots, just basically trying to orient yourself with the environment.
Then you want to go into what orientation estimation is. And we're going to do that for an IMU. We've got a pretty cool demo lined up. And then we're going to talk about some more sensor fusion for orientation estimation. So Roberto, why don't you take it away, and all the best.
yeah Thank you. Absolutely. So yes, Connell was saying here. So one of the functionalities of the newer sensor fusion and tracking toolbox is the orientation estimation. So you can actually get the orientation estimation without writing any complex Kalman filters or any other algorithm, but just by calling a function. That's the great thing about this toolbox.
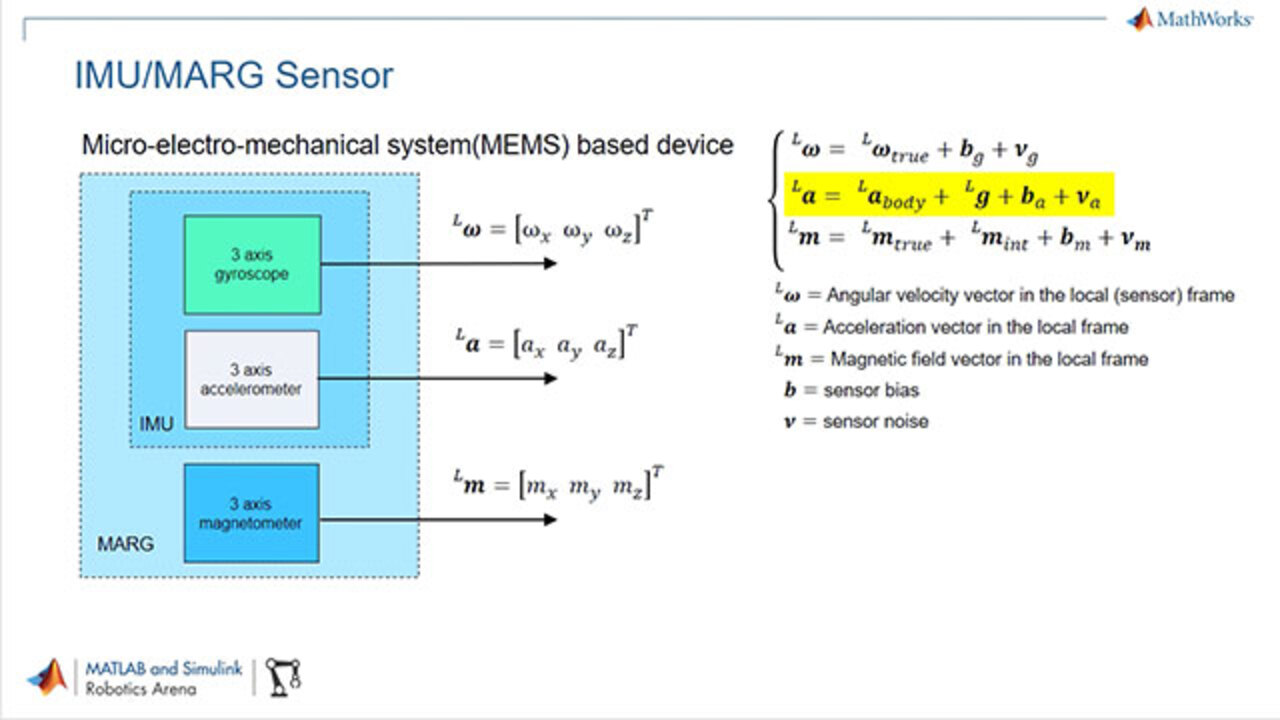
So OK, so let me tell a little bit about this sensor, si IMU and MARG. So an IMU, which stands for Inertial Measurement Unit, is a sensor that is composed of three axis gyroscope, which provides you a measurement of angular velocity in the three axis, x, y and z. Also, there is an accelerometer, 3 axis accelerometer for acceleration, of course. And if we have a magnetometer, which is basically a compass, a 3 axis compass, we usually refer to as MARG which stands for Magnetic Angular Rate and Gravity.
OK.
All right. So these sensors, if we want to deploy it on a robot or a small vehicle, we usually use the microelectromechanical system based devices, which are very small, cheap, very convenient. However, their accuracy is not that great. So there is noise. So that's why we model the output of the sensor as here described in the slides.
So on the right, you can see the angular velocity that we get from the sensor is composed of the true angular velocity plus we have bias and noise So the noise, as you know, is the high frequency noise that we have in any kind of sensor. And the bias is some sort of low frequency noise. We can consider it as a constant bias, like in a small window of time, right? So that's what we have.
Similarly, for the acceleration, we still have bias and noise. But we also have the true acceleration due to the motion, that I usually call it non-gravitational acceleration because it's the one due only to the motion of the vehicle, plus the gravity. So we actually have both, linear acceleration from the motion plus the gravity acceleration.
So in the case of a magnetometer, still bias noise plus the true magnetic field, which is, in this case, the Earth magnetic field. That's the one we need for orient ourselves, right? Especially for the heading. But we also have some magnetic disturbances. That's what I call int, the interference.
OK, cool.
Yeah. So from an IMU, we can estimate the orientation, as we said before, right? So an intuitive way to estimate the orientation might be just by integrating the angular velocities, right? So just simple integration, you get the three angles, roll, pitch, and yaw. However, as I was mentioning before, we have this bias. So as we integrate the output will be drifting-- so we're going to have a big error that is going to increase unbounded. So that's a big issue with just integrating angular velocity.
OK.
So yeah, you can also get an estimation from the accelerometer. The way we do it is basically by getting the measurement from the accelerometer, assuming there is no motion of the body. So basically there is no linear acceleration. But the only acceleration we measure is the gravity that is divided by the three components-- into the three components. Then we just use some trigonometry, we can get the rolling pitch with respect to the vertical, right? Vertical axis.
OK.
Because that's our gravity. Gravity always points down. However, as I was saying before, we only have roll, pitch, not yaw. The reason why we don't have the yaw is because any variation-- so basically the yaw-- doesn't give you any variation with respect to respect to the z-axis. So that's why we cannot use accelerometer for yaw.
However, yes, in this case, besides not having the yaw estimation, we also have a very nice estimation because the accelerometer has a high frequency noise, right? So the idea would be to get the best out of the two kind of estimations. So having something-- some estimation which doesn't have a lot of noise, but at the same time doesn't drift.
Correct. Correct.
So the first one, the estimation from the gyroscope, it's pretty smooth but drift, while the accelerometer is quite of the opposite. It doesn't drift but it has a lot of high frequency noise.
OK. So here, in the case of the magnetometer, so the magnetometer is usually used to correct the yaw, right? So as I was saying before, from the accelerometer we can only estimate rolling pitch. So the magnetometer would be a perfect sensor to get an estimation of the yaw. So usually, if we just use accelerometer magnetometer, we get the estimation roll and pitch to project the magnetic field vector into the horizontal plane. And then we get the heading of the magnetic field vector with respect to the global magnetic field vector.
OK. Makes sense.
But again, even in this case, we still have noise estimation. As I was saying before, the best way to do it is fuse together all these sensors to have a better orientation estimation, drift free and noise free. Ideal.
OK. So there are several methods to do that. So one of these methods, which is basically the most common and probably the best, is a Kalman filter. So from the Kalman filter you need a prediction step. So the first step would be getting the data from your input, get an estimate through a mathematical model, and then correct the estimation with some other measurement that would be, in this case, your correction. So we have two steps, prediction and correction.
In the case of orientation estimation from IMU, you get your prediction by integrating-- well, it's a bit more complicated than that, but we can assume it's just a simple integration of gyroscope readings. And then we correct by using the measurements from accelerometer and magnetometer.
So I see a few sigma values in there. Can you explain that?
Yes. Yes. The fusion that happens in the Kalman filter is a probabilistic fusion. So it's a probabilistic method to fuse this data together and based on maximum likelihood. So we need to have an estimation of the covariance of these measurements.
OK.
Or we can say, more generally, uncertainty of the readings.
So this is a value that you can get from a sensor data sheet.
Yes. Yes. Yes. So the sigma actually is just the standard deviation.
OK.
Then we square it and then we get the covariance.
All right. So we're going to go into Matlab real quick, and Roberto has put together a real cool demo. So I'm going to hand it over back to him.
Yeah. Sure. Yeah, so for this demo, I actually use the data from my iPhone over here. So it's an easy way to get data from an IMU because everyone has a phone. So from a phone using in our Matlab Mobile application, we can transfer this data to the Matlab in my desktop.
OK, now I have my phone. So the phone is going to stream data to the desktop application using the Matlab Mobile app. And OK, so here, this is the live script. This is my phone. So let me step through all the section of this live script. So first, as I said, it will connect my phone to the desktop Matlab.
And then OK, so here, here, basically, we define the iPhone object that basically is the object that will log the data from the phone's IMU. And then I will use this data to run the sensor fusion function.
OK, cool. So let's give the script a run and see what happens.
Yes. Of course. OK, so we run it. And then OK, then we stream in data. So I'm moving the phone around so you will see the orientation will change. OK. So it's done. So it did just a few seconds. And then the sensor fusion used the data that I just logged into the Matlab desktop, and it will calculate the orientation.
So in this case, I'm using the IMU filter function. The IMU filter function-- so let me just go back here. So the IMU filter function uses only accelerometer angular velocity. So we use internally indirect quaternion-based Kalman filter, extended Kalman filter. So the angular velocity, again, is used for prediction and the acceleration for correction.
However, as I said before, we don't have an orientation-- sorry, we don't have a correction for the yaw. So the yaw will just be from the angular velocity. So that's why we might see some drift.
OK. And again, the function that you use to declare the IMU filter, that function is part of the sensor fusion and tracking toolbox?
Yes. Yes. Absolutely. Yes.
OK.
So you can see how easy it is. So you just define your IMU filter here, just this line of code. And you give as input the sample rate. So in this case is the same sample rate--
As the iPhone?
As the iPhone, correct. And then you just need to give as input some parameters. So these are the covariances that I was talking about before, right? So we have the parameters, the covariance for the gyroscope, acceleration, right, and this linear acceleration noise is basically to mitigate the error due to the non-gravitational acceleration. OK, so when you actually move, like you shake your phone, in this case.
And this is the actual orientation estimation. So this, basically it's used to pass the data. So these are the input, acceleration, angular velocity. And this is the actual fusion. So the fusion happened here.
OK. Cool.
OK. And so along with the IMU data, so angular velocity, acceleration, I also stream the orientation from the iPhone. So inside the iPhone there is also an algorithm that estimates the orientation. So I'm streaming that data as well so we can compare our method with the one that is inside the iPhone.
So as you can see here-- so this is the role. Oh, by the way, let me just tell you that the sensor fusion that I'm using here does everything using quaternion. But just for the sake of simplicity, I'm converting it in roll, pitch, and yaw, so angles so we can simply visualize it.
So this is the roll. I can open this. So yeah as you can see, they are very close to each other. Of course, there is some difference because they are not the same by most likely--
The algorithms are different?
Algorithms are different, yes. OK. So this is roll and here is the pitch. So even in this case, of course, there is some difference.
Yeah. So what I can see is if I'm just analyzing this plot a little bit, I can see that at the start of your logging signal, you can see there is a larger difference between the two lines, but it sort of tends to converge after that. Is there a particular reason for that?
Yes, yes. OK, that's a good question. So the iPhone orientation estimation has been running for a while, most likely since this one was on, right?
Yeah, yeah.
So all the data, all the covariance, matrices, and so on, bias estimation, they all converged Because they need some time to converge to the proper value. So for the iPhone algorithm, most likely everything is converged While for our case, it may take some time because we run the algorithm as soon as we run the script. So of course, they are not settled.
That makes sense.
And eventually, I mean finally, we have yaw.
And this is the yaw, OK.
Yeah. So this is the yaw. And as I said before, we don't have correction from the magnetometer. But you don't see a lot of drift because this was run only for a few seconds. So they are still pretty close to each other.
OK, cool.
OK, so next we are going to show the filter with the magnetometer input. So magnetic field in this case would also be used in the sensor fusion. So the sensor fusion is still the same kind of algorithm. It's indirect extended Kalman filter, quaternion based, but again--
It's going to also take into account the magnetic--
Yes. In this case, yes, it does that. And also, a good thing about this filter that also estimates the magnetic disturbances. So it can mitigate the effect of the interference--
Interesting.
--that we have.
And that's actually a very interesting problem for these robot teams because usually, because the size of these robots are so tiny, the motors and actuators on these robots are usually very close to the IMU sensor, and that creates a lot of magnetic disturbance, more than anything else with the sensors. OK.
So yeah. Again, it's the same kind of algorithm. So we are going to use the same font, of course, the same kind of data, but with the add of the magnetic field for the orientation. OK, yeah. So if we run the filter and we just collect some data over here-- OK, so we will see the visualization, the output. OK.
So yeah, this is the role. And again, in this case, they look very close to each other. And yeah, this is--
You can see that error at the start.
Yeah, exactly. And then it will converge. So they will look much closer later on. And yeah, same thing for pitch. So in this case, the error at the beginning might be even bigger because we also have magnetic disturbance estimation. So it will take some time to converge. And yeah, and yaw.
OK.
Same thing.
That's cool. So how is calling the function for-- with the magnetometer correction different from the one that you showed us earlier? Is the function called the same as it's still just one single line of code that you can use?
Yeah. So the function is, in this case, called AHRS.
OK. So HHRS, yeah, that's a pretty common filter.
Yes, exactly. So AHRS basically stands for an Attitude and Heading Reference System.
Correct, correct.
Because well, in this case, we also have the heading reference system as well from magnetometer. Yeah. And it's in here.
OK. So the call signature is similar. You still feed in those additional parameters and then you--
Right. You have additional parameters for the magnetic field. And of course, the filter itself, you also have as input.
You also feed in the magnetic--
The magnetic field, yes.
OK, perfect.
Cool. So now let's go back to the slides. All right. So what are some few takeaways from here. So we can get an orientation estimation in just one function call. I mean, of course, there is some definition at the beginning, but all we have to do is just define the filter and call it-- feed the inputs. And the orientation estimated through an extended Kalman filter, so as I was saying before, it's an indirect quaternion based extended Kalman filter.
And the cool thing about this is that supports function and supports code generation. So we can just click a button and get C++ version of it.
Speaking of code generation, we just released a training on generating C and C++ code from Matlab and Simulink that you guys might want to check out. It's about it's about 4 or 5 hours of training material that you can go through at your own pace and you can download files. So once you figured out how to do that, you can take these functions and generate code for them as well.
OK. Awesome. Well, thank you so much, Roberto, for taking the time out to give us this presentation. Finally, before we wrap up, I just wanted to point you guys to the resources. You can get in touch with us either on Facebook or through our email address, and also check out the other links that we have up on screen. There's something for everyone over there. Thank you so much, and we hope to see you again on the Robotics Arena.