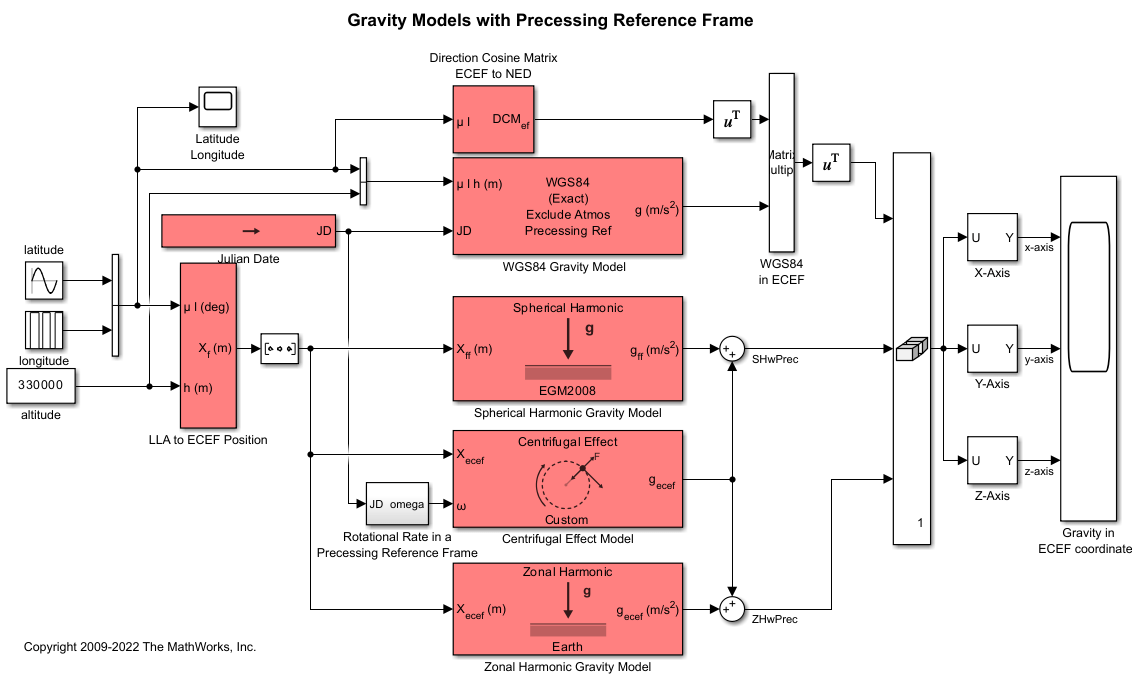
Direction Cosine Matrix ECEF to NED
Convert geodetic latitude and longitude to direction cosine matrix
Libraries:
Aerospace Blockset /
Utilities /
Axes Transformations
Description
The Direction Cosine Matrix ECEF to NED block converts geodetic latitude and longitude into a 3-by-3 direction cosine matrix (DCM). The DCM matrix performs the coordinate transformation of a vector in Earth-centered Earth-fixed (ECEF) axes into a vector in north-east-down (NED) axes. For more information on the direction cosine matrix, see Algorithms.
The implementation of the ECEF coordinate system assumes that the origin is at the center of the planet, the x-axis intersects the Greenwich meridian and the equator, the z-axis is the mean spin axis of the planet, positive to the north, and the y-axis completes the right-hand system. For more information, see About Aerospace Coordinate Systems.
Ports
Input
Output
Algorithms
The DCM matrix performs the coordinate transformation of a vector in ECEF axes, (ox0, oy0, oz0), into a vector in NED axes, (ox2, oy2, oz2). The order of the axis rotations required to bring this about is:
A rotation about oz0 through the longitude (ι) to axes (ox1, oy1, oz1)
A rotation about oy1 through the geodetic latitude (μ) to axes (ox2, oy2, oz2)
Combining the two axis transformation matrices defines the following DCM.
References
[1] Stevens, B. L., and F. L. Lewis. Aircraft Control and Simulation, Hoboken, NJ: John Wiley & Sons, 1992.
[2] Zipfel, Peter H., Modeling and Simulation of Aerospace Vehicle Dynamics. Second Edition. Reston, VA: AIAA Education Series, 2000.
[3] Recommended Practice for Atmospheric and Space Flight Vehicle Coordinate Systems, R-004-1992, ANSI/AIAA, February 1992.
Extended Capabilities
Version History
Introduced before R2006a