Normal Behavior

MATLAB's function rand(m,n) generates an m-by-n matrix with elements drawn from a uniform distribution, while randn(m,n) generates a matrix with normally or Gaussian distributed elements. We described the algorithm that MATLAB uses for uniform distributions five years ago in this newsletter. Now it's time to describe algorithms for normal distributions.

Almost all algorithms for generating normally distributed random numbers are based on transformations of uniform distributions. The simplest way to generate an m-by-n matrix with approximately normally distributed elements is to use the expression

sum(rand(m,n,12),3) - 6

This works because R = rand(m,n,p) generates a three-dimensional uniformly distributed array and sum(R,3) sums along the third dimension. The result is a two-dimensional array with elements drawn from a distribution with mean p/2 and variance p/12 that approaches a normal distribution as p increases. If we take p = 12, we get a pretty good approximation to the normal distribution and we get the variance to be equal to one without any additional scaling. There are two difficulties with this approach. It requires twelve uniforms to generate one normal, so it is slow. And the finite p approximation causes it to have poor behavior in the tails of the distribution.

Older versions of MATLAB - before MATLAB 5 - used the polar algorithm. This generates two values at a time. It involves finding a random point in the unit circle by generating uniformly distributed points in the [0,1]x[0,1] square and rejecting any points outside of the circle. Points in the square are represented by vectors with two components. The rejection portion of the code is:

r = 2;
while r > 1
   u = 2*rand(2,1)-1
   r = u'*u
end

For each point accepted, the polar transformation

v = sqrt(-2*log(r)/r)*u

produces a vector with two independent normally distributed elements. This algorithm does not involve any approximations, so it has the proper behavior in the tails of the distribution. But it is moderately expensive. Over 21% of the uniform numbers are rejected when they fall outside of the circle and the square root and logarithm calculations contribute significantly to the cost.

Beginning with MATLAB 5, and continuing with MATLAB 6, randn uses a sophisticated table lookup algorithm developed by George Marsaglia of Florida State University. Marsaglia calls his approach the "ziggurat" algorithm. Ziggurats are ancient Mesopotamian terraced temple mounds that, mathematically, are two-dimensional step functions. A one-dimensional ziggurat underlies Marsaglia's algorithm.

Marsaglia has refined his ziggurat algorithm over the years. An early version is described in Knuth's classic The Art of Computer Programming, volume II. MATLAB's version is described by Marsaglia and W. W. Tsang in the SIAM Journal of Scientific and Statistical Programming, volume 5, 1984. A Fortran subroutine is discussed briefly in the Kahaner, Moler, and Nash text book, Numerical Methods and Software, and is available from the MathWorks FTP site. A recent version is available in the online electronic journal, Journal of Statistical Software. We describe this recent version here because it is the most elegant. The version actually used in MATLAB is more complicated, but is based on the same ideas and is just as effective.

The probability density function, or pdf, of the normal distribution is the bell-shaped curve
F(x) = c exp(-x²/2)

where c=1/(2π)^1/2 is a normalizing constant that we can ignore. If we generate random points (x,y), uniformly distributed in the plane, and reject all of them that do not fall under this curve, the remaining x's form our desired normal distribution.

The ziggurat algorithm covers the area under the pdf by a slightly larger area with n sections. The accompanying picture has n = 8; the actual code uses n = 128. The ziggurat is shown in solid blue. The top n-1 sections are rectangles. The bottom section is a rectangle together with an infinite tail under the graph of F(x). The right-hand edges of the rectangles are at the points x_k,k=2,...,n, shown with circles in the picture. With f(x₁) = 1 and f(x_n+1) = 0 and the height of the k-th section is F(x_k) - F(x_k+1). The key idea is to choose the x_ks so that all n sections, including the unbounded one on the bottom, have the same area. There are other algorithms that approximate the area under the pdf with rectangles. The distinguishing features of Marsaglia's algorithm are the facts that the rectangles are horizontal and have equal areas.

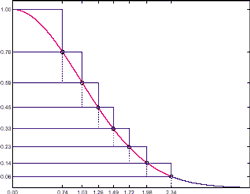
For a specified number, n, of sections, it is possible to solve a transcendental equation to find x_k, the point where the infinite tail meets the first rectangular section. In our picture with n = 8, it turns out that x_n = 2.34. In the actual code with n = 128, x_n = 3.4426. Once x_n is known, it is easy to compute the common area of the sections and the other right-hand end points, x_k. It is also possible to compute σ_k=x_k-1/x_k, the fraction of each section that lies underneath the section above it. Let's call these fractional sections the "core" of the ziggurat. The right-hand edge of the core is the dotted blue line in our picture. The computation of these x_k's and σ_k's is done in an initialization section of code that is run only once in any MATLAB session.

After the initialization, normally distributed random numbers can be computed very quickly. The key portion of the code computes a single random integer, k, between 1 and n, and a single uniformly distributed random number, u, between -1 and 1. A check is then made to see if u falls in the core of the k-th section. If it does, then we know that ux_k is the x-coordinate of a point under the pdf and this value can be returned as one sample from the normal distribution. The code looks something like this. (In the actual built-in function, a fast shift-register generator computes the random integer.)

k = ceil(128*rand);
u = 2*rand-1;
if abs(u) < sigma(k)
   v = u*x(k);
   return
end

Most of the σ_k's are greater than 0.98, and the test is true over 97% of the time. One normal random number can usually be computed from one random integer, one random uniform, an if-test and a multiplication. No square roots or logarithms are required.

The point determined by k and u will fall outside of the core less than 3% of the time. This happens when k= 1 because the top section has no core, when k is between 2 and n-1 and the random point is in one of the little rectangles covering the graph of F(x), or when k = n and the point is in the infinite tail. In these cases, additional computations involving logarithms, exponentials and more uniform samples are required.

It is important to realize that, even though the ziggurat step function only approximates the probability density function, the resulting distribution is exactly normal. Decreasing n decreases the amount of storage required for the tables and increases the fraction of time that extra computation is required, but does not affect the accuracy. Even with n = 8, we would have to do the more costly corrections almost 23% of the time, instead of less than 3%, but we would still get an exact normal distribution.

With this algorithm, MATLAB 6 can generate normally distributed random numbers as fast as it can generate uniformly distributed ones. In fact, MATLAB on my 800 MHz Pentium III laptop can generate over 10 million random numbers from either distribution in less than one second.

MATLAB's built-in function randn uses two unsigned 32-bit integers, one for the seed in the uniform generator and one as the shift register for the integer generator. The code that processes points outside the core of the ziggurat accesses these two generators independently, so the period of the overall generator is 2⁶⁴. At 10 million normal deviates per second, randn will take over 58,000 years before it repeats.