Generate Single-Precision MATLAB Code
This example shows how to generate single-precision MATLAB® code from double-precision MATLAB code. This example shows the single-precision conversion workflow that you use when you want to see single-precision MATLAB code or use verification options. Optionally, you can also generate single-precision C/C++ code.
Prerequisites
To complete this example, install the following products:
MATLAB
MATLAB Coder™
Fixed-Point Designer™
C compiler
See Supported Compilers.
You can use
mex -setupto change the default compiler. See Change Default Compiler.
Create a Folder and Copy Relevant Files
In a local, writable folder, create a function
ex_2ndOrder_filter.m.function y = ex_2ndOrder_filter(x) %#codegen persistent z if isempty(z) z = zeros(2,1); end % [b,a] = butter(2, 0.25) b = [0.0976310729378175, 0.195262145875635, 0.0976310729378175]; a = [1, -0.942809041582063, 0.3333333333333333]; y = zeros(size(x)); for i = 1:length(x) y(i) = b(1)*x(i) + z(1); z(1) = b(2)*x(i) + z(2) - a(2) * y(i); z(2) = b(3)*x(i) - a(3) * y(i); end end
Create a test file,
ex_2ndOrder_filter_test.m, to exercise theex_2ndOrder_filteralgorithm.It is a best practice to create a separate test script for preprocessing and postprocessing such as:
Setting up input values.
Calling the function under test.
Outputting the test results.
To cover the full intended operating range of the system, the test script runs the
ex_2ndOrder_filterfunction with three input signals: chirp, step, and impulse. The script then plots the outputs.% ex_2ndOrder_filter_test % % Define representative inputs N = 256; % Number of points t = linspace(0,1,N); % Time vector from 0 to 1 second f1 = N/2; % Target frequency of chirp set to Nyquist x_chirp = sin(pi*f1*t.^2); % Linear chirp from 0 to Fs/2 Hz in 1 second x_step = ones(1,N); % Step x_impulse = zeros(1,N); % Impulse x_impulse(1) = 1; % Run the function under test x = [x_chirp;x_step;x_impulse]; y = zeros(size(x)); for i = 1:size(x,1) y(i,:) = ex_2ndOrder_filter(x(i,:)); end % Plot the results titles = {'Chirp','Step','Impulse'} clf for i = 1:size(x,1) subplot(size(x,1),1,i) plot(t,x(i,:),t,y(i,:)) title(titles{i}) legend('Input','Output') end xlabel('Time (s)') figure(gcf) disp('Test complete.')
| Type | Name | Description |
|---|---|---|
| Function code | ex_2ndOrder_filter.m | Entry-point MATLAB function |
| Test file | ex_2ndOrder_filter_test.m | MATLAB script that tests
|
Set Up the Single-Precision Configuration Object
Create a single-precision configuration object. Specify the test file name. Verify the single-precision code using the test file. Plot the error between the double-precision code and single-precision code. Use the default values for the other properties.
scfg = coder.config('single'); scfg.TestBenchName = 'ex_2ndOrder_filter_test'; scfg.TestNumerics = true; scfg.LogIOForComparisonPlotting = true;
Generate Single-Precision MATLAB Code
To convert the double-precision MATLAB function, ex_2ndOrder_filter,
to single-precision MATLAB code, use the codegen function with the -double2single option.
codegen -double2single scfg ex_2ndOrder_filter
codegen analyzes the double-precision
code. The conversion process infers types by running the test file
because you did not specify the input types for the ex_2ndOrder_filter function.
The conversion process selects single-precision types for the double-precision
variables. It selects int32 for index variables.
When the conversion is complete, codegen generates a type
proposal report.
View the Type Proposal Report
To see the types that the conversion process selected for the
variables, open the type proposal report for the ex_2ndOrder_filter function.
Click the link ex_2ndOrder_filter_report.html.
The report opens in a web browser. The conversion process converted:
Double-precision variables to
single.The index
itoint32. The conversion process casts index and dimension variables toint32.

View Generated Single-Precision MATLAB Code
To view the report for the generation of the single-precision MATLAB code, in the Command Window:
Scroll to the Generate Single-Precision Code step. Click the View report link.
In the MATLAB Source pane, click
ex_2ndOrder_filter_single.
The code generation report displays the single-precision MATLAB code
for ex_2ndOrder_filter.
View Potential Data Type Issues
When you generate single-precision code, codegen enables highlighting of potential
data type issues in code generation reports. If codegen cannot remove a double-precision
operation, the report highlights the MATLAB expression that results in the operation. Click the Code
Insights tab. The absence of potential data type issues indicates that
no double-precision operations remain.
Compare the Double-Precision and Single-Precision Variables
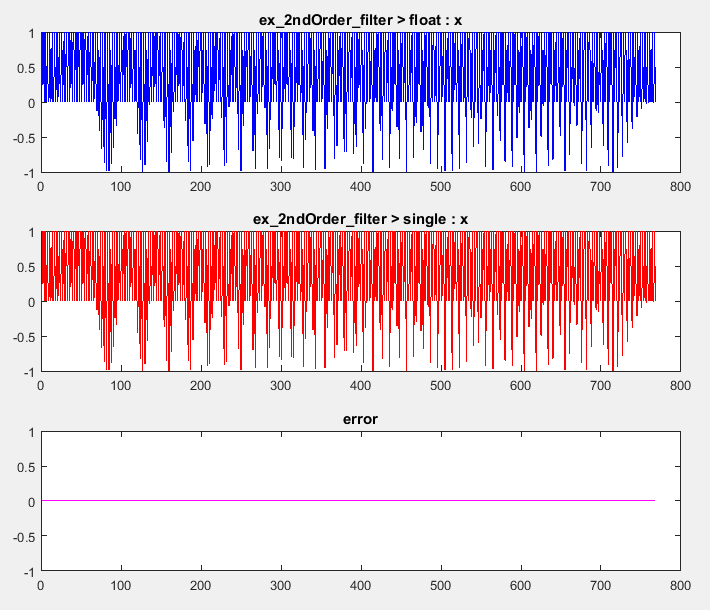
You can see the comparison plots for the input x and output
y because you selected to log inputs and outputs for comparison plots.

Optionally Generate Single-Precision C Code
If you also want to generate single-precision C code, create
a code configuration object for C code generation. Use this configuration
object with the -config option of the codegen function.
For example:
Create a code configuration object for generation of a C static library.
cfg = coder.config('lib');Generate the C code. Enable generation of the code generation report.
codegen -double2single scfg -config cfg ex_2ndOrder_filter -report
To view the code generation report for the C code generation, click the View Report link.
In the Generated Code pane, click
ex_2ndOrder_filter.c.Double-precision variables have type
floatin the C code.The index
iis an integer.
When you generate single-precision code,
codegenenables highlighting of potential data type issues in the code generation report. Ifcodegencannot remove a double-precision operation, the report highlights the MATLAB expression that results in the operation.Click the Code Insights tab. Then, expand Potential data type issues. The absence of double-precision operations indicates that no double-precision operations remain.
See Also
coder.SingleConfig | codegen | coder.config