Estimate Direction of Arrival Using MUSIC Algorithm and TwinRX Daughterboard
This example shows how to estimate the direction of arrival of a signal with the multiple signal classification (MUSIC) algorithm and a X300/X310 USRP™ radio with TwinRX daughterboards. In this example, you capture the signal from a transmitter and apply the MUSIC algorithm to estimate the direction from which the signal arrives. This example requires two MATLAB™ sessions, one for transmitter and one for the receiver. In one MATLAB session, you run the transmitter script to transmit a 10 kHz signal, and in another MATLAB session, you run the DOA estimation example to calculate the direction of arrival.
Required Hardware and Software
To run this example, you require:
300-Series USRP radio (X3xx) with two TwinRX daughterboards and Wireless Testbench Support Package for NI USRP Radios. For information on mapping an NI USRP device to an Ettus Research 300-series USRP device, see Supported Radio Devices (Wireless Testbench).
200-Series USRP radio (B2xx or N2xx) and Communications Toolbox Support Package for USRP Radio, required when using the radio as the transmitter. For information on mapping an NI™ USRP device to an Ettus Research 200-series USRP device, see Supported Hardware and Required Software.
Phased Array System toolbox
Five antennas and suitable connecting cables of equal length
One 4-way power splitter or three 2-way power splitters
Introduction to Direction of Arrival Estimation
Direction of arrival (DOA) estimation involves determining the direction from which a received signal originates relative to the receiver antenna array. This process has applications in tracking moving objects, localizing signal sources, and beamforming.
The MUSIC algorithm is a method for estimating the direction of arrival of signals. It is based on the eigenstructure of the covariance matrix derived from the antenna array data. The MUSIC algorithm exploits the orthogonality between the signal subspace and the noise subspace to determine the DOA. For more information on the MUSIC algorithm, see phased.MUSICEstimator (Phased Array System Toolbox). The angle estimation process consists of two steps.
1.Phase calibration between the four channels of X3xx radio: You connect the signal transmit source to all four receiving channels using a power splitter so that you can measure and correct phase offset between the channels.
2. Estimation of direction of arrival: You connect the four receiver channels to a four-channel antenna array and estimate the direction of arrival. To find the direction of arrival of a signal, the example uses a phased.MUSICEstimator (Phased Array System Toolbox) System object. The phased.MUSICEstimator System object implements the spatial spectrum of the incoming signal by using a narrowband MUSIC beamformer for a uniform linear array (ULA).
Setup
This example requires Phased Array System Toolbox. Before running the example, perform these steps:
Configure your host computer to work with a 300-Series USRP Radio (X3xx) and Wireless Testbench Support Package for NI USRP Radios.
If you are using a 200-Series USRP Radio (B2xx or N2xx) as the transmit signal source, you must also configure your host computer to work with the Communications Toolbox Support Package for USRP Radio.
Make sure that you have both the transmitter script
sdruDOAExampleTransmitter.mlxand receiver scriptDirectionOfArrivalEstimationUsingTwinRXExample.mlx. open, with each configured to run on its own SDR hardware in its own instance of MATLAB.For calibration at the receiver side, connect the power splitter from the transmitter to the four receiver channels of the X3xx radio.
For DOA estimation, set up a linear antenna array of four antennas with adjacent antennas at a distance of lambda/2. Since we are using a center frequency of 2.4 GHz, a spacing of 6.25 cm is required between two adjacent antennas.
Transmit and Capture RF Signal
In one MATLAB session, you run the sdruDOAExampleTransmitter.mlx script to transmit an RF signal.
In the second MATLAB session, you run this example to capture the transmitted RF signal.
Create a comm.SDRuReceiver System object and set the IP address, center frequency, and receiver gain.
radioAddress ='192.168.40.2'; centerFrequency =
2400000000; gain =
60; radio = sdruDOAEstimationReceiver_init(radioAddress, centerFrequency, gain);
Checking radio connections...
% Angles by which each channel needs to be rotated angle1 = 0; angle2 = 0; angle3 = 0; ToneFrequency = 10e3; timeCounter = 0; % seconds radioFrameTime = (radio.SamplesPerFrame * radio.DecimationFactor / radio.MasterClockRate); % seconds
Create a spectrumAnalyzer and timescope System objects to visualize the received signal in the frequency and time domains, respectively.
spectrumScope = spectrumAnalyzer('SampleRate', radio.MasterClockRate/radio.DecimationFactor); timeScope = timescope('TimeSpan',4/ToneFrequency,'SampleRate',radio.MasterClockRate/radio.DecimationFactor);
To find the direction of arrival of a signal, use the phased.MUSICEstimator System object.
lambda = physconst('LightSpeed')/radio.CenterFrequency; array = phased.ULA('NumElements',4,'ElementSpacing',lambda/2); estimator = phased.MUSICEstimator('SensorArray',array,... 'OperatingFrequency',radio.CenterFrequency,'ForwardBackwardAveraging',true,... 'DOAOutputPort',true,'NumSignalsSource','Property',... 'NumSignals',1,'SpatialSmoothing',1);
Estimate and Correct Phase Offset
You run the sdruDOAPhaseCalibration.m function to estimate and correct the phase offset between all the receiver channels.
CalibrationTime = 1; % Time for which Phase Calibration is done
[angle1, angle2, angle3] = sdruDOAPhaseCalibration(radio, CalibrationTime, radioFrameTime);

Connect Antenna Array
To change the connections, follow these steps:
Disconnect the power splitter connecting the transmitter and receiver without powering off the board. Then, use SMA cables of equal length to connect the four channels of the X3xx radio to the antenna array.
Connect the USRP radio transmitter port to an antenna.
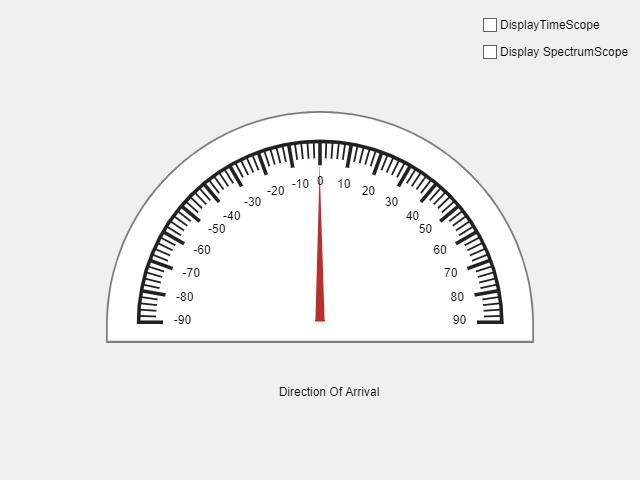
You can now move the transmitting antenna and see the corresponding change in the arrival angle on the semicircular gauge.
disp("Remove the power splitter and connect to the antenna array for DOA estimation");Please Remove the Power splitter and connect to the antenna array for DOA Estimation
Display Direction of Arrival
Use the sdruDOAEstimationApp.mlapp app to display the direction of arrival of the transmitted signal and to display the time and frequency plots of the received signal. Select the Display TimeScope or Display SpectrumScope check box to monitor power and the frequency of the signal received by the antenna array.
app = []; if isempty(app) app = sdruDOAEstimationApp(); end
Set the simulation to capture 1000 seconds of data.
StopTime = 1000; % Time to stop the simulation in secondsEstimate Angle of Arrival
Connect the [1 2 3 4] receiver channels of the X3xx radio to the antennas in the antenna array from left to right.
try % Loop until the timeCounter reaches the target stop time. while (timeCounter < StopTime) [data, valid, overrun] = radio(); if ~overrun data = sdruDOAEstimationAmplitudeNormalization(data); % Rotating IQ data data = sdruDOAEstimationRotateIQ4Channels(data,angle1,angle2,angle3); % Calculating the direction of arrival [~,doas] = estimator(data); pause(1e-6); % Adding pause for UI Update % Display angle in UI if isscalar(doas) app.displayAngle(doas); end % Visualize in time domain if(app.DisplayTimeScopeCheckBox.Value) timeScope(data); dataMaxLimit = max(max(abs([real(data); imag(data)]))); timeScope.YLimits = [ -dataMaxLimit*1.5, dataMaxLimit*1.5 ]; end % Visualize frequency spectrum if(app.DisplaySpectrumScopeCheckBox.Value) spectrumScope(data); end timeCounter = timeCounter + radioFrameTime; end end catch ME release(radio); release(timeScope); release(spectrumScope); rethrow(ME); end

You can see the estimated direction of arrival angle in the semicircular gauge of the app.
Release the comm.SDRuReceiver and visualization scopes, and delete the app handle.
release(radio); release(timeScope); release(estimator); release(spectrumScope); delete(app);
Further Exploration
You can modify the transmitter script sdruDOAExampleTransmitter.mlx to create various waveforms and run the example to estimate the direction of arrival values accurately.
Troubleshooting
To avoid multipath reflections, test this example in an open environment. Hold the transmitting and receiving antenna array at the same elevation. If you are working in a closed space, keep the transmitter in the near field of the antenna array.
For proper reception of the signal, you may need to increase the gain of the transmitter object after connecting to the antenna array. To increase the gain, release the transmitter object, modifying
sdruDOAExampleTransmitter.mlxscriptsdruDOAExampleTransmitter.mlxagain.The MUSIC algorithm estimates the broadside angle (azimuth angle) only when the elevation angle is near zero. To get accurate DOA, ensure that the elevation angle is near zero
This example estimates the angle continuously from -70 to 70 degrees. When you move the transmitter beyond these limits, discontinuities appear in the estimated angle.
To increase the accuracy of the estimated DOA, you must calibrate the antenna array setup.