Radial Basis Neural Networks
Neuron Model
Here is a radial basis network with R inputs.
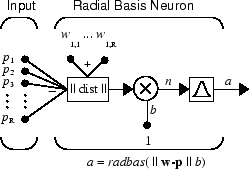
Notice that the expression for the net input of a radbas neuron is different from
that of other neurons. Here the net input to the radbas transfer function is the
vector distance between its weight vector w and
the input vector p, multiplied by the bias
b. (The ||
dist
|| box in this figure accepts the input vector p and the single row input weight matrix, and
produces the dot product of the two.)
The transfer function for a radial basis neuron is
Here is a plot of the radbas transfer function.
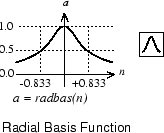
The radial basis function has a maximum of 1 when its input is 0. As the distance between w and p decreases, the output increases. Thus, a radial basis neuron acts as a detector that produces 1 whenever the input p is identical to its weight vector w.
The bias b allows the sensitivity of the radbas neuron to be adjusted.
For example, if a neuron had a bias of 0.1 it would output 0.5 for any input
vector p at vector distance of 8.326
(0.8326/b) from its weight vector w.
Network Architecture
Radial basis networks consist of two layers: a hidden radial basis layer of S1 neurons, and an output linear layer of S2 neurons.
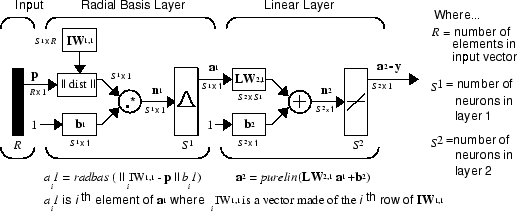
The ||
dist
|| box in this figure accepts the input vector p and the input weight matrix IW1,1, and produces a vector having
S1 elements. The elements are the
distances between the input vector and vectors
iIW1,1 formed from the rows of the
input weight matrix.
The bias vector b1
and the output of ||
dist
|| are combined with the MATLAB® operation .* , which does element-by-element
multiplication.
The output of the first layer for a feedforward network net
can be obtained with the following code:
a{1} = radbas(netprod(dist(net.IW{1,1},p),net.b{1}))
Fortunately, you won't have to write such lines of code. All the details of
designing this network are built into design functions newrbe and newrb, and you can obtain their
outputs with sim.
You can understand how this network behaves by following an input vector p through the network to the output a2. If you present an input vector to such a network, each neuron in the radial basis layer will output a value according to how close the input vector is to each neuron's weight vector.
Thus, radial basis neurons with weight vectors quite different from the input vector p have outputs near zero. These small outputs have only a negligible effect on the linear output neurons.
In contrast, a radial basis neuron with a weight vector close to the input vector p produces a value near 1. If a neuron has an output of 1, its output weights in the second layer pass their values to the linear neurons in the second layer.
In fact, if only one radial basis neuron had an output of 1, and all others had outputs of 0s (or very close to 0), the output of the linear layer would be the active neuron's output weights. This would, however, be an extreme case. Typically several neurons are always firing, to varying degrees.
Now look in detail at how the first layer operates. Each neuron's weighted
input is the distance between the input vector and its weight vector, calculated
with dist. Each neuron's net input is
the element-by-element product of its weighted input with its bias, calculated
with netprod. Each neuron's output is
its net input passed through radbas. If a neuron's weight
vector is equal to the input vector (transposed), its weighted input is 0, its
net input is 0, and its output is 1. If a neuron's weight vector is a distance
of spread from the input vector, its weighted input is
spread, its net input is sqrt(−log(.5)) (or 0.8326),
therefore its output is 0.5.
Exact Design (newrbe)
You can design radial basis networks with the function newrbe. This function can
produce a network with zero error on training vectors. It is called in the
following way:
net = newrbe(P,T,SPREAD)
The function newrbe takes matrices of input
vectors P and target vectors T, and a spread constant SPREAD for the radial basis
layer, and returns a network with weights and biases such that the outputs are
exactly T when the inputs are P.
This function newrbe creates as many radbas neurons as there are
input vectors in P, and sets the first-layer weights to
P'. Thus, there is a layer of radbas neurons in which each
neuron acts as a detector for a different input vector. If there are
Q input vectors, then there will be Q
neurons.
Each bias in the first layer is set to 0.8326/SPREAD. This
gives radial basis functions that cross 0.5 at weighted inputs of +/−
SPREAD. This determines the width of an area in the
input space to which each neuron responds. If SPREAD is 4,
then each radbas neuron will respond with
0.5 or more to any input vectors within a vector distance of 4 from their weight
vector. SPREAD should be large enough that neurons respond
strongly to overlapping regions of the input space.
The second-layer weights IW
2,1 (or in code,
IW{2,1}) and biases b2 (or in
code, b{2}) are found by simulating the first-layer outputs
a1 (A{1}), and then solving
the following linear expression:
[W{2,1} b{2}] * [A{1}; ones(1,Q)] = T
You know the inputs to the second layer (A{1}) and the
target (T), and the layer is linear. You can use the
following code to calculate the weights and biases of the second layer to
minimize the sum-squared error.
Wb = T/[A{1}; ones(1,Q)]
Here Wb contains both weights and biases, with the biases in
the last column. The sum-squared error is always 0, as explained below.
There is a problem with C constraints (input/target pairs)
and each neuron has C +1 variables (the C
weights from the C
radbas neurons, and a bias). A
linear problem with C constraints and more than
C variables has an infinite number of zero error
solutions.
Thus, newrbe creates a network with
zero error on training vectors. The only condition required is to make sure that
SPREAD is large enough that the active input regions of
the radbas neurons overlap enough so
that several radbas neurons always have
fairly large outputs at any given moment. This makes the network function
smoother and results in better generalization for new input vectors occurring
between input vectors used in the design. (However, SPREAD
should not be so large that each neuron is effectively responding in the same
large area of the input space.)
The drawback to newrbe is that it produces a
network with as many hidden neurons as there are input vectors. For this reason,
newrbe does not return an
acceptable solution when many input vectors are needed to properly define a
network, as is typically the case.
More Efficient Design (newrb)
The function newrb iteratively creates a radial basis network one neuron at a time. Neurons are added to the
network until the sum-squared error falls beneath an error goal or a maximum
number of neurons has been reached. The call for this function is
net = newrb(P,T,GOAL,SPREAD)
The function newrb takes matrices of input
and target vectors P and T, and design
parameters GOAL and SPREAD, and returns
the desired network.
The design method of newrb is similar to that of
newrbe. The difference is that
newrb creates neurons one at a
time. At each iteration the input vector that results in lowering the network
error the most is used to create a radbas neuron. The error of the
new network is checked, and if low enough newrb is finished. Otherwise the
next neuron is added. This procedure is repeated until the error goal is met or
the maximum number of neurons is reached.
As with newrbe, it is important that the
spread parameter be large enough that the radbas neurons respond to
overlapping regions of the input space, but not so large that all the neurons
respond in essentially the same manner.
Why not always use a radial basis network instead of a standard feedforward
network? Radial basis networks, even when designed efficiently with newrbe, tend to have many times
more neurons than a comparable feedforward network with tansig or logsig neurons in the hidden
layer.
This is because sigmoid neurons can have outputs over a large region of the
input space, while radbas neurons only respond to
relatively small regions of the input space. The result is that the larger the
input space (in terms of number of inputs, and the ranges those inputs vary
over) the more radbas neurons required.
On the other hand, designing a radial basis network often takes much less time than training a sigmoid/linear network, and can sometimes result in fewer neurons' being used, as can be seen in the next example.
Examples
The example Radial Basis Approximation shows how a radial basis network is used to fit a function. Here the problem is solved with only five neurons.
Examples Radial Basis Underlapping Neurons and Radial Basis Overlapping Neurons examine how the spread constant affects the design process for radial basis networks.
In Radial Basis Underlapping Neurons, a radial basis network is designed to solve the same problem as in Radial Basis Approximation. However, this time the spread constant used is 0.01. Thus, each radial basis neuron returns 0.5 or lower for any input vector with a distance of 0.01 or more from its weight vector.
Because the training inputs occur at intervals of 0.1, no two radial basis neurons have a strong output for any given input.
Radial Basis Underlapping Neurons showed that having too small a spread constant can result in a solution that does not generalize from the input/target vectors used in the design. Example Radial Basis Overlapping Neurons shows the opposite problem. If the spread constant is large enough, the radial basis neurons will output large values (near 1.0) for all the inputs used to design the network.
If all the radial basis neurons always output 1, any information presented to
the network becomes lost. No matter what the input, the second layer outputs
1's. The function newrb will attempt to find a
network, but cannot because of numerical problems that arise in this
situation.
The moral of the story is, choose a spread constant larger than the distance between adjacent input vectors, so as to get good generalization, but smaller than the distance across the whole input space.
For this problem that would mean picking a spread constant greater than 0.1, the interval between inputs, and less than 2, the distance between the leftmost and rightmost inputs.