firceqrip
Constrained equiripple FIR filter
Syntax
B = firceqrip(n,Fo,DEV)
B = firceqrip(...,'slope',r)
B = firceqrip('minorder',[Fp Fst],DEV)
B = firceqrip(...,'passedge')
B = firceqrip(...,'stopedge')
B = firceqrip(...,'high')
B = firceqrip(...,'min')
B = firceqrip(...,'invsinc',C)
B = firceqrip(...,'invdiric',C)
Description
B = firceqrip(n,Fo,DEV) designs
an order n filter (filter length equal n +
1) lowpass FIR filter with linear phase.
firceqrip produces the same equiripple
lowpass filters that firpm produces
using the Parks-McClellan algorithm. The difference is how you specify
the filter characteristics for the function.
The input argument Fo specifies the frequency
at the upper edge of the passband in normalized frequency (0<Fo<1).
The two-element vector dev specifies the peak or
maximum error allowed in the passband and stopbands. Enter [d1
d2] for dev where d1 sets
the passband error and d2 sets the stopband error.
B = firceqrip(...,'slope',r) uses
the input keyword 'slope' and input argument r to
design a filter with a nonequiripple stopband. r is
specified as a positive constant and determines the slope of the stopband
attenuation in dB/normalized frequency. Greater values of r result
in increased stopband attenuation in dB/normalized frequency.
B = firceqrip('minorder',[Fp Fst],DEV) designs filter with the
minimum number of coefficients required to meet the deviations in
DEV = [d1
d2] while having a transition width no greater than
Fst – Fp, the difference between the
stopband and passband edge frequencies. You can specify 'mineven'
or 'minodd' instead of 'minorder' to design
minimum even order (odd length) or minimum odd order (even length) filters,
respectively. The 'minorder' option does not apply when you specify
the 'min' (minimum-phase), 'invsinc', or the
'invdiric' options.
B = firceqrip(...,'passedge') designs
a filter where Fo specifies the frequency at which
the passband starts to rolloff.
B = firceqrip(...,'stopedge') designs
a filter where Fo specifies the frequency at which
the stopband begins.
B = firceqrip(...,'high') designs
a high pass FIR filter instead of a lowpass filter.
B = firceqrip(...,'min') designs
a minimum-phase filter.
B = firceqrip(...,'invsinc',C) designs
a lowpass filter whose magnitude response has the shape of an inverse
sinc function. This may be used to compensate for sinc-like responses
in the frequency domain such as the effect of the zero-order hold
in a D/A converter. The amount of compensation in the passband is
controlled by C, which is specified as a scalar
or two-element vector. The elements of C are specified
as follows:
If
Cis supplied as a real-valued scalar or the first element of a two-element vector,firceqripconstructs a filter with a magnitude response of 1/sinc(C*pi*F) whereFis the normalized frequency.If
Cis supplied as a two-element vector, the inverse-sinc shaped magnitude response is raised to the positive powerC(2). If we setP=C(2),firceqripconstructs a filter with a magnitude response 1/sinc(C*pi*F)P.
If this FIR filter is used with a cascaded integrator-comb (CIC)
filter, setting C(2) equal to the number of stages
compensates for the multiplicative effect of the successive sinc-like
responses of the CIC filters.
Note
Since the value of the inverse sinc function becomes unbounded at
C=1/F, the value of C should be greater
the reciprocal of the passband edge frequency. This can be expressed as
Fo<1/C. For users familiar with CIC decimators,
C is equal to 1/2 the product of the differential delay and
decimation factor.
B = firceqrip(...,'invdiric',C) designs a lowpass filter with a passband
that has the shape of an inverse Dirichlet sinc function. The frequency response of the
inverse Dirichlet sinc function is given by where C, r, and
p are scalars. The input C can be a scalar or
vector containing 2 or 3 elements. If C is a scalar,
p and r equal 1. If C is a
two-element vector, the first element is C and the second element is
p, [C p]. If C is a
three-element vector, the third element is r, [C p
r].
Examples
To introduce a few of the variations on FIR filters that you
design with firceqrip, these five examples cover
both the default syntax b = firceqrip(n,wo,del) and
some of the optional input arguments. For each example, the input
arguments n, wo, and del remain
the same.
Filter design using firceqrip
Design a 30th order FIR filter using firceqrip.
b = firceqrip(30,0.4,[0.05 0.03]); freqz(b)

Design a minimum order FIR filter using firceqrip. The passband edge and stopband edge frequencies are 0.35 and 0.45 rad/sample. The allowed deviations are 0.02 and 1e-4.
b = firceqrip('minorder',[0.35 0.45],[0.02 1e-4]);
freqz(b)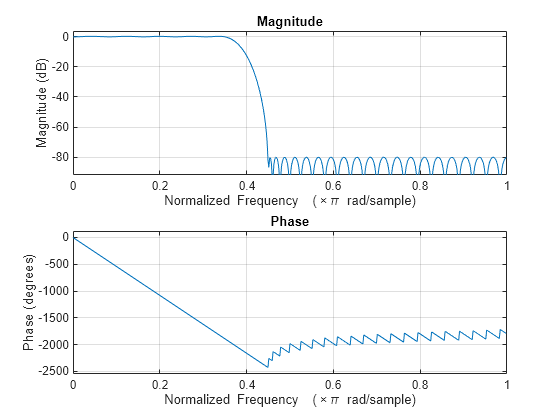
Design a 30th order FIR filter with the stopedge keyword to define the response at the edge of the filter stopband.
b = firceqrip(30,0.4,[0.05 0.03],'stopedge');
freqz(b)
Design a 30th order FIR filter with the slope keyword and r = 20.
b = firceqrip(30,0.4,[0.05 0.03],'slope',20,'stopedge'); freqz(b)

Design a 30th order FIR filter defining the stopband and specifying that the resulting filter is minimum phase with the min keyword.
b = firceqrip(30,0.4,[0.05 0.03],'stopedge','min'); freqz(b)

Comparing this filter to the filter in Figure 1. The cutoff frequency wo = 0.4 now applies to the edge of the stopband rather than the point at which the frequency response magnitude is 0.5.
Viewing the zero-pole plot shown here reveals this is a minimum phase FIR filter - the zeros lie on or inside the unit circle, z = 1
zplane(b)

Design a 30th order FIR filter with the invsinc keyword to shape the filter passband with an inverse sinc function.
b = firceqrip(30,0.4,[0.05 0.03],'invsinc',[2 1.5]);
freqz(b)
The inverse sinc function being applied is defined as 1/sinc(2*w)^1.5.
Inverse-Dirichlet-Sinc-Shaped Passband
Design two order 30 constrained equiripple FIR filters with inverse-Dirichlet-sinc-shaped passbands. The cutoff frequency in both designs is pi/4 radians/sample. Set C=1 in one design C=2 in the second design. The maximum passband and stopband ripple is 0.05. Set p=1 in one design and p=2 in the second design.
Design the filters.
b1 = firceqrip(30,0.25,[0.05 0.05],'invdiric',[1 1]); b2 = firceqrip(30,0.25,[0.05 0.05],'invdiric',[2 2]);
Obtain the filter frequency responses using freqz. Plot the magnitude responses.
[h1,~] = freqz(b1,1); [h2,w] = freqz(b2,1); plot(w,abs(h1)); hold on; plot(w,abs(h2),'r'); axis([0 pi 0 1.5]); xlabel('Radians/sample'); ylabel('Magnitude'); legend('C=1 p=1','C=2 p=2');

Inspect the stopband ripple in the design with C=1 and p=1. The constrained design sets the maximum ripple to be 0.05. Zoom in on the stopband from the cutoff frequency of pi/4 radians/sample to 3pi/4 radians/sample.
figure; plot(w,abs(h1)); set(gca,'xlim',[pi/4 3*pi/4]); grid on;

Extended Capabilities
Version History
Introduced in R2011a
See Also
diric | fdesign.decimator | firnyquist | firgr | ifir | iirgrpdelay | iirlpnorm | iirlpnormc | fircls | firls | firpm | sinc