Jet Pump (IL)

Liquid-liquid jet pump in an isothermal liquid network

• 

Libraries:
Simscape / Fluids / Isothermal Liquid / Pumps & Motors

Description

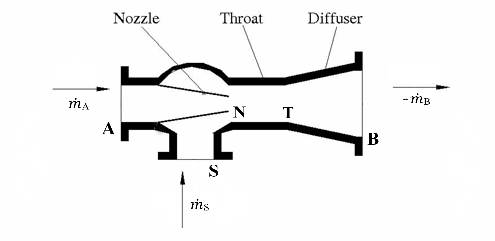
The Jet Pump (IL) block models a liquid-liquid jet pump in an isothermal liquid network. The motive and suction fluids in the jet pump are the same. The motive fluid enters the primary nozzle at port A and draws in the suction fluid through input port S. After mixing in the throat, the combined flow expands through the diffuser and discharges at port B. The total pressure change over the pump is the sum of the individual contributions of friction and area change in each section of the pump and momentum changes in the throat. The sign convention for the equations correspond to positive flow into the throat.

Changes in Pressure Due to Area Changes

The mass flow rate is conserved in the pump

$${\dot{m}}_A+{\dot{m}}_S+{\dot{m}}_B=0,$$

where $$\dot{m}$$_A is the mass flow rate through port A, $$\dot{m}$$_S is the mass flow rate through port S, and $$\dot{m}$$_A is the mass flow rate through port B.

Using mass conservation and the Bernoulli Principle, you can express the area changes over the pump segments in terms of pressure change. The pressure change associated with the nozzle is

$$\Delta p_{a,}{}_{Nozzle}=\frac{{\dot{m}}_A}{4\rho A_N^2},$$

or 0, whichever is greater. A_N is the value of the Nozzle exit area parameter and ρ is the fluid density.

The pressure change due to the area at the suction inlet is

$$\Delta p_{a,}{}_{Annulus}=\frac{{\dot{m}}_S}{4\rho {\left(A_T-A_N\right)}^2},$$

or 0, whichever is greater. A_T is the cross-sectional area of the throat. The pressure change over the diffuser expansion is

$$\Delta p_{a,}{}_{Diffuser}=-\frac{{\dot{m}}_B{}^2}{2\rho A_T^2}\left(1-a^2\right),$$

where a is the value of the Diffuser inlet to outlet area ratio parameter.

Reversed Flows

In the case of reversed flow, the block does not model the effect of the nozzle area on pressure change, and the flow traveling from the throat through the nozzle does not undergo any pressure gain. This behavior ensures the numerical stability of the block during simulation of reversed flows.

Changes in Pressure Due to Mixing

The motive and suction flows mix in the throat. The change in pressure from mixing is

$$\Delta p_{mixing}=\frac{\frac{{\dot{m}}_A^2}{b}+\frac{{\dot{m}}_S^2}{1-b}-{\dot{m}}_B^2}{\rho A_T},$$

where b is the value of the Nozzle exit to throat area ratio parameter, which is defined between the largest and smallest cross-sectional areas of the nozzle.

Pressure Losses Due to Friction

The flow loses pressure due to due to friction in the nozzle, secondary suction inlet, throat, and diffuser. The block calculates these losses based on a coefficient for each section and the area, or area ratio, between different sections of the pump. Friction causes pressure loss regardless of the flow direction. The pressure loss in the nozzle due to friction is

$$\Delta p_{f,Nozzle}=K_N\frac{{\dot{m}}_A\left|{\dot{m}}_A\right|}{2\rho A_N^2},$$

where K_N is the value of the Primary flow nozzle loss coefficient parameter. The pressure loss due to friction in the suction flow through the annulus is

$$\Delta p_{f,Annulus}=K_S\frac{{\dot{m}}_S\left|{\dot{m}}_S\right|}{2\rho {\left(A_T-A_N\right)}^2},$$

where K_S is the value of the Secondary flow entry loss coefficient parameter. The pressure loss in the throat due to friction is

$$\Delta p_{f,Throat}=K_T\frac{{\dot{m}}_B\left|{\dot{m}}_B\right|}{2\rho A_T^2},$$

where K_T is the value of the Throat loss coefficient parameter. The pressure loss in the diffuser due to friction is

$$\Delta p_{f,Diffuser}=K_D\frac{{\dot{m}}_B\left|{\dot{m}}_B\right|}{2\rho A_T^2},$$

where K_D is the value of the Diffuser loss coefficient parameter. The sign corresponds to negative flow from the throat toward port B. Because the block defines losses for the regions of highest velocity in the flow, the block uses the throat area, which is equal to the diffuser inlet area, in the diffuser loss equation.

Saturation Pressure in the Nozzle

Cavitation occurs when a region of low pressure in the flow falls below the vapor saturation pressure, which creates pockets of vapor in the liquid and impedes any further increase in flow through the pump. You can model this flow rate limit by specifying a minimum nozzle pressure. If the flow pressure is more than the value of the Minimum allowable nozzle pressure parameter, the fluid velocity remains constant. Between the nozzle and the diffuser, the pressure change is either

$$p_B-p_N=\Delta p_{mixing}+\Delta p_{f,Throat}+\Delta p_{f,Diffuser}-\Delta p_{a,Diffuser}$$

or $$p_B-p_{N,\min },$$ whichever is smaller.

The total pressure change in the nozzle is

$$p_A-p_N=\Delta p_{a,Nozzle}+\Delta p_{f,Nozzle}.$$

The total pressure change in the annulus is

$$p_S-p_N=\Delta p_{a,Annulus}+\Delta p_{f,Annulus}.$$

Assumptions and Limitations

• The motive and suction liquids are the same.

• Mixing in the throat is uniform and complete.

• The nozzle inlet is much larger than the nozzle outlet, and the suction jet annulus is much smaller than the suction inlet.

• For reversed flows, the block does not model change in pressure due to the nozzle.

• The block models any effect of cavitation as a maximum limit on the flow rate in the throat.

Examples

Well with Jet Pump

A well jet pump installation. The well jet pump installation presented in this example consists of a surface-mounted centrifugal pump and a jet pump installed in the well below the surface of the water.

• Open Model

Ports

Conserving

A — Liquid port

isothermal liquid

Isothermal liquid conserving port associated with the motive liquid inlet port.

S — Liquid port

isothermal liquid

Isothermal liquid conserving port associated with the suction liquid inlet port.

B — Liquid port

isothermal liquid

Isothermal liquid conserving port associated with the mixed fluid outlet port.

Parameters

Nozzle exit area — Nozzle exit area

1e-4 m^2 (default) | positive scalar

Cross-sectional area of the nozzle exit at its widest section.

Nozzle exit to throat area ratio — Nozzle outlet to throat area

0.25 (default) | positive scalar

Characteristic ratio of the nozzle outlet and throat cross-sectional areas.

Diffuser inlet to outlet area ratio — Diffuser geometry ratio

0.25 (default) | positive scalar

Characteristic ratio of the diffuser inlet and outlet cross-sectional areas.

Primary flow nozzle loss coefficient — Primary flow friction loss coefficient

0.05 (default) | positive scalar

Loss coefficient that characterizes the losses in pressure due to nozzle friction in the motive flow.

Secondary flow entry loss coefficient — Secondary flow friction loss coefficient

0.005 (default) | positive scalar

Loss coefficient that characterizes the losses in pressure in the suction flow due to the suction inlet friction.

Throat loss coefficient — Throat friction loss coefficient

0.1 (default) | positive scalar

Loss coefficient that characterizes the losses in pressure in the mixture due to throat friction.

Diffuser loss coefficient — Diffuser friction loss coefficient

0.1 (default) | positive scalar

Loss coefficient that characterizes the losses in pressure due in the mixed flow due to friction in the diffuser.

Minimum allowable nozzle pressure — Minimum pressure at nozzle outlet

1 Pa (default) | positive scalar

Minimum allowed pressure in the jet pump. If the pressures at the nozzle exit fall below this value, the block simulates the effects of cavitation by restricting the fluid velocity to the velocity at the minimum nozzle pressure.

Extended Capabilities

C/C++ Code Generation
Generate C and C++ code using Simulink® Coder™.

Version History

Introduced in R2020a