Control Format Indicator (CFI) Channel
When transmitting data on the downlink in an OFDM communication system, it is important to specify how many OFDM symbols are used to transmit the control channels so the receiver knows where to find control information. In LTE, the Control Format Indicator (CFI) value defines the time span, in OFDM symbols, of the Physical Downlink Control Channel (PDCCH) transmission (the control region) for a particular downlink subframe. The CFI is transmitted using the Physical Control Format Indicator Channel (PCFICH).
Control Format Indicator Values
The CFI is limited to the value 1, 2, or 3. For bandwidths greater than ten resource blocks, the number of OFDM symbols used to contain the downlink control information is the same as the actual CFI value. Otherwise, the span of the downlink control information (DCI) is equal to CFI+1 symbols.
PCFICH Resourcing
The PCFICH is mapped in terms of Resource Element Groups (REGs) and is always mapped onto the first OFDM symbol. The number of REGs allocated to the PCFICH transmission is fixed to 4 i.e. 16 Resource Elements (REs). A PCFICH is only transmitted when the number of OFDM symbols for PDCCH is greater than zero.
CFI Channel Coding
The CFI value undergoes channel coding to form the PCFICH payload, as shown in the following figure.

Using the following table contains the CFI codeword for each CFI value. Using these codewords corresponds to a block encoding rate of 1/16, changing a two bit CFI value to a 32 bit codeword.
| CFI | CFI codeword <b0, b1, ... , b31> |
|---|---|
| 1 | <0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1> |
| 2 | <1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0> |
| 3 | <1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1,0,1,1> |
| 4 (Reserved) | <0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0> |
The PCFICH
The coded CFI is scrambled before undergoing QPSK modulation, layer mapping and precoding as shown in the following figure.

Scrambling
The 32-bit coded CFI block undergoes a bit-wise exclusive-or (XOR) operation with a cell-specific scrambling sequence. The scrambling sequence is a pseudo-random sequence created using a length-31 Gold sequence generator. At the start of each subframe, it is initialized using the slot number within the radio frame, , and the cell ID, .
Scrambling with a cell specific sequence serves the purpose of intercell interference rejection. When a UE descrambles a received bit stream with a known cell specific scrambling sequence, interference from other cells will be descrambled incorrectly and will only appear as uncorrelated noise.
Modulation
The scrambled bits are then QPSK modulated to create a block of complex-valued modulation symbols.
Layer Mapping
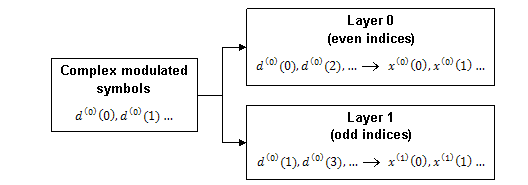
The complex symbols are mapped to one, two, or four layers depending on the number of transmit antennas used. The complex modulated input symbols, , are mapped onto v layers, .
If a single antenna port is used, only one layer is used. Therefore, .
If transmitter diversity is used, the input symbols are mapped to layers based on the number of layers.
Two Layers — Even symbols are mapped to layer 0 and odd symbols are mapped to layer 1, as shown in this figure.
Four Layers — The input symbols are mapped to layers sequentially, as shown in the following figure.

Precoding
The precoder takes a block from the layer mapper, , and generates a sequence for each antenna port, . The variable p is the transmit antenna port number, and can assume values of {0}, {0,1}, or {0,1,2,3}.
For transmission over a single antenna port, no processing is carried out, as shown in this equation.
Precoding for transmit diversity is available on two or four antenna ports.
Two Antenna Port Precoding. An Alamouti scheme is used for precoding, which defines the relationship between input and output as shown in the following equation.
In the Alamouti scheme, two consecutive symbols, and , are transmitted in parallel using two antennas with the following mapping, where the asterisk symbol (*) denotes the complex conjugate operation.
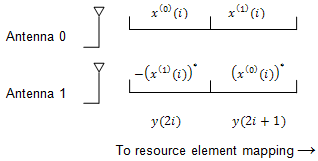
Since any two columns in the precoding matrix are orthogonal, the two symbols, and , can be separated at the UE.
Four Antenna Port Precoding. Precoding for the four antenna port case defines the relationship between the input and output as shown in the following equation.
In this scheme, two consecutive symbols are transmitted in parallel in two symbol periods using four antennas with this mapping, where the asterisk symbol (*) denotes the complex conjugate operation.

Mapping to Resource Elements
The complex valued symbols for each antenna are divided into quadruplets for mapping to resource elements. Each quadruplet is mapped to a Resource element Group (REG) within the first OFDM symbol. There are sixteen complex symbols to be mapped therefore four quadruplets are created.
The first quadruplet is mapped onto a REG with subcarrier index , given by the following equation.
The subsequent three quadruplets are mapped to REGs spaced at intervals of from the first quadruplet and each other. This spreads the quadruplets, and hence the PCFICH, over the entire subframe as illustrated in the following figure.

See Also
lteCFI | ltePCFICH | ltePCFICHInfo | ltePCFICHIndices | lteDLResourceGrid | lteSymbolModulate | lteSymbolDemodulate | ltePCFICHPRBS | lteLayerMap | lteLayerDemap | lteDLPrecode | lteDLDeprecode