Constraints on Linear Combinations of Inputs and Outputs
You can constrain linear combinations of plant input and output variables. For example, you can constrain a particular manipulated variable (MV) to be greater than a linear combination of two other MVs.
The general form of such constraints is:

Here:
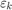 is the QP slack variable used for constraint softening. For more information, see Constraint Softening.
is the QP slack variable used for constraint softening. For more information, see Constraint Softening. are the
are the 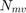 manipulated variable values, in engineering units.
manipulated variable values, in engineering units.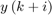 are the
are the  predicted plant outputs, in engineering units.
predicted plant outputs, in engineering units.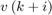 are the
are the  measured plant disturbance inputs, in engineering units.
measured plant disturbance inputs, in engineering units. ,
,  ,
,  ,
,  , and
, and  are constant matrices and vectors. For more information, see
are constant matrices and vectors. For more information, see setconstraint.
As with the QP cost function, output prediction using the state observer makes these constraints a function of the QP decision variables.
To set the mixed input/output constraints of an MPC controller, use the setconstraint function. To obtain the existing constraints from a controller, use getconstraint.
When using mixed input/output constraints, consider the following:
Mixed input/output constraints are dimensional by default.
Run-time updating of mixed input/output constraints is supported at the command line and in Simulink®. For more information, see Update Constraints at Run Time.
Using mixed input/output constraints is not supported in MPC Designer.
As an example, consider an MPC controller for a double-integrator plant with mixed input/output constraints.
Create Initial MPC Controller
The basic setup of the MPC controller includes:
A double integrator as the prediction model
Prediction horizon of 20
Control horizon of 20
Input constraints:
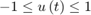
plant = tf(1,[1 0 0]); Ts = 0.1; p = 20; m = 20; mpcobj = mpc(plant,Ts,p,m); mpcobj.MV = struct('Min',-1,'Max',1);
-->"Weights.ManipulatedVariables" is empty. Assuming default 0.00000. -->"Weights.ManipulatedVariablesRate" is empty. Assuming default 0.10000. -->"Weights.OutputVariables" is empty. Assuming default 1.00000.
Define Mixed Input/Output Constraints
Constrain the sum of the input u(t) and output y(t) must be nonnegative and smaller than 1.2:

To impose this combined (mixed) I/O constraint, formulate it as a set of inequality constraints involving  and
and  .
.

To define these constraints using the setconstraint function, set the constraint constants as follows:
![$$E = \left[ {\begin{array}{*{20}{c}} 1\\ { - 1} \end{array}} \right],\;F = \left[ {\begin{array}{*{20}{c}} 1\\ { - 1} \end{array}} \right],\;G = \left[ {\begin{array}{*{20}{c}} {1.2}\\ 0 \end{array}} \right]$$](../../examples/mpc/win64/mpcmixedconstraints_eq14304708454108056021.png)
setconstraint(mpcobj,[1;-1],[1;-1],[1.2;0]);
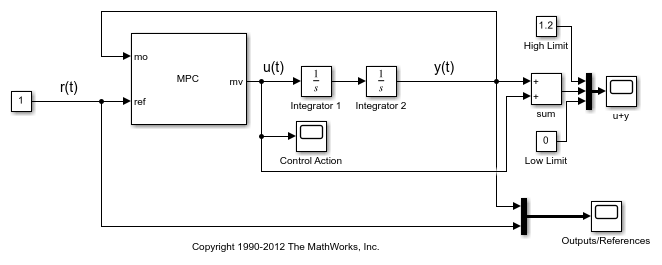
Simulate Controller
Simulate closed-loop control of the linear plant model in Simulink. The controller mpcobj is specified in the MPC Controller block.
mdl = 'mpc_mixedconstraints';
open_system(mdl)
sim(mdl)
-->Converting the "Model.Plant" property to state-space. -->Converting model to discrete time. Assuming no disturbance added to measured output #1. -->"Model.Noise" is empty. Assuming white noise on each measured output.
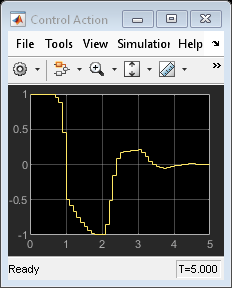
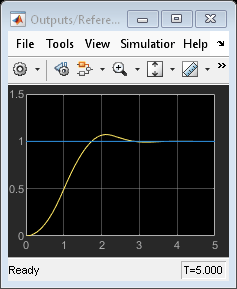
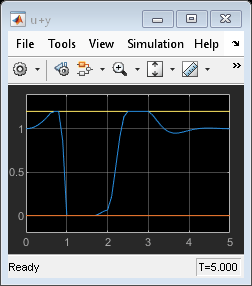
The MPC controller keeps the sum  between 0 and 1.2 while tracking the reference signal,
between 0 and 1.2 while tracking the reference signal, 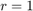 .
.
bdclose(mdl)