Eigenvalues and Eigenmodes of L-Shaped Membrane: PDE Modeler App
This example shows how to compute all eigenmodes with eigenvalues smaller than 100 for the eigenmode PDE problem
–Δu = λu
on the geometry of the L-shaped membrane. The boundary condition is the Dirichlet condition u = 0. This example uses the PDE Modeler app. For a programmatic workflow, see Eigenvalues and Eigenmodes of L-Shaped Membrane.
To solve this problem in the PDE Modeler app, follow these steps:
Draw a polygon with the corners (0,0), (–1,0), (–1,–1), (1,–1), (1,1), and (0,1) by using the
pdepolyfunction.pdepoly([0,-1,-1,1,1,0],[0,0,-1,-1,1,1])
Check that the application mode is set to Generic Scalar by selecting Options > Application.
Use the default Dirichlet boundary condition u = 0 for all boundaries. To verify it, switch to boundary mode by selecting Boundary > Boundary Mode. Use Edit > Select all to select all boundaries. Select Boundary > Specify Boundary Conditions and verify that the boundary condition is the Dirichlet condition with
h = 1,r = 0.Specify the coefficients by selecting PDE > PDE Specification or clicking the
 button on the toolbar. This is an eigenvalue
problem, so select the Eigenmodes type of PDE. The general
eigenvalue PDE is described by . Thus, for this problem, use the default coefficients
button on the toolbar. This is an eigenvalue
problem, so select the Eigenmodes type of PDE. The general
eigenvalue PDE is described by . Thus, for this problem, use the default coefficients c = 1,a = 0, andd = 1.Specify the maximum edge size for the mesh by selecting Mesh > Parameters. Set the maximum edge size value to 0.05.
Initialize the mesh by selecting Mesh > Initialize Mesh.
Specify the eigenvalue range by selecting Solve > Parameters. In the resulting dialog box, use the default eigenvalue range
[0 100].Solve the PDE by selecting Solve > Solve PDE or clicking the
 button on the toolbar. By default, the app plots
the first eigenfunction.
button on the toolbar. By default, the app plots
the first eigenfunction.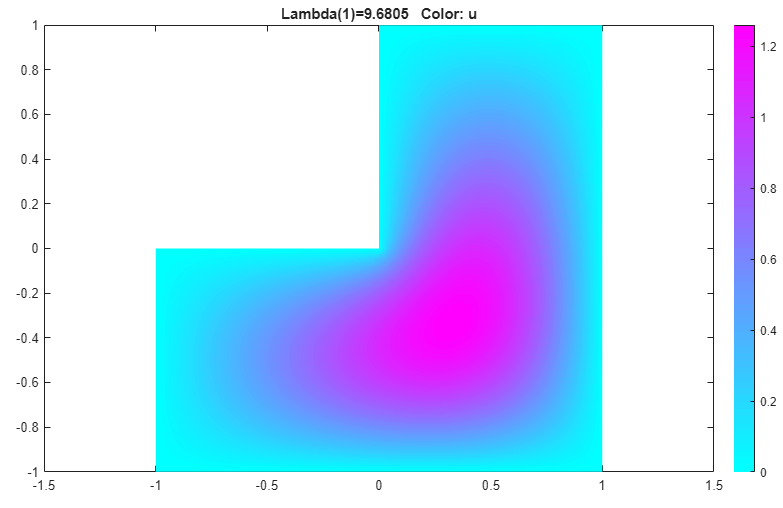
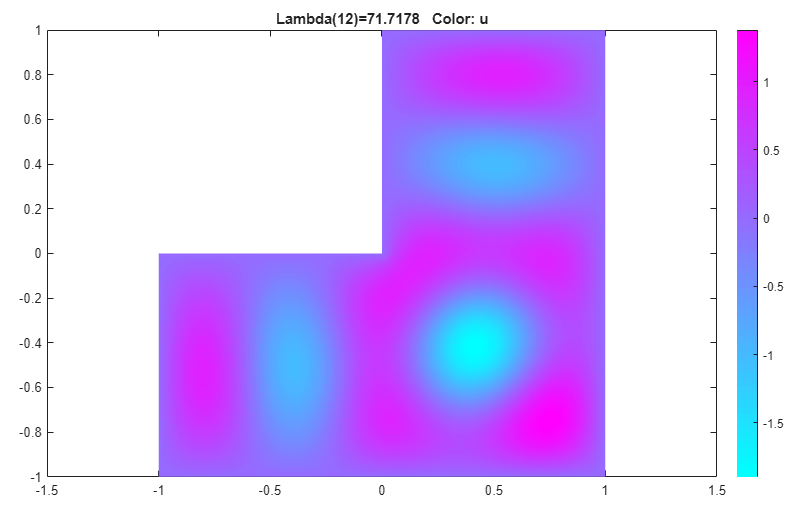
Plot other eigenfunctions by selecting Plot > Parameters and then selecting the corresponding eigenvalue from the drop-down list at the bottom of the dialog box. For example, plot the 12th eigenfunction in the specified range.