Minimal Surface Problem: PDE Modeler App

This example shows how to solve the minimal surface equation

$$-\nabla \cdot \left(\frac{1}{\sqrt{1+{\left|\nabla u\right|}^2}}\nabla u\right)=0$$

on the unit disk Ω = {(x,y) | x² + y² ≤ 1}, with u = x² on the boundary ∂Ω.

This example uses the PDE Modeler app. For the programmatic workflow, see Minimal Surface Problem.

An elliptic equation in the toolbox form is

$$-\nabla \cdot \left(c\nabla u\right)+au=f$$

Therefore, for the minimal surface problem the coefficients are as follows:

$$c=\frac{1}{\sqrt{1+{\left|\nabla u\right|}^2}},a=0,f=0$$

Because the coefficient c is a function of the solution u, the minimal surface problem is a nonlinear elliptic problem.

To solve the minimal surface problem in the PDE Modeler app, follow these steps:

1. Model the surface as a unit circle.

   pdecirc(0,0,1)

2. Check that the application mode is set to Generic Scalar.

3. Specify the boundary conditions. To do this:

   1. Switch to boundary mode by clicking the button or selecting Boundary > Boundary Mode.

   2. Select all boundaries by selecting Edit > Select All.

   3. Select Boundary > Specify Boundary Conditions.

   4. Specify the Dirichlet boundary condition u = x². To do this, specify h = 1, r = x.^2.

4. Specify the coefficients by selecting PDE > PDE Specification or clicking the button on the toolbar. Specify c = 1./sqrt(1+ux.^2+uy.^2), a = 0, and f = 0.

5. Initialize the mesh by selecting Mesh > Initialize Mesh.

6. Refine the mesh by selecting Mesh > Refine Mesh.

7. Choose the nonlinear solver. To do this, select Solve > Parameters and check Use nonlinear solver. Set the tolerance parameter to 0.001.

8. Solve the PDE by selecting Solve > Solve PDE or clicking the button on the toolbar.

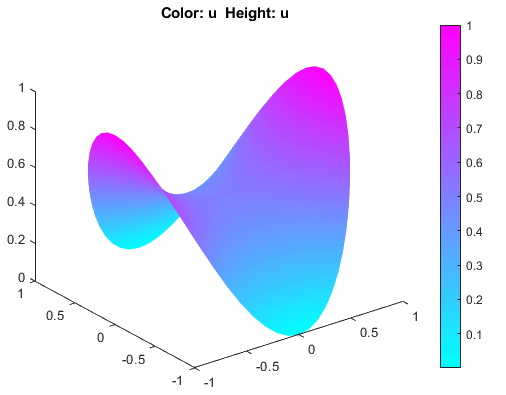
9. Plot the solution in 3-D. To do this, select PlotParameters. In the resulting dialog box, select Height (3-D plot).