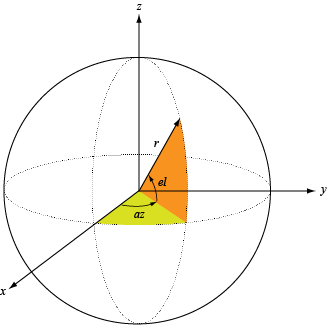
patternElevation
Syntax
Description
patternElevation(
plots the array pattern with additional options specified by one or more
array,FREQ,AZ,Name,Value)Name,Value pair arguments.
Input Arguments
Name-Value Arguments
Output Arguments
More About
Version History
Introduced in R2021a