phased.Receiver
Description
The phased.Receiver
System object™ models a multichannel receiver. The object supports system-level multi-channel
receiver chains that include impairments such as nonlinear gain, system noise, and phase
offsets.
To create a receiver
Create the
phased.Receiverobject and set its properties.Call the object with arguments, as if it were a function.
To learn more about how System objects work, see What Are System Objects?
Creation
Description
recvr = phased.Receiverrecvr.
recvr = phased.Receiver(Name=Value)recvr with each specified property Name set to
the specified Value. You can specify additional name-value pair
arguments in any order as (Name1=Value1, …
,NameN=ValueN).
Properties
The order that receiver effects are applied to the signal is fixed. The following list describes the order in which effects are applied to the input signal. All properties need not be included but if they are, they will be applied in this order regardless of the order in which their properties are listed::
System noise is added according to the method specified in
NoiseMethodproperty.The signal gain is applied according to the method specified in
GainMethodproperty. This gain may be linear or non-linear as a function of input power.A phase offset is added to the signal according to the
PhaseOffsetproperty.
Properties can be applied to N channels by specifying properties as an N-element vector. If a property is specified as a scalar, it will be expanded to match the size of vector properties. Scalars are expanded to length-N vectors containing the scalar value.
Unless otherwise indicated, properties are nontunable, which means you cannot change their
values after calling the object. Objects lock when you call them, and the
release function unlocks them.
If a property is tunable, you can change its value at any time.
For more information on changing property values, see System Design in MATLAB Using System Objects.
Receiver configuration, specified as "Budget" or
"Cascade". This property defines how effects are applied to the receiver.
If the
Configurationproperty is set to"Budget", the following list describes the order in which effects are applied to the input signal.If
EnableInputPortSetistrue, set the input signal to zero for any disabled points.Add input noise to the signal according to the
AddInputNoiseproperty setting.Add system noise according to the method specified in the
NoiseMethod property.Add signal gain according to the method specified in
GainMethodproperty.Add a phase offset to the signal according to the
PhaseOffsetproperty.
If the
Configurationis"Cascade", the input signal is first disabled according toEnableInputPortsproperty and then propagated through each component in theCascadeproperty to generate the output.
Example: Configuration="Cascade"
Data Types: char | string
Cascade components, specified as a 1-by-N cell array. Place compatible objects in series to define the behavior of the transmitter. Below is a list of compatible components. An empty cell array has no effect on the signal.
Compatible components
rf.Amplifier(RF Toolbox)rf.Mixer(RF Toolbox)rf.PAmemory(RF Toolbox)rf.Sparameter(RF Toolbox)rf.Filter(RF Toolbox)
Dependencies
To enable this property, set the Configuration property to
"Cascade".
Data Types: cell
Set this property to true to allow the receiver to accept the
input enabling signal, EN. If you do not want to specify a receiver
enabling signal set this property to false.
Example: EnableInputPort=true
Data Types: logical
Set this property to true to add noise to the input signal prior
to applying receiver effects. The InputNoiseTemperature property
and the SampleRate property together determine the noise power. The
SampleRate property determines the noise bandwidth.
Example:
true
Dependencies
To enable this property set the Configuration property to
"Budget".
Data Types: logical
Input noise temperature, specified as a positive scalar or
length-N vector of positive values where N is
the number of receiver channels. If InputNoiseTemperature is a
scalar, the same value is applied to all channels. Units are in Kelvin degrees.
Example: 300
Dependencies
To enable this property, set the AddInputNoise property to
true.
Data Types: single | double
Method for defining the system noise, specified as 'None', 'Noise figure', 'Noise factor' or 'Noise temperature'.
When set to
'None', no noise is applied.When set to
'Noise figure', theNoiseFigureproperty determines the noise level.When set to
'Noise temperature', theNoiseTemperatureproperty determines the noise level.When set to
'Noise factor', theNoiseFactorproperty determines the noise level.
The noise bandwidth is derived from the input signal sample rate.
Example: 'Noise figure'
Dependencies
To enable this property, set the Configuration property to
"Budget".
Data Types: char | string
Receiver noise figure, specified as a real scalar or length-N
vector of real values. N is the number of channels. If
NoiseFigure is a scalar, the same value is applied to all
channels. Noise is generated with respect to the temperature defined by the
ReferenceTemperature property.
Dependencies
To enable this property, set the Configuration property to
"Budget" and the NoiseMethod property to
'Noise figure'.
Data Types: single | double
Receiver noise factor, specified as a positive scalar or length-N
vector of positive values. N is the number of channels. If
NoiseFactor is a scalar, the same value is applied to all
channels. Noise is generated with respect to the temperature defined by the
ReferenceTemperature property.
Dependencies
To enable this property, set the Configuration property to
"Budget" and the NoiseMethod property to
'Noise factor'.
Data Types: single | double
Equivalent noise temperature, specified as a positive scalar or length-N vector of positive values. N is the number of channels. If NoiseTemperature is a scalar, the same value is applied to all channels. Units are in K.
Dependencies
To enable this property, set the NoiseMethod to 'Noise temperature'.
Data Types: single | double
Reference temperature, specified as a positive scalar or a length-N vector of positive values. N is the number of channels. If ReferenceTemperature is a scalar, the same value is applied to all channels.
Dependencies
To enable this property, set the NoiseMethod property to 'Noise figure' or 'Noise factor'.
Data Types: single | double
Sample rate of the input signal, specified as a positive scalar. Use this property to add noise to the signal. The SampleRate is only used to derive the noise bandwidth of the signal.
Dependencies
To enable this property, set the AddInputNoise property to true or set the NoiseMethod property to 'Noise figure', 'Noise factor', or 'Noise temperature'.
Data Types: single | double
Method for applying gain to the received signal, specified as
'Linear', 'Cubic polynomial' or 'Lookup
table'.
When set to
'Linear', linear gain is applied.When set to
'Cubic polynomial', a cubic polynomial model is used to apply non-linear gain.When set to
'Lookup Table', a lookup table is defined to directly specify output power and phase shift as a function of input power.
Dependencies
To enable this property, set the Configuration property to
Budget.
Data Types: char | string
Linear receiver gain, specified as a real scalar or length-N
vector of real values. N is the number of channels. If
Gain is a scalar, the same value is applied to all channels.
Units are in dB.
Dependencies
To enable this property, set the GainMethod property to
'Linear' or 'Cubic polynomial'.
Data Types: single | double
Output third-order intercept point (OIP3). specified as a scalar or length-N vector of real values. N is the number of channels. OIP3 expresses the non-linearity of the transmitter or receiver. If OIP3 is a scalar, the same value is applied to all channels. See Nonlinearities and Noise in Idealized Baseband Amplifier Block (RF Blockset) for a detailed discussion of OIP3. Units are in dBm.
Dependencies
To enable this property, set the GainMethod property to 'Cubic polynomial'.
Data Types: single | double
AM/AM-AM/PM lookup table, specified as a 3-by-M-by-N real-valued array. The lookup table specifies amplifier power characteristics. M is the number of table entries and N is the number of channels. Each row in the table expresses the relationship between output power or phase change as a function of input power. Specify AM/AM (in dB/dB) and AM/PM (in deg/dB) characteristics in a [Pin(dBm),Pout(dBm),Phase shift(degrees)]-by-M matrix or [Pin(dBm),Pout(dBm),Phase shift(degrees)]-by-M-by-N array. Use the table to linear interpolate or extrapolate power values. The column 1 input power must increase monotonically. There must be at least 3 rows in the table. The power output can be written as:
Dependencies
To enable this property, set the GainMethod property to
'Lookup table'.
Data Types: single | double
Phase offset, specified as a real scalar or length-N vector of real values. N is the number of channels. If PhaseOffset is a scalar, the same value is applied to all channels. Units are in degrees.
Dependencies
To enable this property, set the Configuration property to
'Budget'.
Data Types: single | double
'Auto' | The default MATLAB® random number generator produces the
random numbers. Use 'Auto' if you are using this
object with Parallel Computing Toolbox™ software. |
'Property' | The object uses its own private random number generator to
produce random numbers. The Seed property of
this object specifies the seed of the random number generator. Use 'Property' if
you want repeatable results and are not using this object with Parallel Computing Toolbox software. |
Dependencies
Randomization occurs if:
you set the
CoherentOnTransmitproperty tofalseand theNoiseMethodis not set to'None',or set the
Configurationproperty to"Cascade"and randomization is performed by an object listed in theCascadeproperty.
To use this object with the Parallel Computing Toolbox, set this property to 'Auto'.
Data Types: char | string
Random number generator seed, specified as a nonnegative integer between 0 and 232–1.
Dependencies
To enable this property, set the SeedSource property to
'Property'.
Data Types: double | single
Usage
Description
Input Arguments
Receiver Input signal voltage, specified as a complex-valued vector or complex-valued matrix. The number of rows is equal to the number of samples.
If X is a vector, the number of rows in
Y equals the number of rows in X.The
number of columns in Y equals the number of channels in the
receiver.
In the case where X is a vector, the number of channels is
determined by the active properties that indicate a number of channels, such as
NoiseFigure, ReferenceTemperature,
Gain, or PhaseOffset.
Receiver effects are applied to the signal in a fixed order although some effects can be omitted. The order in which effects are applied to the input signal:
Set input signal to
falsefor any disabled points if theEnableInputPortproperty istrue.Input noise is added according to the
AddInputNoiseproperty.System noise is added according to the method specified in
NoiseMethodproperty.Signal gain is applied according to the method specified in the
GainMethodproperty.Phase offset is added to the signal according to
PhaseOffsetproperty.
Data Types: single | double
Complex Number Support: Yes
Enabling signal, specified as a real-valued vector or matrix or logical-valued vector or matrix.
If
ENis a vector, it must have the same number of rows as the input signal matrixX. Then, the value in each row ofENis applied to all the columns ofX.If
ENis a matrix,ENmust be the same size asX, and each element inENis applied to the corresponding element inX.
If EN is of type single or double, when an element of
EN is zero,the receiver is turned off, and the input signal is
set to zero. When element of EN is nonzero, the receiver is
turned on, and the input passes through the receiver.
If EN is logical, the receiver is enabled whenever an element
of EN is true and disabled whenever an element
of EN is false.
Dependencies
To enable this argument, set the EnableInputPort property
to true.
Data Types: double | single | logical
Output Arguments
Receiver output signal voltage, returned as a complex-valued vector or
complex-valued matrix. If X is a matrix, the size of
Y is equal to the size of X. The
transformation is based on transmitter characteristics, such as the gain,
nonlinearity, and noise. Power is calculated from signal voltage assuming a reference
impedance of 1 Ohm.
Data Types: single | double
Complex Number Support: Yes
Object Functions
To use an object function, specify the
System object as the first input argument. For
example, to release system resources of a System object named obj, use
this syntax:
release(obj)
viewGain | Plot output receiver power or output phase shift as a function of input receiver power |
viewLayout | Draws the layout of the receiver |
Examples
Display a waveform that is output from a single-channel receiver having linear gain. Specify noise setting the NoiseMethod property to 'Noise figure'.
fs = 1e7;
waveform = phased.LinearFMWaveform(SampleRate=fs, ...
PulseWidth=1e-5,SweepBandwidth=5e6);
sig = waveform();Create a receiver object. Apply a 20 dB gain and then add noise to the waveform.
recvr = phased.Receiver(AddInputNoise=true,InputNoiseTemperature=200, ... GainMethod="Linear",Gain=20,NoiseMethod="Noise figure", ... NoiseFigure=5,SampleRate=1e6,PhaseOffset=0);
Pass the waveform through the receiver to create the processed waveform.
y = recvr(sig);
Plot the absolute value of the original waveform and the amplified waveform as a function of time.
dt = 1/fs; n = length(sig); t = (0:(n-1))*dt*1e6; plot(t,abs(sig)) hold on plot(t,abs(y)) hold off legend('Original waveform','Amplified waveform') xlabel('Time (microsec)') ylabel('Signal')

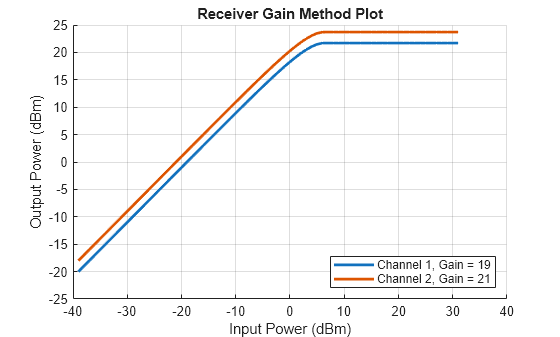
Receive a linear FM waveform with a two-channel receiver where the behavior varies between each channel. Use a cubic polynomial gain model to simulate non-linear gain behavior and specify noise using noise temperature. The receiver sample rate is 10 Mhz.
fs = 10e6;
waveform = phased.LinearFMWaveform(SampleRate=fs, ...
PulseWidth=1e-5,SweepBandwidth=5e6);
x = waveform();Create the two channel receiver.
recvr = phased.Receiver(GainMethod="Cubic polynomial",Gain=[19,21], ... OIP3=[30,32],NoiseMethod="Noise temperature", ... NoiseTemperature=[290,350],SampleRate=fs,PhaseOffset=[0,15]);
Pass the waveform through the receiver.
y = recvr(x); viewGain(recvr,ChannelIndex=1,Parent=gca); hold on viewGain(recvr,ChannelIndex=2,Parent=gca); legend('Channel 1, Gain = 19','Channel 2, Gain = 21', ... 'Location','SouthEast') hold off
More About
You can use the phased.Receiver
System object in place of the phased.ReceiverPreamp in many case. Here
are some guidelines for replacing phased.ReceiverPreamp properties by equivalent phased.Receiver properties.
You can replace the
Gainproperty of thephased.ReceiverPreampSystem object with theGainproperty of thephased.Receiverbut first you must specify that the gain is linear. To do this, set theGainMethodproperty of thephased.Receiverto"Linear".There is no property in
phased.Receiverequivalent to theLossproperty of thephased.ReceiverPreamp. Loss can be obtained by offsetting theGain.Both the
phased.ReceiverPreampand thephased.ReceiverSystem objects lets you add noise to the receiver output. You can obtain equal noise powers by proper choice of the properties of each objectFor the
phased.ReceiverPreamp, you can specify the noise using theNoiseMethodproperty set to either"Noise power"or"Noise temperature".Setting the
NoiseMethodproperty to"Noise temperature"adds complex baseband noise to the input signal. The quantityrepresents the noise power computed from the (TRef), the
NoiseFactor(F), and theSampleRate(fs) properties. The noise bandwidth (BW) is one-half the sample rate.Setting the
NoiseMethodproperty to"Noise power"lets you specify the noise power (NP) directly using theNoisePowerproperty.
The
phased.ReceiverSystem object does not have a"Noise power"option available in itsNoiseMethodproperty. The only options are"Noise figure","Noise factor","None", and"Noise temperature".When the
NoiseMethodproperty is set to"Noise temperature", use theNoiseTemperatureproperty to derive the noise power. The noise power (NP) iswhere k is Boltzmann's constant, TN is the noise temperature given by the
NoiseTemperatureproperty, and the bandwidth (BW) is one-half the sample rate.When the
NoiseMethodproperty is set to"Noise figure"or"Noise factor", the noise power can be derived using either quantity. First compute the noise factorwhere TN is the noise temperature set by the
NoiseTemperatureproperty and TRef is the reference temperature set by theReferenceTemperatureproperty. Compute the noise temperaturefrom the noise factor (F). Using this expression for the noise temperature, obtain the noise power
completely in terms of the noise factor.
Instead of the noise factor you can use the noise figure (in dB) FdB. The noise figure is related to the noise factor (F) by
and can be used when the
NoiseMethodproperty is set to"Noise figure".
Because of how the
phased.ReceiverPreampadds noise to the signal, the System object does not apply noise correctly. Thephased.ReceiverPreampSystem object adds noise to the signal after applying the gain. In contrast, thephased.ReceiverSystem object adds noise to the signal before applying the gain.Referring back to the general form of the noise factor,
set the noise factor of the
phased.Receiverso that its output noise power equals the output noise factor of thephased.ReceiverPreamp.To obtain the same output noise power, you must adjust the noise factor F (or equivalently the noise figure).
Algorithms
Cubic polynomials can be used to model nonlinear amplifier power gain. The general form of the cubic nonlinear AM-AM amplifier is characterized by
where u is the input power and
FAM-AM(u) is the output
power. c1 represents the linear gain in the
Gain property.
and OIP3 is the third-order intercept point specified by the
OIP3 property.
A lookup table expresses the relationship between output power or phase change as a function of input power at discrete points. The table contains values for TAM-AM and TAM-PM. The output power is derived by linear interpolation or extrapolation of
between these values.
Active properties by configuration
| Properties | Description | Budget active | Cascade active |
| Configuration | Receiver configuration | Y | Y |
| Cascade | Cascaded components | N | Y |
| AddInputNoise | Add noise to input signal | Y | |
| NoiseMethod | Noise method | Y | |
| NoiseFigure | Noise figure | Y | |
| NoiseFactor | Noise factor | Y | |
| NoiseTemperature | Input noise temperature | Y | |
| ReferenceTemperature | Reference temperature | Y | |
| SampleRate | Sample rate | Y | |
| GainMethod | Gain method | Y | |
| Gain | Receiver gain | Y | |
| OIP3 | Output OIP | Y | |
| Table | AM/AM-AM/FM lookup table | Y | |
| PhaseOffset | Phase offset | Y | |
| EnableInputPort | Enable receiver input port | Y | Y |
| Source of seed for random number generator | Seed source | Y | |
| Seed for random number generator | Seed | Y |
References
[1] Mark Richards, Fundamentals of Radar Signal Processing, McGraw-Hill, 2005.
[2] Merrill Skolnik, Introduction to Radar Systems, 3rd Ed., McGraw-Hill, 2001.
[3] Byron Edde, Radar: Principles, Technology, Applications, Prentice Hall, 1993.
[4] Behzad Razavi, RF Microelectronics, Second Edition, Wiley, 2012.
Extended Capabilities
Usage notes and limitations:
See System Objects in MATLAB Code Generation (MATLAB Coder).
Version History
Introduced in R2024aThe receiver now supports two separate configurations to be applied to different
operating modes: Budget and Cascade.
The System object lets you create multichannel data that incorporates impairments such as gain nonlinearities, signal noise, phase offsets, and random phase shifts.
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)