Operating Point for Van der Pol Oscillator
This example shows advantage of initialization with a Simscape operating point (OP) for a Van der Pol oscillator. OP initialization enables pushing the Van der Pol oscillator directly into its periodic steady state.
Model
A Van der Pol oscillator is a self-maintained electrical circuit made up of an inductor, a capacitor, and a nonlinear resistor. Van der Pol oscillator evolves in time according to the second-order differential equation:
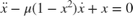
where  is the normalized current, and
is the normalized current, and 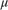 is a scalar parameter indicating the strength of nonlinear damping.
is a scalar parameter indicating the strength of nonlinear damping.
When 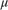 >0, the system dynamic result in a periodic motion called limit cycle. Near the origin
>0, the system dynamic result in a periodic motion called limit cycle. Near the origin 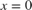 , the system is unstable, and far from the origin, the system is damped.
, the system is unstable, and far from the origin, the system is damped.

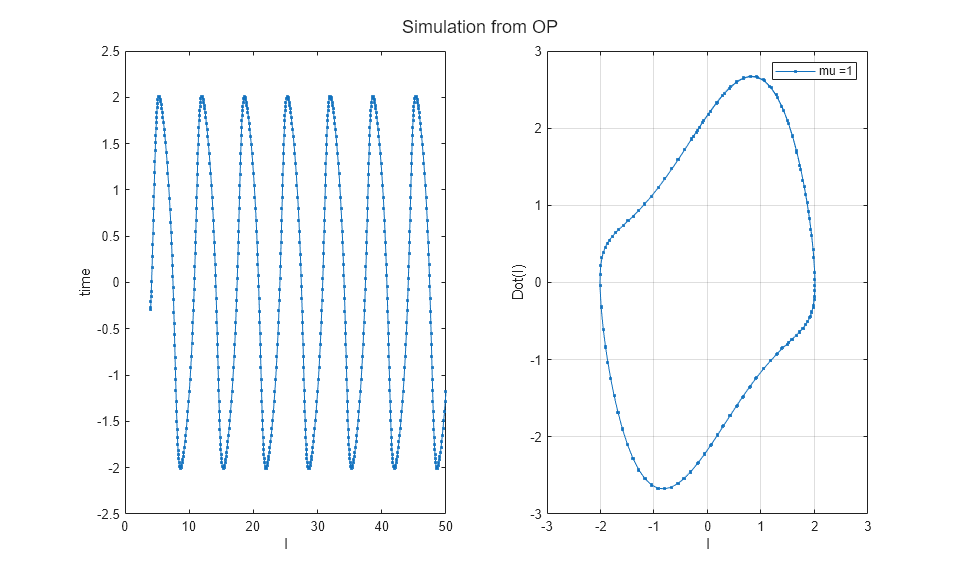
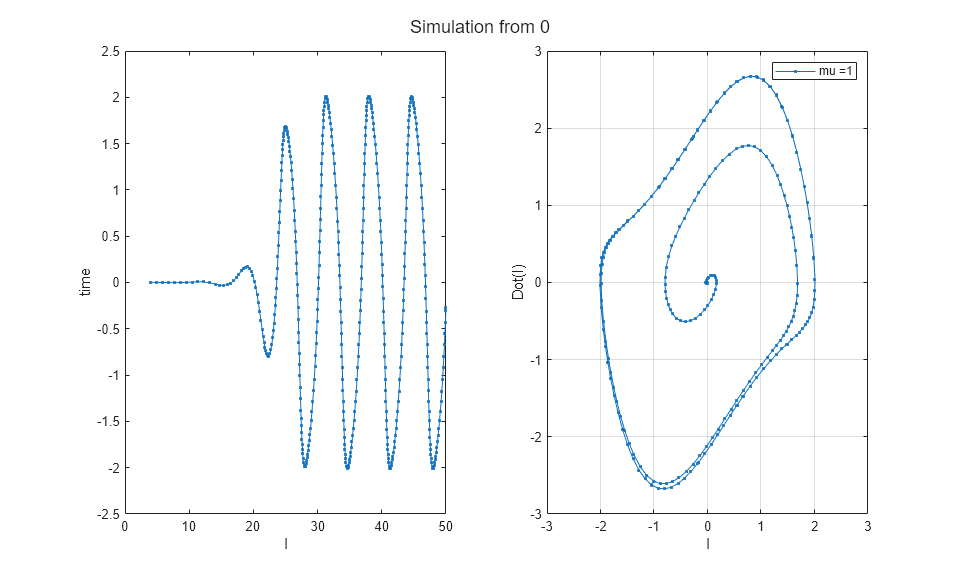
Limit Cycle Behavior Without An Operating Point
The simulation runs long enough for the oscillator to reach a periodic steady state. The left figure illustrates the dynamic behavior of current which converges to the steady state at some point. Another way to visualize the state dynamics is to plot a phase portrait of 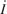 vs
vs 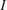 (see plot on the right). Observe that Van der Pol oscillator converges to a limit cycle.
(see plot on the right). Observe that Van der Pol oscillator converges to a limit cycle.
Create Simscape Operating Point
Extract a steady-state Simscape operating point for the model by using simscape.op.create and the Simscape log result from the previous simulation. Use '30' as the time because the simulation had visually reached the steady state by that time.
Limit Cycle Behavior With An Operating Point
Validate the operating point by initializing the Van der Pol oscillator model with the operating point. The resulting behavior is the steady-state limit cycle without the transient spiral.