Model a Planar Pendulum
Consider a point mass m suspended by a massless rod of length l under the influence of gravity. The position of the mass can be expressed in Cartesian coordinates by (x,y).

Modeling the System
A force balance of the mass gives the equations of motion in the x and y directions.
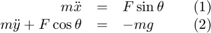
Let (u, v) be the velocities in (x, y) respectively. The system can be rewritten as a system of first order ODEs
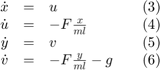
where F is the tension in the rod. The system also possesses the geometric constraint

Differentiate (7) twice with respect to time t to arrive at
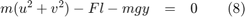
This relationship is useful since it allows F to determined at every step for use in modeling the kinematics of the system.
Simulating the System
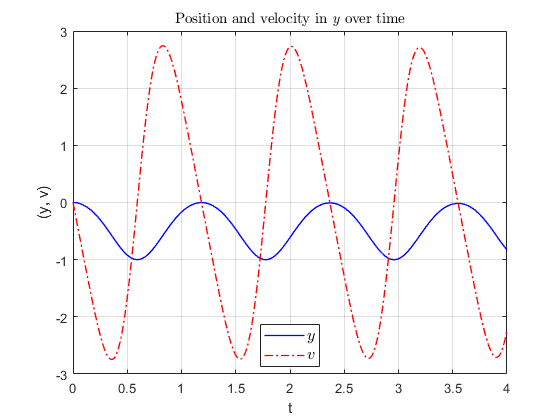
The system is simulated as shown in the figure below.

Equation (8) contains one unknown F and is of the form f(z) = 0 where 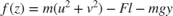 . The Algebraic Constraint block constrains f(z) to 0 and solves for F in accordance with (8).
. The Algebraic Constraint block constrains f(z) to 0 and solves for F in accordance with (8).

References
Hairer, Ernst, Christian Lubich, and Michel Roche. "The Numerical Solution Of Differential-Algebraic Systems By Runge-Kutta Methods." Lecture Notes in Mathematics. Vol. 1409, Berlin: Springer-Verlag, 1989: pp. 8-9.