Linearizing Models
The Simulink® product provides the
,
linmodlinmod2, and dlinmod functions to extract
linear state-space models from Simulink models. However, these functions provide only basic linearization
functionality. For full linearization functionality, use Simulink
Control Design™ software. For more information, see Choose Linearization Tools (Simulink Control Design).
The linmod, linmod2, and
dlinmod functions extract linear models in the form of the
state-space matrices A, B,
C, and D. State-space matrices describe
the linear input-output relationship as
where x, u, and y are state,
input, and output vectors, respectively. For example, the following model is called lmod.
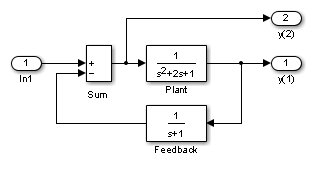
To extract the linear model of this system, enter this command.
[A,B,C,D] = linmod('lmod')
A =
-2 -1 -1
1 0 0
0 1 -1
B =
1
0
0
C =
0 1 0
0 0 -1
D =
0
1
Inputs and outputs must be defined using Inport and Outport blocks from the Ports & Subsystems library. Source and sink blocks do not act as inputs and outputs. Inport blocks can be used in conjunction with source blocks, using a Sum block. Once the data is in the state-space form or converted to an LTI object, you can apply functions in the Control System Toolbox™ product for further analysis:
Conversion to an LTI object
sys = ss(A,B,C,D);
Bode phase and magnitude frequency plot
bode(A,B,C,D) or bode(sys)
Linearized time response
step(A,B,C,D) or step(sys) impulse(A,B,C,D) or impulse(sys) lsim(A,B,C,D,u,t) or lsim(sys,u,t)
You can use other functions in the Control System Toolbox and the Robust Control Toolbox™ products for linear control system design.
When the model is nonlinear, an operating point can be chosen at which to extract the
linearized model. Extra arguments to linmod specify the operating
point.
[A,B,C,D] = linmod('sys', x, u)
For discrete systems or mixed continuous and discrete systems, use the function
dlinmod for linearization. This
function has the same calling syntax as linmod except that the second right-hand argument must contain a sample
time at which to perform the linearization.
See Also
Functions
linmod|dlinmod|linearize(Simulink Control Design) |slLinearizer(Simulink Control Design)
Apps
- Model Linearizer (Simulink Control Design)
Topics
- Choose Linearization Tools (Simulink Control Design)
- Linearize Nonlinear Models (Simulink Control Design)
- Exact Linearization Algorithm (Simulink Control Design)