Asynchronous Machine
(To be removed) Model dynamics of three-phase asynchronous machine, also known as induction machine, in SI or pu units
The Specialized Power Systems library will be removed in R2026a. Use the Simscape™ Electrical™ blocks and functions instead. For more information on updating your models, see Upgrade Specialized Power System Models to use Simscape Electrical Blocks.
Libraries:
Simscape /
Electrical /
Specialized Power Systems /
Electrical Machines
Description
The Asynchronous Machine SI Units and Asynchronous Machine pu Units blocks implement a three-phase asynchronous machine (wound rotor, squirrel cage, or double squirrel cage) modeled in a selectable dq reference frame (rotor, stator, or synchronous). Stator and rotor windings are connected in wye to an internal neutral point. The block operates in either generator or motor mode. The mode of operation is dictated by the sign of the mechanical torque:
If Tm is positive, the machine acts as a motor.
If Tm is negative, the machine acts as a generator.
The electrical part of the machine is represented by a fourth-order (or sixth-order for the double squirrel-cage machine) state-space model, and the mechanical part by a second-order system. All electrical variables and parameters are referred to the stator, which is indicated by the prime signs in the following machine equations. All stator and rotor quantities are in the arbitrary two-axis reference frame (dq frame). The subscripts used are defined in this table.
Subscript | Definition |
|---|---|
d | d-axis quantity |
q | q-axis quantity |
r | Rotor quantity (wound-rotor or single-cage) |
r1 | Cage 1 rotor quantity (double-cage) |
r2 | Cage 2 rotor quantity (double-cage) |
s | Stator quantity |
l | Leakage inductance |
m | Magnetizing inductance |
Electrical System of the Wound-Rotor or Squirrel-Cage Machine

Vqs = Rsiqs + dφqs/dt + ωφds
Vds = Rsids + dφds/dt – ωφqs
V'qr = R'ri'qr + dφ'qr/dt + (ω – ωr)φ'dr
V'dr = R'ri'dr + dφ'dr/dt – (ω – ωr)φ'qr
Te = 1.5p(φdsiqs – φqsids)

ω — Reference frame angular velocity
ωr — Electrical angular velocity
φqs = Lsiqs + Lmi'qr
φds = Lsids + Lmi'dr
φ'qr = L'ri'qr + Lmiqs
φ'dr = L'ri'dr + Lmids
Ls = Lls + Lm
L'r = L'lr + Lm
Electrical System of the Double Squirrel-Cage Machine

Vqs = Rsiqs + dφqs/dt + ωφds
Vds = Rsids + dφds/dt – ωφqs
0 = R'r1i'qr1 + dφ'qr1/dt + (ω – ωr)φ'dr1
0 = R'r1i'dr1 + dφ'dr1/dt – (ω – ωr)φ'qr1
0 = R'r2i'qr2 + dφ'qr2/dt + (ω – ωr)φ'dr2
0 = R'r2i'dr2 + dφ'dr2/dt – (ω – ωr)φ'qr2
Te = 1.5p(φdsiqs – φqsids)

φqs = Lsiqs + Lm(i'qr1 + i'qr2)
φds = Lsids + Lm(i'dr1 + i'dr2)
φ'qr1 = L'r1i'qr1 + Lmiqs
φ'dr1 = L'r1i'dr1 + Lmids
φ'qr2 = L'r2i'qr2 + Lmiqs
φ'dr2 = L'r2i'dr2 + Lmids
Ls = Lls + Lm
L'r1 = L'lr1 + Lm
L'r2 = L'lr2 + Lm
Mechanical System
The Asynchronous Machine block parameters are defined in the table. All quantities are referred to the stator.
Parameters Common to All Models | Definition |
|---|---|
Rs, Lls | Stator resistance and leakage inductance |
Lm | Magnetizing inductance |
Ls | Total stator inductance |
Vqs, iqs | q-axis stator voltage and current |
Vds, ids | d-axis stator voltage and current |
ϕqs, ϕϕds | Stator q-axis and d-axis fluxes |
ωm | Angular velocity of the rotor |
Θm | Rotor angular position |
p | Number of pole pairs |
ωr | Electrical angular velocity (ωm × p) |
Θr | Electrical rotor angular position (Θm × p) |
Te | Electromagnetic torque |
Tm | Shaft mechanical torque |
J | Combined rotor and load inertia coefficient. Set to infinite to simulate locked rotor. |
H | Combined rotor and load inertia constant. Set to infinite to simulate locked rotor. |
F | Combined rotor and load viscous friction coefficient |
Parameters Specific to Single-Cage or Wound Rotor | Definition |
|---|---|
L'r | Total rotor inductance |
R'r, L'lr | Rotor resistance and leakage inductance |
V'qr, i'qr | q-axis rotor voltage and current |
V'dr, i'dr | d-axis rotor voltage and current |
ϕ'qr, ϕ'dr | Rotor q-axis and d axis fluxes |
Parameters Specific to Double-Cage Rotor | Definition |
|---|---|
R'r1, L'lr1 | Rotor resistance and leakage inductance of cage 1 |
R'r2, L'lr2 | Rotor resistance and leakage inductance of cage 2 |
L'r1, L'r2 | Total rotor inductances of cage 1 and 2 |
i'qr1, i'qr2 | q-axis rotor current of cage 1 and 2 |
i'dr1, i'dr2 | d-axis rotor current of cage 1 and 2 |
ϕ'qr1, ϕ'dr1 | q-axis and d-axis rotor fluxes of cage 1 |
ϕ'qr2, ϕ'dr2 | q-axis and d-axis rotor fluxes of cage 2 |
Assumptions and Limitations
The Asynchronous Machine blocks do not include a representation of the saturation of leakage fluxes. Be careful when you connect ideal sources to the stator of the machine. If you choose to supply the stator via a three-phase, Y-connected infinite voltage source, you must use three sources connected in Y. However, if you choose to simulate a delta source connection, you must use only two sources connected in series.
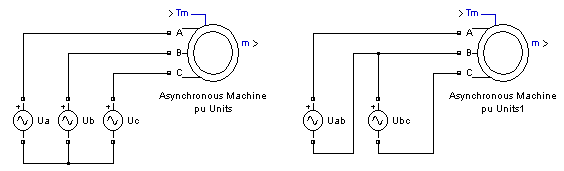
When you use Asynchronous Machine blocks in discrete systems, you might have to connect a small parasitic resistive load at the machine terminals to avoid numerical oscillations. Large sample times require larger loads. The optimum resistive load is proportional to the sample time. With a 25 μs time step on a 60 Hz system, the minimum load is approximately 2.5% of the machine nominal power. For example, a 200 MVA asynchronous machine in a power system discretized with a 50 μs sample time requires approximately 5% of resistive load or 10 MW. If the sample time is reduced to 20 μs, a resistive load of 4 MW is sufficient.
Ports
The stator terminals of the Asynchronous Machine blocks are identified by the letters A, B, and C. The rotor terminals are identified by the letters a, b, and c. The neutral connections of the stator and rotor windings are not available. Three-wire Y connections are assumed.
Input
Output
Conserving
Parameters
References
[1] Krause, P.C., O. Wasynczuk, and S.D. Sudhoff, Analysis of Electric Machinery, IEEE® Press, 2002.
[2] Mohan, N., T.M. Undeland, and W.P. Robbins, Power Electronics: Converters, Applications, and Design, John Wiley & Sons, Inc., New York, 1995, Section 8.4.1.
Extended Capabilities
Version History
Introduced before R2006a


