Peltier Device
Electrothermal cooler or thermoelectric generator
Libraries:
Simscape /
Electrical /
Sensors & Transducers
Description
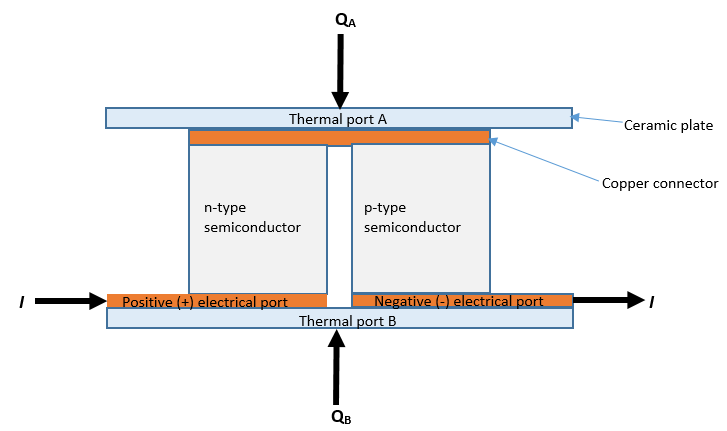
The Peltier Device block represents an electrothermal cooler or thermoelectric generator that uses the Peltier and Seebeck effects. The block converters between electrical and thermal energy:
With no current flowing, if the temperature presented at thermal port B is greater than the temperature presented at thermal port A, then there is a positive potential difference measured from the positive to the negative electrical port.
When the block acts as a cooling device, a positive current causes heat to flow from port A to port B, cooling port A relative to port B.
The defining equations are:
where:
QA is heat flow into port A.
QB is heat flow into port B.
TA is port A temperature.
TB is port B temperature.
W is electrical power (positive when flowing into the block).
V is potential difference across the + and - ports.
I is electrical current, positive from + to - port.
R is total electrical resistance.
α is Seebeck coefficient.
K is thermal conductance.
Substituting for powers and dividing all terms by current gives the electrical equation:
The block has a logging variable power_dissipated (Dissipated
power). This variable reports the DC electrical power, that is, the average
electrical power over one AC cycle if you drive the device with an AC source. In terms of
equations it is equal to the instantaneous value of
I2R and is useful in a
cooling application to indicate the nonproductive portion of the heat flow. In a heating
application, the interpretation of dissipated power is less useful.
Examples
Ports
Conserving
Parameters
Extended Capabilities
Version History
Introduced in R2018b