Multivariate Wavelet Denoising
The purpose of this example is to show the features of multivariate denoising provided in Wavelet Toolbox™.
Multivariate wavelet denoising problems deal with models of the form
where the observation X is p-dimensional, F is the deterministic signal to be recovered, and e is a spatially-correlated noise signal. This example uses a number of noise signals and performs the following steps to denoise the deterministic signal.
Loading a Multivariate Signal
To load the multivariate signal, type the following code at the MATLAB® prompt:
load ex4mwden
whosName Size Bytes Class Attributes covar 4x4 128 double x 1024x4 32768 double x_orig 1024x4 32768 double
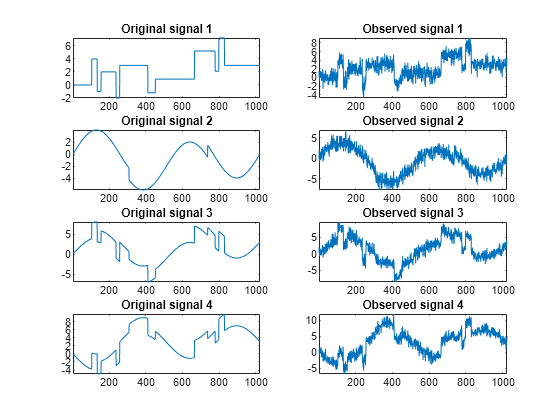
Usually, only the matrix of data x is available. Here, we also have the true noise covariance matrix covar and the original signals x_orig. These signals are noisy versions of simple combinations of the two original signals. The first signal is "Blocks" which is irregular, and the second one is "HeavySine" which is regular, except around time 750. The other two signals are the sum and the difference of the two original signals, respectively. Multivariate Gaussian white noise exhibiting strong spatial correlation is added to the resulting four signals, which produces the observed data stored in x.
Displaying the Original and Observed Signals
To display the original and observed signals, type:
kp = 0; for i = 1:4 subplot(4,2,kp+1), plot(x_orig(:,i)); axis tight; title(['Original signal ',num2str(i)]) subplot(4,2,kp+2), plot(x(:,i)); axis tight; title(['Observed signal ',num2str(i)]) kp = kp + 2; end
The true noise covariance matrix is given by:
covar
covar = 4×4
1.0000 0.8000 0.6000 0.7000
0.8000 1.0000 0.5000 0.6000
0.6000 0.5000 1.0000 0.7000
0.7000 0.6000 0.7000 1.0000
Removing Noise by Simple Multivariate Thresholding
The denoising strategy combines univariate wavelet denoising in the basis, where the estimated noise covariance matrix is diagonal with noncentered Principal Component Analysis (PCA) on approximations in the wavelet domain or with final PCA.
First, perform univariate denoising by typing the following lines to set the denoising parameters:
level = 5; wname = 'sym4'; tptr = 'sqtwolog'; sorh = 's';
Then, set the PCA parameters by retaining all the principal components:
npc_app = 4; npc_fin = 4;
Finally, perform multivariate denoising by typing:
x_den = wmulden(x, level, wname, npc_app, npc_fin, tptr, sorh);
Displaying the Original and Denoised Signals
To display the original and denoised signals type the following:
clf kp = 0; for i = 1:4 subplot(4,3,kp+1), plot(x_orig(:,i)); axis tight; title(['Original signal ',num2str(i)]) subplot(4,3,kp+2), plot(x(:,i)); axis tight; title(['Observed signal ',num2str(i)]) subplot(4,3,kp+3), plot(x_den(:,i)); axis tight; title(['Denoised signal ',num2str(i)]) kp = kp + 3; end

Improving the First Result by Retaining Fewer Principal Components
We can see that, overall, the results are satisfactory. Focusing on the two first signals, note that they are correctly recovered, but we can improve the result by taking advantage of the relationships between the signals, leading to an additional denoising effect.
To automatically select the numbers of retained principal components using Kaiser's rule, which retains components associated with eigenvalues exceeding the mean of all eigenvalues, type:
npc_app = 'kais'; npc_fin = 'kais';
Perform multivariate denoising again by typing:
[x_den, npc, nestco] = wmulden(x, level, wname, npc_app, ...
npc_fin, tptr, sorh);Displaying the Number of Retained Principal Components
The second output argument npc is the number of retained principal components for PCA for approximations and for final PCA.
npc
npc = 1×2
2 2
As expected, because the signals are combinations of two original signals, Kaiser's rule automatically detects that only two principal components are of interest.
Displaying the Estimated Noise Covariance Matrix
The third output argument nestco contains the estimated noise covariance matrix:
nestco
nestco = 4×4
1.0784 0.8333 0.6878 0.8141
0.8333 1.0025 0.5275 0.6814
0.6878 0.5275 1.0501 0.7734
0.8141 0.6814 0.7734 1.0967
As it can be seen by comparing it with the true matrix covar given previously, the estimation is satisfactory.
Displaying the Original and Final Denoised Signals
To display the original and final denoised signals type:
kp = 0; for i = 1:4 subplot(4,3,kp+1), plot(x_orig(:,i)); axis tight; title(['Original signal ',num2str(i)]) subplot(4,3,kp+2), plot(x(:,i)); axis tight; title(['Observed signal ',num2str(i)]) subplot(4,3,kp+3), plot(x_den(:,i)); axis tight; title(['Denoised signal ',num2str(i)]) kp = kp + 3; end
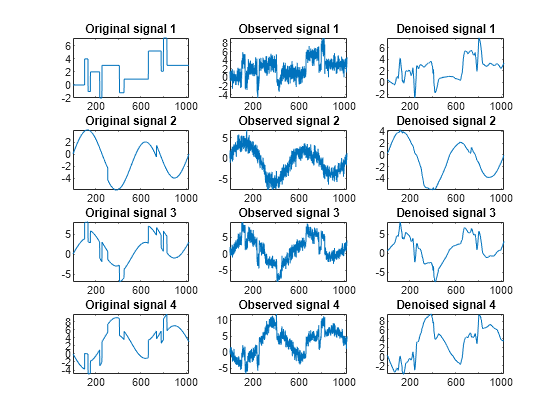
These results are better than those previously obtained. The first signal, which is irregular, is still correctly recovered, while the second signal, which is more regular, is better denoised after this second stage of PCA.
Learning More About Multivariate Denoising
You can find more information about multivariate denoising, including some theory, simulations, and real examples, in the following reference:
M. Aminghafari, N. Cheze and J-M. Poggi (2006), "Multivariate denoising using wavelets and principal component analysis," Computational Statistics & Data Analysis, 50, pp. 2381-2398.
