dddtree2
Dual-tree and double-density 2-D wavelet transform
Syntax
Description
wt = dddtree2(typetree,x,level,fdf,df)typetree discrete wavelet transform of the 2-D input image,
x, down to level, level. The wavelet transform
uses the decomposition (analysis) filters, fdf, for the first level and
the analysis filters, df, for subsequent levels. Supported wavelet
transforms are the critically sampled DWT, double-density, real oriented dual-tree, complex
oriented dual-tree, real oriented dual-tree double-density, and complex oriented dual-tree
double-density wavelet transform. The critically sampled DWT is a filter bank decomposition
in an orthogonal or biorthogonal basis (nonredundant). The other wavelet transforms are
oversampled filter banks with differing degrees of directional selectivity.
wt = dddtree2(typetree,x,level,fname1,fname2)fname1 for the first stage of the
dual-tree wavelet transform and the filters specified in fname2 for
subsequent stages of the dual-tree wavelet transform. Specifying different filters for stage
1 is valid and necessary only when typetree is
'realdt', 'cplxdt', 'realdddt',
or 'cplxdddt'.
Examples
Visualize the six directional wavelets of the real oriented dual-tree wavelet transform.
Create the first-stage Farras analysis filters for the two trees.
Faf{1} = [0 0
-0.0884 -0.0112
0.0884 0.0112
0.6959 0.0884
0.6959 0.0884
0.0884 -0.6959
-0.0884 0.6959
0.0112 -0.0884
0.0112 -0.0884
0 0];
Faf{2} = [ 0.0112 0
0.0112 0
-0.0884 -0.0884
0.0884 -0.0884
0.6959 0.6959
0.6959 -0.6959
0.0884 0.0884
-0.0884 0.0884
0 0.0112
0 -0.0112];Create the 6-tap Kingsbury Q-shift analysis filters for subsequent stages of the multiresolution analysis.
af{1} = [ 0.0352 0
0 0
-0.0883 -0.1143
0.2339 0
0.7603 0.5875
0.5875 -0.7603
0 0.2339
-0.1143 0.0883
0 0
0 -0.0352];
af{2} = [0 -0.0352
0 0
-0.1143 0.0883
0 0.2339
0.5875 -0.7603
0.7603 0.5875
0.2339 0
-0.0883 -0.1143
0 0
0.0352 0];To visualize the six directional wavelets, you will modify the wavelet coefficients of a four level real oriented dual-tree wavelet transform of an image of zeros. Create an image of zeros whose size satisfies the following constraints:
The row and column dimensions are divisible by .
The minimum of the row and column size must be greater than or equal to the product of the maximum length of the analysis filters and .
J = 4; L = 3*2^(J+1); N = L/2^J; x = zeros(2*L,3*L); [numrows,numcols] = size(x)
numrows = 192
numcols = 288
Obtain the real oriented dual-tree wavelet transform of the image of zeros down to level 4.
wt = dddtree2('realdt',x,J,Faf,af)wt = struct with fields:
type: 'realdt'
level: 4
filters: [1×1 struct]
cfs: {[96×144×3×2 double] [48×72×3×2 double] [24×36×3×2 double] [12×18×3×2 double] [12×18×2 double]}
sizes: [14×2 double]
The fourth element in wt.cfs are the level 4 wavelet coefficients. Insert a 1 in one position of the six wavelet subbands (three orientations two trees) at the coarsest scale, and invert the wavelet transform.
wt.cfs{4}(N/2,N/2+0*N,1,1) = 1;
wt.cfs{4}(N/2,N/2+1*N,2,1) = 1;
wt.cfs{4}(N/2,N/2+2*N,3,1) = 1;
wt.cfs{4}(N/2+N,N/2+0*N,1,2) = 1;
wt.cfs{4}(N/2+N,N/2+1*N,2,2) = 1;
wt.cfs{4}(N/2+N,N/2+2*N,3,2) = 1;
xrec = idddtree2(wt);Visualize the six directional wavelets.
imagesc(xrec); colormap gray; axis off; title('Real Oriented Dual-Tree Wavelets')

Obtain the double-density wavelet transform of an image.
Load the image and obtain the double-density wavelet transform using 6-tap filters (see dtfilters).
load xbox imagesc(xbox) colormap gray

wt = dddtree2('ddt',xbox,1,'filters1')
wt = struct with fields:
type: 'ddt'
level: 1
filters: [1×1 struct]
cfs: {[64×64×8 double] [64×64 double]}
sizes: [10×2 double]
In the critically sampled 2-D discrete wavelet transform, there is one highpass filter. Filtering the rows and columns of the image with the highpass filter corresponds to extracting details in the diagonal orientation. In the double-density wavelet transform, there are two highpass filters, H1 and H2. Diagonally oriented details are extracted by filtering the image rows and columns with four combinations of the highpass filters. Visualize the diagonal details in the four wavelet highpass-highpass subbands.
H1H1 = wt.cfs{1}(:,:,4);
H1H2 = wt.cfs{1}(:,:,5);
H2H1 = wt.cfs{1}(:,:,7);
H2H2 = wt.cfs{1}(:,:,8);
subplot(2,2,1)
imagesc(H1H1);
title('H1 H1')
colormap gray;
subplot(2,2,2);
imagesc(H1H2);
title('H1 H2')
subplot(2,2,3)
imagesc(H2H1)
title('H2 H1')
subplot(2,2,4)
imagesc(H2H2)
title('H2 H2')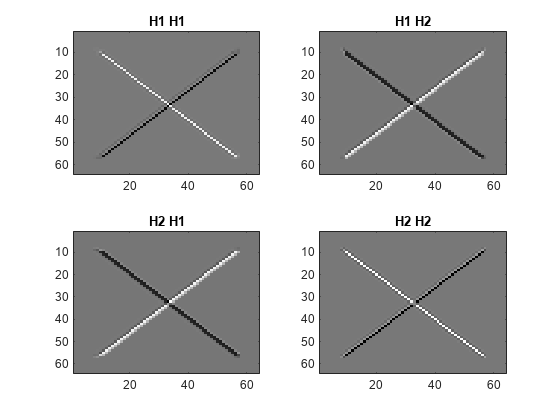
Obtain the complex dual-tree wavelet transform of an image. Show that the complex dual-tree wavelet transform can detect the two different diagonal directions.
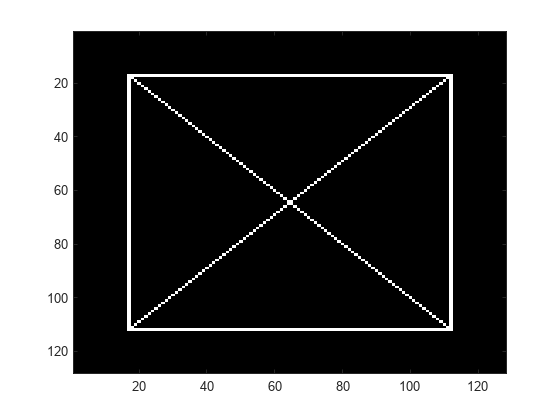
Load the image and obtain the complex dual-tree wavelet transform.
load xbox imagesc(xbox) colormap gray
wt = dddtree2('cplxdt',xbox,1,'FSfarras','qshift10')
wt = struct with fields:
type: 'cplxdt'
level: 1
filters: [1×1 struct]
cfs: {[5-D double] [64×64×2×2 double]}
sizes: [5×2 double]
Obtain and display the diagonally oriented details from the two trees.
waveletcfs = wt.cfs{1};
subplot(2,2,1)
imagesc(waveletcfs(:,:,3,1,1))
title('Diagonal - Tree 1 - Real')
colormap gray
subplot(2,2,2)
imagesc(waveletcfs(:,:,3,1,2))
title('Diagonal - Tree 1 - Imaginary')
subplot(2,2,3)
imagesc(waveletcfs(:,:,3,2,1))
title('Diagonal - Tree 2 - Real')
subplot(2,2,4)
imagesc(waveletcfs(:,:,3,2,2))
title('Diagonal - Tree 2 - Imaginary')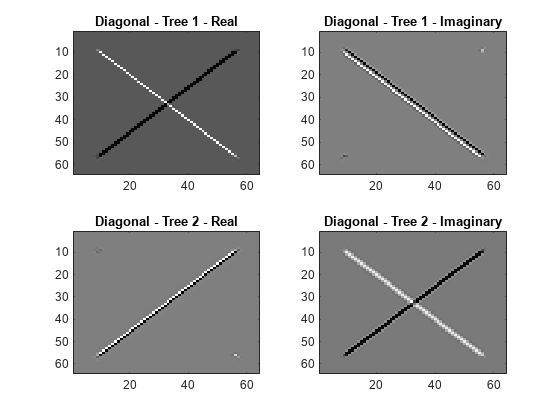
Input Arguments
Type of wavelet decomposition, specified as one of 'dwt',
'ddt', 'realdt', 'cplxdt',
'realdddt', or 'cplxdddt'. The type,
'dwt', produces a critically sampled (nonredundant) discrete
wavelet transform. The other decomposition types produce oversampled wavelet transforms.
'ddt' produces a double-density wavelet transform with one scaling
and two wavelet filters for both row and column filtering. The double-density wavelet
transform uses the same filters at all stages. 'realdt' and
'cplxdt' produce oriented dual-tree wavelet transforms consisting
of two and four separable wavelet transforms. 'realdddt' and
'cplxdddt' produce double-density dual-tree wavelet transforms. The
dual-tree wavelet transforms use different filters for the first stage (level).
Input image, specified as a matrix with even-length row and column dimensions. Both the row and column dimensions must be divisible by 2L, where L is the level of the wavelet transform. Additionally, the minimum of the row and column dimensions of the image must be greater than or equal to the product of the maximum length of the decomposition (analysis) filters and 2(L-1).
Data Types: double
Level of the wavelet decomposition, specified as a positive
integer. If L is the value of level,
2L must divide both
the row and column dimensions of x. Additionally,
the minimum of the row and column dimensions of the image must be
greater than or equal to the product of the maximum length of the
decomposition (analysis) filters and 2(L-1).
The level-one analysis filters, specified as a matrix or cell
array of matrices. Specify fdf as a matrix when typetree is 'dwt' or 'ddt'.
The size and structure of the matrix depend on the typetree input
as follows:
'dwt'— This is the critically sampled discrete wavelet transform. In this case,fdfis a two-column matrix with the lowpass (scaling) filter in the first column and the highpass (wavelet) filter in the second column.'ddt'— This is the double-density wavelet transform. The double-density DWT is a three-channel perfect reconstruction filter bank.fdfis a three-column matrix with the lowpass (scaling) filter in the first column and the two highpass (wavelet) filters in the second and third columns. In the double-density wavelet transform, the single lowpass and two highpass filters constitute a three-channel perfect reconstruction filter bank. This is equivalent to the three filters forming a tight frame. You cannot arbitrarily choose the two wavelet filters in the double-density DWT. The three filters together must form a tight frame.
Specify fdf as a 1-by-2 cell array of matrices
when typetree is a dual-tree transform, 'realdt', 'cplxdt', 'realdddt',
or 'cplxdddt'. The size and structure of the matrix
elements in the cell array depend on the typetree input
as follows:
For the dual-tree complex wavelet transforms,
'realdt'and'cplxdt',fdf{1}is an N-by-2 matrix containing the lowpass (scaling) and highpass (wavelet) filters for the first tree andfdf{2}is an N-by-2 matrix containing the lowpass (scaling) and highpass (wavelet) filters for the second tree.For the double-density dual-tree complex wavelet transforms,
'realdddt'and'cplxdddt',fdf{1}is an N-by-3 matrix containing the lowpass (scaling) and two highpass (wavelet) filters for the first tree andfdf{2}is an N-by-3 matrix containing the lowpass (scaling) and two highpass (wavelet) filters for the second tree.
Analysis filters for levels > 1, specified as a matrix or
cell array of matrices. Specify df as a matrix
when typetree is 'dwt' or 'ddt'.
The size and structure of the matrix depend on the typetree input
as follows:
'dwt'— This is the critically sampled discrete wavelet transform. In this case,dfis a two-column matrix with the lowpass (scaling) filter in the first column and the highpass (wavelet) filter in the second column. For the critically sampled orthogonal or biorthogonal DWT, the filters indfandfdfmust be identical.'ddt'— This is the double-density wavelet transform. The double-density DWT is a three-channel perfect reconstruction filter bank.dfis a three-column matrix with the lowpass (scaling) filter in the first column and the two highpass (wavelet) filters in the second and third columns. In the double-density wavelet transform, the single lowpass and two highpass filters constitute a three-channel perfect reconstruction filter bank. This is equivalent to the three filters forming a tight frame. For the double-density DWT, the filters indfandfdfmust be identical.
Specify df as a 1-by-2 cell array of matrices
when typetree is a dual-tree transform, 'realdt', 'cplxdt', 'realdddt',
or 'cplxdddt'. For dual-tree transforms, the filters
in fdf and df must be different.
The size and structure of the matrix elements in the cell array depend
on the typetree input as follows:
For the dual-tree wavelet transforms,
'realdt'and'cplxdt',df{1}is an N-by-2 matrix containing the lowpass (scaling) and highpass (wavelet) filters for the first tree anddf{2}is an N-by-2 matrix containing the lowpass (scaling) and highpass (wavelet) filters for the second tree.For the double-density dual-tree complex wavelet transforms,
'realdddt'and'cplxdddt',df{1}is an N-by-3 matrix containing the lowpass (scaling) and two highpass (wavelet) filters for the first tree anddf{2}is an N-by-3 matrix containing the lowpass (scaling) and two highpass (wavelet) filters for the second tree.
First-stage filter name, specified as a character vector or string scalar. Specifying a
first-level filter that is different from the wavelet and scaling filters in
subsequent levels is valid and necessary only with the dual-tree wavelet
transforms, 'realdt', 'cplxdt',
'realdddt', and 'cplxdddt'.
Filter name for stages > 1, specified as a character vector or string scalar. Specifying a
different filter for stages > 1 is valid and necessary only with the
dual-tree wavelet transforms, 'realdt',
'cplxdt', 'realdddt', and
'cplxdddt'.
Output Arguments
Wavelet transform, returned as a structure with these fields:
Type of wavelet decomposition used in the analysis returned
as one of 'dwt', 'ddt', 'realdt', 'cplxdt', 'realdddt',
or 'cplxdddt'. 'dwt' is the
critically sampled DWT. 'ddt' produces a double-density
wavelet transform with one scaling and two wavelet filters for both
row and column filtering. 'realdt' and 'cplxdt' produce
oriented dual-tree wavelet transforms consisting of 2 and 4 separable
wavelet transforms. 'realdddt' and 'cplxdddt' produce
double-density dual-tree wavelet transforms consisting of two and
four separable wavelet transforms.
Level of wavelet decomposition, returned as a positive integer.
Decomposition (analysis) and reconstruction (synthesis) filters, returned as a structure with these fields:
First-stage analysis filters, returned as an N-by-2 or N-by-3 matrix for single-tree wavelet transforms, or a 1-by-2 cell array of two N-by-2 or N-by-3 matrices for dual-tree wavelet transforms. The matrices are N-by-3 for the double-density wavelet transforms. For an N-by-2 matrix, the first column of the matrix is the scaling (lowpass) filter and the second column is the wavelet (highpass) filter. For an N-by-3 matrix, the first column of the matrix is the scaling (lowpass) filter and the second and third columns are the wavelet (highpass) filters. For the dual-tree transforms, each element of the cell array contains the first-stage analysis filters for the corresponding tree.
Analysis filters for levels > 1, returned as an N-by-2 or N-by-3 matrix for single-tree wavelet transforms, or a 1-by-2 cell array of two N-by-2 or N-by-3 matrices for dual-tree wavelet transforms. The matrices are N-by-3 for the double-density wavelet transforms. For an N-by-2 matrix, the first column of the matrix is the scaling (lowpass) filter and the second column is the wavelet (highpass) filter. For an N-by-3 matrix, the first column of the matrix is the scaling (lowpass) filter and the second and third columns are the wavelet (highpass) filters. For the dual-tree transforms, each element of the cell array contains the analysis filters for the corresponding tree.
First-level reconstruction filters, returned as an N-by-2 or N-by-3 matrix for single-tree wavelet transforms, or a 1-by-2 cell array of two N-by-2 or N-by-3 matrices for dual-tree wavelet transforms. The matrices are N-by-3 for the double-density wavelet transforms. For an N-by-2 matrix, the first column of the matrix is the scaling (lowpass) filter and the second column is the wavelet (highpass) filter. For an N-by-3 matrix, the first column of the matrix is the scaling (lowpass) filter and the second and third columns are the wavelet (highpass) filters. For the dual-tree transforms, each element of the cell array contains the first-stage synthesis filters for the corresponding tree.
Reconstruction filters for levels > 1, returned as an N-by-2 or N-by-3 matrix for single-tree wavelet transforms, or a 1-by-2 cell array of two N-by-2 or N-by-3 matrices for dual-tree wavelet transforms. The matrices are N-by-3 for the double-density wavelet transforms. For an N-by-2 matrix, the first column of the matrix is the scaling (lowpass) filter and the second column is the wavelet (highpass) filter. For an N-by-3 matrix, the first column of the matrix is the scaling (lowpass) filter and the second and third columns are the wavelet (highpass) filters. For the dual-tree transforms, each element of the cell array contains the first-stage analysis filters for the corresponding tree.
Wavelet transform coefficients, specified as a
1-by-(level+1) cell array of matrices. The size and
structure of the matrix elements of the cell array depend on the type of wavelet
transform, typetree as follows:
'dwt'—cfs{j}(:,:,d)j = 1,2,...
levelis the level.d = 1,2,3 is the orientation.
cfs{level+1}(:,:)are the lowpass, or scaling, coefficients.
'ddt'—cfs{j}(:,:,d)j = 1,2,...
levelis the level.d = 1,2,3,4,5,6,7,8 is the orientation.
cfs{level+1}(:,:)are the lowpass, or scaling, coefficients.
'realdt'—cfs{j}(:,:,d,k)j = 1,2,...
levelis the level.d = 1,2,3 is the orientation.
k = 1,2 is the wavelet transform tree.
cfs{level+1}(:,:,k)are the lowpass, or scaling, coefficients.
'cplxdt'—cfs{j}(:,:,d,k,m)j = 1,2,...
levelis the level.d = 1,2,3 is the orientation.
k = 1,2 is the wavelet transform tree.
m = 1,2 are the real and imaginary parts.
cfs{level+1}(:,:,k,m)are the lowpass, or scaling, coefficients.
'realdddt'—cfs{j}(:,:,d,k)j = 1,2,...
levelis the level.d = 1,2,3,4,5,6,7,8 is the orientation.
k = 1,2 is the wavelet transform tree.
cfs{level+1}(:,:,k)are the lowpass, or scaling, coefficients.
'cplxdddt'—cfs{j}(:,:,d,k,m)j = 1,2,...
levelis the level.d = 1,2,3,4,5,6,7,8 is the orientation.
k = 1,2 is the wavelet transform tree.
m = 1,2 are the real and imaginary parts.
cfs{level+1}(:,:,k,m)are the lowpass, or scaling, coefficients.
Each orientation corresponds to a particular subband. The double-density
transforms 'ddt', 'realdddt', and
'cplxdddt' generate wavelet coefficients of eight
orientations. The other transforms, 'dwt',
'realdt', and 'cplxdt' generate wavelet
coefficients of three orientations. The correspondence to subbands is as
follows.
typetree | Orientations |
|---|---|
'dwt', 'realdt',
'cplxdt' |
|
'ddt', 'realdddt',
'cplxdddt' |
|
Sizes of components in cfs, returned as an N-by-2
integer-valued matrix. The value of N depends on the level of wavelet
decomposition and the type of wavelet decomposition: N = 2 +
level × (number of orientations).
cfs(1,:)= dimensions of input image.cfs(2+level,:)= dimensions of scaling coefficients.cfs(1+no×(i–1)+(1:no),:)= dimensions of levelidetail coefficients, wherenois the number of orientations.
Version History
Introduced in R2013b
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)