OFDM with FFT Based Oversampling
This example modifies an OFDM+CP signal to efficiently output an oversampled waveform from the OFDM modulator. Configure the simple case with the sample rate related to subcarrier spacing and FFT length.
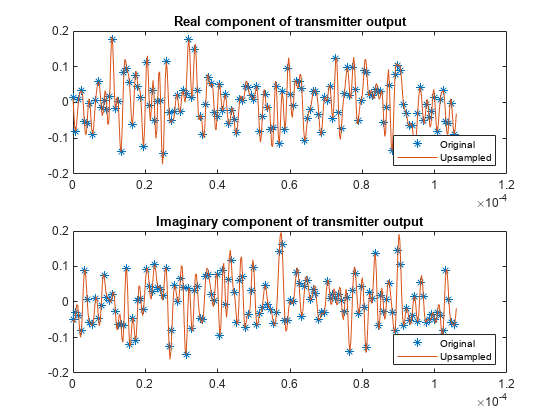
k = 4; % Number of bits per symbol M = 2^k; % Modulation order nFFT = 128; % Number of FFT bins cplen = 8; % CP length txsymbols = randi([0 M-1],nFFT,1); txgrid = qammod(txsymbols,M,UnitAveragePower=true); txout = ifft(txgrid,nFFT); txout = txout(:); % Vectorize matrix if processing multiple symbols txcp = txout(nFFT-cplen+1:nFFT); txout = [txcp; txout]; scs = 20e3; % Subcarrier spacing in Hz Fs = scs * nFFT/2; % Sampling rate (1.28e6 Hz) Ts = 1 / Fs; % Sample duration in seconds Tend = Ts * (length(txout)-1); subplot(211) hold off plot(0:Ts:Tend,real(txout),"*") title("Real component of transmitter output") subplot(212) hold off plot(0:Ts:Tend,imag(txout),"*") title("Imaginary component of transmitter output")
Define an FFT length longer than nFFT to cause oversampling in time domain. To aid comparison later, insert zeros into the middle of txgrid to maintain correspondence between bin centers for the original and upsampled signals. A control here allows you to adjust the integer oversampling rate used by the OFDM modulator output and demodulator input.
upFactor =3; nFFTUp = upFactor * nFFT; fftgrid = [txgrid(1:nFFT/2); ... zeros((upFactor-1)*nFFT,1); ... txgrid((nFFT/2+1):nFFT)]; % Each column of fftgrid is one OFDM symbol txout = upFactor * ifft(fftgrid,nFFTUp); % Vectorize the matrix to process multiple OFDM symbols txout = txout(:); cplenUp = cplen * upFactor; txcp = txout(nFFTUp-cplenUp+1:nFFTUp); txout = [txcp; txout]; Ts = 1 / (upFactor*Fs); Tend = Ts * (length(txout)-1); subplot(211) hold on plot(0:Ts:Tend,real(txout)) legend ("Original","Upsampled","Location","southeast") subplot(212) hold on plot(0:Ts:Tend,imag(txout)) legend ("Original","Upsampled","Location","southeast")
Filter the transmission through a channel that adds noise, frequency dependency, and delay to the received signal.
hchan = [0.4 1 0.4].'; rxin = awgn(txout,40); % Add noise rxin = conv(rxin,hchan); % Add frequency dependency channelDelay = dsp.Delay(1); % Could use fractional delay rxin = channelDelay(rxin); % Add delay
Add a random offset less than the CP length. An offset setting of zero models perfect synchronization between transmitted and received signals. Any timing offset less than the CP length can be compensated by equalization via an additional linear phase. To directly compare signals at different rates, prior to the FFT processing, normalize the synchronized signal by the upsampling factor.
offset = (randi(cplenUp) - 1); % random offset less than length of CP % Remove CP and synchronize the received signal rxsync = rxin(cplenUp+1+channelDelay.Length-offset:end); rxgrid = fft(rxsync(1:nFFTUp),nFFTUp)/upFactor;
Practical systems require estimation of the channel as part of the signal recovery process. The combination of OFDM and a CP simplifies equalization to a complex scalar for each frequency bin. As long as the latency falls within the length of the CP, synchronization is accomplished by the channel estimator. A control here allows you to experiment by disabling the equalization at the receiver front end.
useEqualizer =true; if useEqualizer hfchan = fft(hchan,nFFTUp); % Linear phase term related to timing offset offsetf = exp(-1i * 2*pi*offset * (0:nFFTUp-1).'/nFFTUp); rxgrideq = rxgrid ./ (hfchan .* offsetf); else % Without equalization errors occur rxgrideq = rxgrid; end rxgridNoZeroPad = [rxgrideq(1:nFFT/2); ... rxgrideq((1+(upFactor-0.5)*nFFT):end)]; rxsymbols = qamdemod(rxgridNoZeroPad,M,UnitAveragePower=true); if max(txsymbols - rxsymbols) < 1e-8 disp("Oversampled receiver output matches transmitter input."); else disp("Received symbols do not match transmitted symbols.") end
Oversampled receiver output matches transmitter input.