chbpnt
Chebyshev-Demko points
Syntax
tau = chbpnt(t,k)
chbpnt(t,k,tol)
[tau,sp] = chbpnt(...)
Description
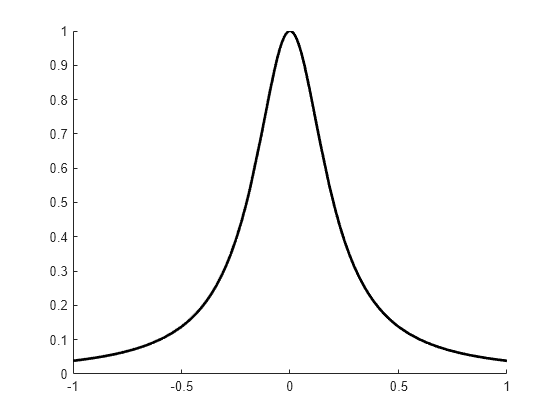
tau = chbpnt(t,k) are the extreme sites of the
Chebyshev spline of order k with knot sequence t.
These are particularly good sites at which to interpolate data by splines of order
k with knot sequence t because the resulting
interpolant is often quite close to the best uniform approximation from that spline
space to the function whose values at tau are being
interpolated.
chbpnt(t,k,tol) also specifies the tolerance tol to be used in the iterative process that constructs the Chebyshev spline. This process is terminated when the relative difference between the absolutely largest and the absolutely smallest local extremum of the spline is smaller than tol. The default value for tol is .001.
[tau,sp] = chbpnt(...) also returns, in sp, the Chebyshev spline.
Examples
Algorithms
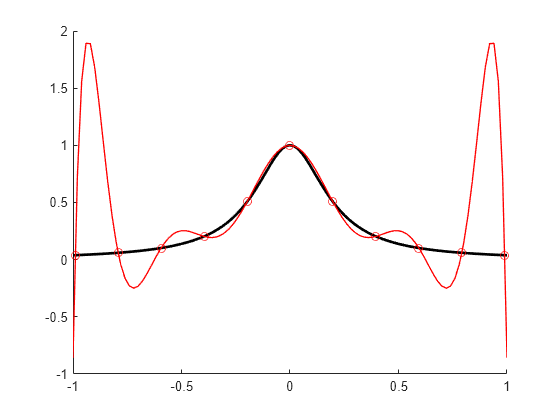
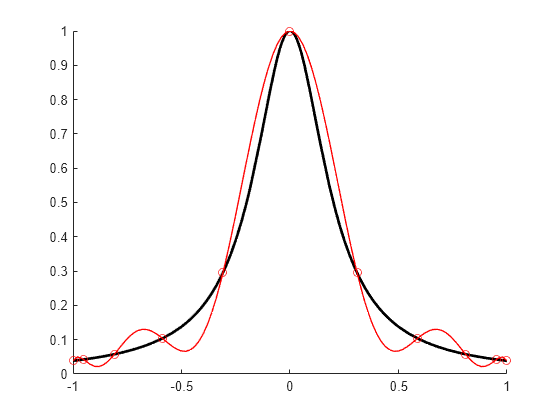
The Chebyshev spline for the given knot sequence and order is constructed iteratively, using
the Remez algorithm, using as initial guess the spline that takes alternately the values
1 and −1 at the sequence aveknt(t,k). The example Construct Chebyshev Spline gives a detailed discussion of one
version of the process as applied to a particular example.