stmak
Put together function in stform
Syntax
stmak(centers,coefs)
st = stmak(centers,x,type)
st = stmak(centers,coefs,type,interv)
Description
stmak(centers,coefs) returns the stform
of the function f given by
with
the thin-plate spline basis function, and with |x| denoting the Euclidean norm of the vector x.
centers and coefs must be matrices with the
same number of columns.
st = stmak(centers,x,type) stores in
st the stform of the function f given
by
with the ψj as
indicated by the character vector or string scalar type, which
can be one of the following:
'tp00', for the thin-plate spline;'tp10', for the first derivative of a thin-plate spline with respect to its first argument;'tp01', for the first derivative of a thin-plate spline with respect to its second argument;'tp', the default.
Here are the details.
| ψj(x)
= φ(|x –
cj|2),
cj
with φ(t) = tlog(t) ψn–2(x) = x(1) ψn–1(x) = x(2) ψn(x) = 1 |
| ψj(x)
= φ(|x –
cj|2),
cj
with φ(t) = (D1t)(logt + 1), and D1t the partial derivative of t = t(x) = |x – cj|2 with respect to x(1) ψn(x) = 1 |
| ψj(x)
= φ(|x –
cj|2),
cj
with φ(t) = (D2t)(logt + 1), and D2t the partial derivative of t = t(x) = |x – cj|2 with respect to x(2) ψn(x) = 1 |
| ψj(x)
= φ(|x –
cj|2),
cj
with φ(t) = tlog(t) |
st = stmak(centers,coefs,type,interv)
also specifies the basic interval for the stform, with interv{j}
specifying, in the form [a,b], the range of the
jth variable. The default for interv is
the smallest such box that contains all the given centers.
Examples
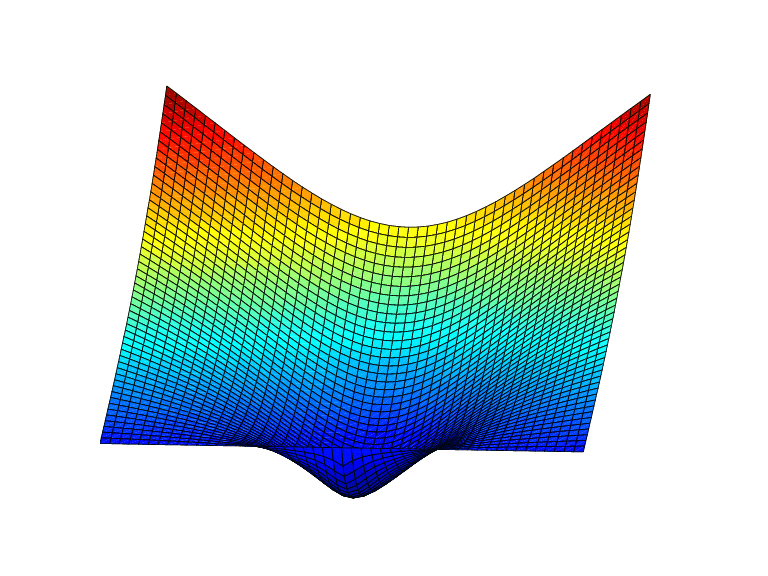
Example 1. The following generates the figure below, of the thin-plate spline basis function, but suitably restricted to show that this function is negative near the origin. For this, the extra lines are there to indicate the zero level.
inx = [-1.5 1.5]; iny = [0 1.2];
fnplt(stmak([0;0],1),{inx,iny})
hold on, plot(inx,repmat(linspace(iny(1),iny(2),11),2,1),'r')
view([25,20]),axis off, hold off

Example 2. We now also generate and plot, on the very same domain, the first partial derivative D2ψ of the thin-plate spline basis function, with respect to its second argument.
inx = [-1.5 1.5]; iny = [0 1.2];
fnplt(stmak([0;0],[1 0],'tp01',{inx,iny}))
view([13,10]),shading flat,axis off
Note that, this time, we have explicitly set the basic interval for the stform.
The resulting figure, below, shows a very strong variation near the origin. This reflects the fact that the second derivatives of ψ have a logarithmic singularity there.