designFracDelayFIR
Syntax
Description
h = designFracDelayFIRh is the vector
of filter coefficients.
h = designFracDelayFIR(Name=Value)
For example, h =
designFracDelayFIR(FractionalDelay=0.3,Bandwidth=0.6)SystemObject argument is true, the
function returns a dsp.FIRFilter object.
When you specify any of the numeric input arguments in single precision, the function
designs the filter coefficients in single precision. Alternatively, you can use the Datatype and
like arguments to control the coefficients data
type. (since R2024b)
Examples
Design a fractional delay FIR filter using the designFracDelayFIR function. Pass the delay and the filter length as the input arguments to the function. Vary the filter length and observe the effect on the measured combined bandwidth and the nominal group delay.
Vary Filter Length
Set delay to 0.25 and filter length to 8 and design the fractional delay FIR filter.
fd = 0.25; [h1,i10,bw1] = designFracDelayFIR(FractionalDelay=fd,FilterLength=8)
h1 = 1×8
-0.0086 0.0417 -0.1355 0.8793 0.2931 -0.0968 0.0341 -0.0074
i10 = 3
bw1 = 0.5810
The nominal group delay of the filter i10+fd equals 3.25 samples. The measured combined bandwidth of the filter is 0.5810 in normalized frequency units.
Repeat the process with a filter length of 32 taps.
[h2,i20,bw2] = designFracDelayFIR(FractionalDelay=fd,FilterLength=32)
h2 = 1×32
-0.0001 0.0004 -0.0009 0.0017 -0.0029 0.0046 -0.0071 0.0104 -0.0148 0.0208 -0.0291 0.0410 -0.0594 0.0926 -0.1752 0.8983 0.2994 -0.1252 0.0758 -0.0515 0.0367 -0.0266 0.0193 -0.0139 0.0098 -0.0067 0.0044 -0.0028 0.0016 -0.0009 0.0004 -0.0001
i20 = 15
bw2 = 0.8571
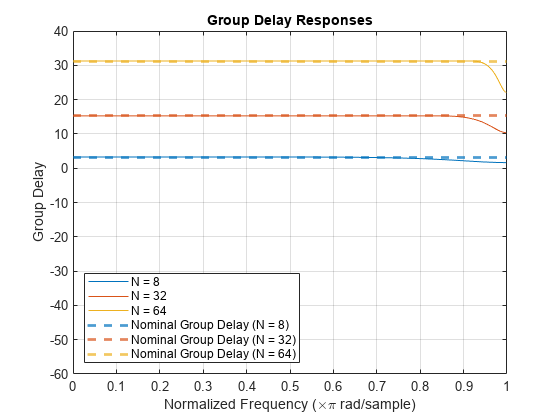
The nominal group delay of the filter now equals 15.25 samples. By increasing the filter length, the integer latency i0 increases, resulting in an increase in the nominal group delay. The combined bandwidth of the filter also increases to 0.8571 in normalized frequency units.
Increase the filter length to 64 taps. The group delay increases to 31.25 samples, and the integer latency is 31 samples. The measured combined bandwidth of the filter further increases to 0.9219, covering 92.19% of the overall bandwidth. As the filter length continues to increase, the combined bandwidth tends closer towards 1.
[h3,i30,bw3] = designFracDelayFIR(FractionalDelay=fd,FilterLength=64)
h3 = 1×64
-0.0000 0.0001 -0.0001 0.0002 -0.0003 0.0004 -0.0006 0.0008 -0.0010 0.0013 -0.0017 0.0022 -0.0027 0.0034 -0.0042 0.0051 -0.0061 0.0074 -0.0088 0.0105 -0.0125 0.0149 -0.0177 0.0212 -0.0255 0.0311 -0.0386 0.0494 -0.0664 0.0979 -0.1787 0.8997 0.2999 -0.1277 0.0801 -0.0575 0.0442 -0.0352 0.0288 -0.0239 0.0200 -0.0168 0.0142 -0.0120 0.0101 -0.0085 0.0071 -0.0059 0.0049 -0.0040
i30 = 31
bw3 = 0.9219
Plot Magnitude Response
Plot the magnitude response of the three filters. Mark the measured combined bandwidth (MBW) of the three filters. By increasing the filter length, you can see that the measured combined bandwidth increases.
[H1,w] = freqz(h1,1); H2 = freqz(h2,1); H3 = freqz(h3,1); figure; plot(w/pi,mag2db(abs([H1 H2 H3]))) hold on hline = lines; xline(bw1, LineStyle = '--', LineWidth = 2, Color = hline(1,:)) xline(bw2, LineStyle = '--', LineWidth = 2, Color = hline(2,:)) xline(bw3, LineStyle = '--', LineWidth = 2, Color = hline(3,:)) hold off title('Magnitude Responses in dB') xlabel("Normalized Frequency (\times\pi rad/sample)") ylabel("Magnitude (dB)") grid legend('N = 8','N = 32','N = 64',... 'MBW (N = 8)',... 'MBW (N = 32)',... 'MBW (N = 64)',Location='southwest')

Plot Group Delay Response
Plot the group delay response of the three filters. Mark the nominal group delay i0 + fd of the three filters. By increasing the filter length, you can see that the nominal group delay increases.
[g1,w] = grpdelay(h1,1); g2 = grpdelay(h2,1); g3 = grpdelay(h3,1); figure; plot(w/pi,[g1 g2 g3]) hline = lines; yline(i10+fd, LineStyle = '--', LineWidth = 2, Color = hline(1,:)) yline(i20+fd, LineStyle = '--', LineWidth = 2, Color = hline(2,:)) yline(i30+fd, LineStyle = '--', LineWidth = 2, Color = hline(3,:)) title('Group Delay Responses') xlabel("Normalized Frequency (\times\pi rad/sample)") ylabel("Group Delay") grid legend('N = 8','N = 32','N = 64',... 'Nominal Group Delay (N = 8)',... 'Nominal Group Delay (N = 32)',... 'Nominal Group Delay (N = 64)',Location='southwest'); ylim([-60,40]);
Design a fractional delay FIR filter using the designFracDelayFIR function. Pass the delay and the combined bandwidth as input arguments to the function.
Set delay to 0.786 and the target combined bandwidth to be 0.8. The function designs a filter that has a length of 22 taps, an integer latency i0 of 10 samples, and a combined bandwidth mbw of 0.8044 in normalized frequency units. This mbw value results in a combined bandwidth coverage of 80.44% of the frequency domain and exceeds the specified target combined bandwidth. The nominal group delay of the filter i0+fd equals 10.786.
fd = 0.786; tbw = 0.8; [h,i0,mbw] = designFracDelayFIR(FractionalDelay=fd,Bandwidth=tbw)
h = 1×22
0.0003 -0.0011 0.0026 -0.0052 0.0094 -0.0156 0.0248 -0.0386 0.0611 -0.1052 0.2512 0.9225 -0.1548 0.0769 -0.0455 0.0281 -0.0173 0.0102 -0.0057 0.0028 -0.0012 0.0003
i0 = 10
mbw = 0.8044
Plot the impulse response of the FIR.
stem((0:length(h)-1),h); xlabel('h'); ylabel('h[n]'); title('Impulse Response of the Fractional Delay FIR')
![Figure contains an axes object. The axes object with title Impulse Response of the Fractional Delay FIR, xlabel h, ylabel h[n] contains an object of type stem.](../../examples/dsp/win64/DesignAFracDelayFIRFiltWithSpecifiedDelayAndCombinedBWExample_01.png)
Plot the resulting magnitude response and the group delay response. Mark the nominal group delay and the combined bandwidth of the filter.
[H1,w] = freqz(h,1); G1 = grpdelay(h,1); figure; yyaxis left plot(w/pi,mag2db(abs(H1))) ylabel("Magnitude (dB)") hold on yyaxis right plot(w/pi,G1) ylabel("Group Delay (in samples)") hline = lines; xline(mbw, LineStyle =':', Color = 'b', LineWidth = 2) xline(tbw, LineStyle = '--', Color = 'm', LineWidth = 2) yline(i0+fd, LineStyle = ':', Color = 'r', LineWidth = 1) yticks([i0, i0+fd,i0+1:i0+9]); hold off title('Magnitude Responses (dB) and Group Delay', FontSize = 10) xlabel("Normalized Frequency (\times\pi rad/sample)") legend('Gain Response','Group Delay Response','Measured Combined Bandwidth',... 'Target Combined Bandwidth','Nominal Group Delay', ... Location = 'west', FontSize = 10)

Design a fractional delay FIR filter using the designFracDelayFIR function. Determine the group delay of the designed filter. Create a dsp.FIRFilter object that uses these designed coefficients and hence has the same group delay. Alternately, create a sampled sequence of a known function. Pass the sampled sequence to the FIR filter. Compare the output of the FIR filter to the shifted samples of the known function. Specify this shift to be equal to the group delay of the FIR filter. Verify that the two sequences match.
Set the delay of the FIR filter to 1/3 and the length to 6 taps.
fd = 1/3; len = 6;
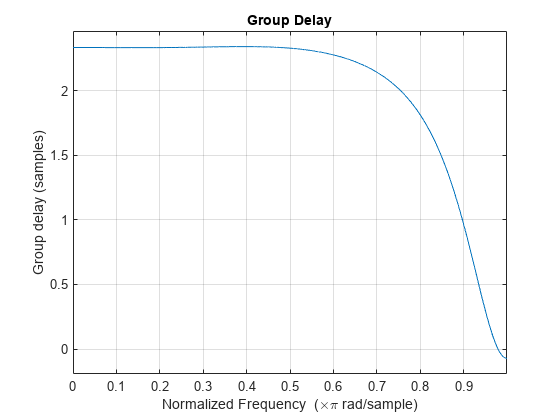
Design the filter using the designFracDelayFIR function and determine the center index i0 and the combined bandwidth bw of the filter. The group delay of this filter is i0 + fd or approximately 2.33 for the bandwidth of bw. To design the filter in single-precision, use the Datatype or like argument. Alternatively, you can specify any of the numerical arguments in single-precision.
[h,i0,bw] = designFracDelayFIR(FractionalDelay=fd,... FilterLength=len,Datatype="single")
h = 1×6 single row vector
0.0293 -0.1360 0.7932 0.3966 -0.1088 0.0257
i0 = single
2
bw = single
0.5158
Create a dsp.FIRFilter object and set its numerator to the filter coefficients h. This filter is now effectively a fractional delay FIR filter. Verify that the group delay response of this filter is approximately 2.33 for the duration of the bandwidth bw.
fdf = dsp.FIRFilter(h); grpdelay(fdf)
Compare with Shifted Function
Define a sequence x as samples of a known function.
f = @(t) (0.1*t.^2+cos(0.9*t)).*exp(-0.1*(t-5).^2);
n = (0:19)'; t = linspace(0,19,512);
x = f(n); % SamplesPlot the sampled values x against the original known function f(t).
scatter(n,x,20,'k','filled'); hold on; plot(t,f(t),'color',[0.5 0.5 0.5],'LineWidth',0.5) hold off; xlabel('Time') legend(["Input Samples","f(t)"]) title('Input Sequence with Known Underlying Analog Signal') ax = gca; ax.XGrid='on';

Pass the sampled sequence x through the FIR filter. Plot the input sequence and output sequence.
y = fdf(x); subplot(2,1,1); stem(x); title('Input Sequence'); xlabel('n') subplot(2,1,2) stem(y); title('FIR Output Sequence'); xlabel('n')

Shift the input sequence horizontally by i0 + fd, which is equal to the group delay of the FIR filter. Plot the function f(t-i0-FD). Verify that the input and output sequences fall roughly on the shifted function.
figure scatter(n,y,20,'red','filled') hold on; scatter(n+i0+fd,x,20,'black','filled') plot(t,f(t-i0-fd),'Color',[1,0.5,0.5],'LineWidth',0.1) xlabel('Time') legend(["Filter output","Shifted Input Samples","Shifted f(t-i0-fd)"]) hold off grid on title('Input and Output Sequences Aligned and Overlaid')

Name-Value Arguments
Specify optional pairs of arguments as
Name1=Value1,...,NameN=ValueN, where Name is
the argument name and Value is the corresponding value.
Name-value arguments must appear after other arguments, but the order of the
pairs does not matter.
Example: designFracDelayFIR(FractionalDelay=0.4,Bandwidth=0.8,SystemObject=true)
designs and returns a dsp.FIRFilter object.
Fractional delay of the filter, specified as a positive scalar in the range [0,1].
The fractional delay value that you specify determines the measured combined bandwidth
MBW of the filter.
When you set FractionalDelay to 0 or
1, the designed filter has a full bandwidth.
Data Types: single | double
Length of the fractional delay FIR filter, specified as an integer greater than 1.
Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64
Target combined bandwidth, specified as a positive scalar less than 0.999. This is the value of the combined bandwidth that the function must satisfy. Combined bandwidth is defined as the minimum of the gain bandwidth and the group delay bandwidth.
Specifying both filter length and target combined bandwidth results in an overdetermined design. The function does not support specifying both the values. When you specify the target combined bandwidth, the function determines the corresponding filter length, and designs the filter accordingly.
Specify a higher target combined bandwidth for a longer filter. For example,
setting Bandwidth to 0.9 yields a filter of length of 52, while
increasing Bandwidth to 0.99 yields a length of 724, which is
more than 10 times longer. As Bandwidth tends towards 1, the
filter length theoretically tends towards infinity.
Data Types: single | double
Since R2024b
Data type of the filter coefficients by type name, specified as
"double" or
"single".
You can use the Dataype or the
like argument to specify the
data type of the filter coefficients, but you cannot use both
arguments at the same time.
If you specify the data type of the filter coefficients using this argument, the function ignores the data types of the other numeric arguments.
Data Types: char | string
Since R2024b
Data type of the filter coefficients, specified as a prototype of a real floating-point value.
You can use the Dataype or the like
argument to specify the data type of filter coefficients, but you cannot use both
arguments at the same time.
If you specify the data type of the filter coefficients using this argument, the function ignores the data types of the other numeric arguments.
Example: B =
designFracDelayFIR(FractionalDelay=fd,FilterLength=filtLen,like=single(filtLen))
Example: filtLen = single(64); B =
designFracDelayFIR(FractionalDelay=fd,FilterLength=filtLen,like=filtLen)
Data Types: single | double
Since R2024a
Option to create a filter System object, specified as one of these:
false–– The function returns a vector of fractional delay FIR filter coefficients.true–– The function returns adsp.FIRFilterSystem object.
Data Types: logical
Option to print the entire function call in MATLAB, specified as one of these:
false–– The function does not print the function call.true–– The function prints the entire function call including the default values of theName=Valuearguments that you did not specify when calling the function.Use this argument to view all the values used by the function to design and implement the filter.
Data Types: logical
Output Arguments
Designed filter, returned as one of these options.
Fractional delay FIR filter coefficients –– The function returns a row vector of length N when you set the
SystemObjectargument tofalse.You can specify N through the
FilterLengthargument. If you specify theBandwidthargument, the function treats this value as the desired combined bandwidth, determines the corresponding filter length, and designs the filter accordingly.When you use filter length to design the filter, and you specify single-precision values in any of the input arguments, the function outputs single-precision filter coefficients. (since R2024a)
If you specify the data type using the
Datatypeor thelikeargument, the function ignores the data types of the other numeric arguments. (since R2024b)Multirate FIR filter object –– The function returns a
dsp.FIRFilterobject when you set theSystemObjectargument totrue.
Data Types: single | double
Integer latency of the designed FIR filter, returned as an integer value. Integer latency is the smallest integer shift required to make the symmetric Kaiser window causal. This value is approximately equal to half the filter length or N/2. For more details, see Integer latency, i0.
The nominal group delay of the filter is given by
i0+fd, where
fd is the value you specify through the
FractionalDelay argument.
If you specify the data type using the
Datatype or the like argument, the function
ignores the data types of the other numeric arguments. (since R2024b)
Data Types: single | double
Measured combined bandwidth, returned as a real positive scalar less than
0.999. This is the value of the combined bandwidth of the designed
filter. Combined bandwidth is defined as the minimum of gain bandwidth and
group delay
bandwidth.
The function designs the filter such that the measured combined bandwidth
MBW meets or exceeds the target combined bandwidth. The function
determines the filter length so that it meets the bandwidth constraint.
When you specify the filter length N, the function treats this
value as the desired length of the filter. The measured combined bandwidth in this case
varies with the length. Larger the value of N, higher is the measured
combined bandwidth MBW. This plot shows the variation. As the
filter length increases, the combined bandwidth of the filter moves closer towards 1.
The red dashed vertical line marks the combined bandwidth for each length. The
fractional delay value for each of these filters is 0.3

If you specify the data type using the
Datatype or the like argument, the function
ignores the data types of the other numeric arguments. (since R2024b)
Data Types: single | double
More About
The fractional delay FIR filter is an FIR approximation of an ideal sinc shift filter with a fractional (noninteger) delay value fd in the range [0,1].
The ideal shift filter models a band-limited D/A interpolator followed by shifted A/D uniform sampling. Assuming a uniform sampling rate and shift invariant interpolation, the resulting overall system can be expressed as a convolution filter, approximated by an FIR filter. In other words, , which encapsulates the D/A interpolation, shift, and A/D sampling chain as depicted in the figure.

where,
The frequency response of the ideal shift filter is
The ideal shift filter has a flat unity gain response, and a constant
group delay of fd, where fd is the fractional delay
value you specify through the FractionalDelay argument.
The function computes the FIR approximation by truncating the ideal filter and weighting the truncated filter by a Kaiser window.
where, is a Kaiser window of length N and has a shape parameter β. The function designs the Kaiser window to optimize the FIR frequency response, maximizing the combined bandwidths of both gain response and group delay response.
To make the FIR approximation causal, the algorithm introduces an additional shift of
i0, making the nominal group delay of the
filter equal to i0+fd. The
frequency response of the truncated filter is .
For more details, see Integer latency, i0.
Integer latency, i0, is the
smallest integer shift that is required to make the symmetric Kaiser window causal.
The ideal sinc shift filter is an allpass filter, which has an
infinite and noncausal impulse response. To approximate this filter, the function uses a
finite index Kaiser window of length N that is symmetric around the
origin and captures the main lobe of the sinc function.
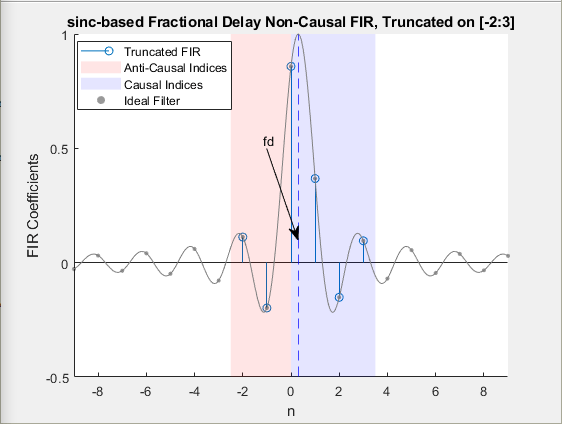
Due to the symmetric nature of the window, half of the window (approximately equal to
N/2) is on the negative side of the origin making the truncated filter
anti-causal. To make the truncated filter causal, shift the anti-causal (negative indices)
part of the FIR window by an integer latency,
i0, that is approximately equal to
N/2.

The overall delay of the causal FIR filter is
i0+fd, where
fd is the fractional delay.
For more details on FIR approximation, see the Causal FIR Approximations of an Ideal sinc Shift Filter section in Design Fractional Delay FIR Filters.
Given an FIR frequency response H(ω), the gain bandwidth is the largest interval [0 Ba] over which the gain response |H(ω)| is close to 1 up to a given tolerance value, tol.
Given tolerance tol and group delay response G, the group delay bandwidth is the largest interval [0 Bg] such that the group delay is close to the nominal value fd.
Combined bandwidth is defined as the minimum between gain bandwidth and group delay bandwidth.
Combined bandwidth depends on the fractional delay fd and the length of the FIR filter N.
Extended Capabilities
When you set the SystemObject argument to false,
the function supports code generation with no limitations.
When you set the SystemObject
argument to true, the inputs to the function must be constants when
generating code. (since R2024a)
This function supports strict single precision in
generated code. When you use filter length to design the filter, and you specify any of the
input arguments in single-precision, or use the
Datatype and like arguments to specify
single-precision (since R2024b), the code you generate uses strictly single-precision
arithmetic. (since R2024a)
Version History
Introduced in R2021aYou can now specify the data type of filter coefficients explicitly using the
Datatype and like arguments.
Starting in R2024a, specifying the arguments using the Value only
syntax is discouraged in the designFractionalDelayFIR function.
Existing instances of the function using the Value only arguments
continue to run but are discouraged. Instead, specify the arguments using the
Name=Value syntax.
Starting in R2024a, the designFractionalDelayFIR function supports
specifying the input arguments using the Name=Value syntax.
Here is the table that shows how to replace your existing code.
| Existing code | Replace with |
|---|---|
designFractionalDelayFIR(fd) | designFractionalDelayFIR(FractionalDelay=fd) |
N is an integer greater than 1. | designFractionalDelayFIR(FractionalDelay=fd,FilterLength=N) |
TBW is a positive scalar less than 0.999. | designFractionalDelayFIR(FractionalDelay=fd,Bandwidth=TBW) |
When you use filter length to design the filter, and you specify any of the input arguments in single-precision, the function designs filter coefficients in single precision both in simulation and in generated code.
You can now generate a dsp.FIRFilter object from the
designFracDelayFIR function by specifying the
'SystemObject' argument to true.
The designFractionalDelayFIR function supports code generation when
you set the 'SystemObject' flag to true.
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)