dsp.PhaseExtractor
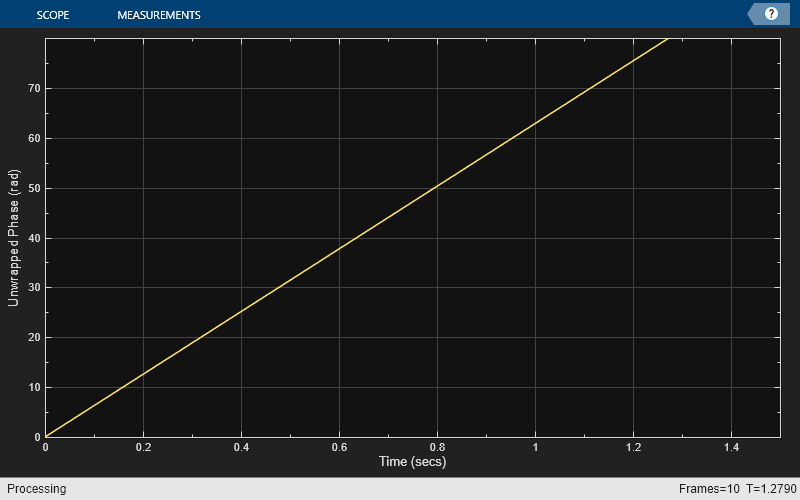
Extract the unwrapped phase of a complex input
Description
The dsp.PhaseExtractor
System object™ extracts the unwrapped phase of a real or a complex input.
To extract the unwrapped phase of a signal input:
Create the
dsp.PhaseExtractorobject and set its properties.Call the object with arguments, as if it were a function.
To learn more about how System objects work, see What Are System Objects?
Creation
Properties
Usage
Syntax
Description
Input Arguments
Output Arguments
Object Functions
To use an object function, specify the
System object as the first input argument. For
example, to release system resources of a System object named obj, use
this syntax:
release(obj)
Examples
Algorithms
Consider an input frame of length N:
The object acts on this frame and produces this output:
where:
Here, i runs from 1 to N. The angle function returns the phase angle in radians.
If the input signal consists of multiple frames:
If you set
TreatFramesIndependentlytotrue, the object treats each frame independently. Therefore, in each frame, the object calculates the phase using the preceding formula where:is 0.
is 1.
If you set
TreatFramesIndependentlytofalse, the object ignores boundaries between frames. Therefore, in each frame, thestepmethod calculates the phase using the preceding formula where:is the last unwrapped phase from the previous frame.
is the last sample from the previous frame.
Extended Capabilities
Version History
Introduced in R2014b