Main Content

Specify Gradient for HMC Sampler

Open Script

This example shows how to set up a Bayesian linear regression model for efficient posterior sampling using the Hamiltonian Monte Carlo (HMC) sampler. The prior distribution of the coefficients is a multivariate t, and the disturbance variance has an inverse gamma prior.

Consider the multiple linear regression model that predicts U.S. real gross national product (GNPR) using a linear combination of industrial production index (IPI), total employment (E), and real wages (WR).

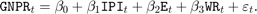
$$\texttt{GNPR}_t=\beta_0+\beta_1\texttt{IPI}_t+\beta_2\texttt{E}_t+\beta_3\texttt{WR}_t+\varepsilon_t.$$

For all 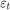$t$, $\varepsilon_t$ is a series of independent Gaussian disturbances with a mean of 0 and variance $\sigma^2$. Assume these prior distributions.

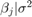  • $\beta_j\vert\sigma^2$ is a 4-D t distribution with 30 degrees of freedom for each component, correlation matrix C, location ct, and scale st.

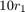  • $\sigma^2 \sim IG(10r_1,10r_2)$, with shape $10r_1$ and scale $10r_2$.

bayeslm treats these assumptions and the data likelihood as if the corresponding posterior is analytically intractable.

Declare a MATLAB® function that:

  • Accepts values of $\beta$ and $\sigma^2$ together in a column vector, and accepts values of the hyperparameters.

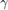  • Returns the log of the joint prior distribution, $\pi\left(\beta,\sigma^2\right)$, given the values of $\beta$ and $\sigma^2$, and returns the gradient of the log prior density with respect to $\beta$ and $\gamma$.

function [logPDF,gradient] = priorMVTIGHMC(params,ct,st,dof,C,a,b)
%priorMVTIGHMC Log density of multivariate t times inverse gamma and
%gradient
%   priorMVTIGHMC passes params(1:end-1) to the multivariate t density
%   function with dof degrees of freedom for each component and positive
%   definite correlation matrix C, and passes params(end) to the inverse
%   gamma distribution with shape a and scale b.  priorMVTIG returns the
%   log of the product of the two evaluated densities and its gradient.
%   After applying the log, terms involving constants only are dropped from
%   logPDF.
%   
%   params: Parameter values at which the densities are evaluated, an
%           m-by-1 numeric vector.
%
%       ct: Multivariate t distribution component centers, an (m-1)-by-1
%           numeric vector.  Elements correspond to the first m-1 elements
%           of params.
%
%       st: Multivariate t distribution component scales, an (m-1)-by-1
%           numeric vector.  Elements correspond to the first m-1 elements 
%           of params.
%
%      dof: Degrees of freedom for the multivariate t distribution, a
%           numeric scalar or (m-1)-by-1 numeric vector. priorMVTIG expands
%           scalars such that dof = dof*ones(m-1,1). Elements of dof
%           correspond to the elements of params(1:end-1).
%
%        C: correlation matrix for the multivariate t distribution, an
%           (m-1)-by-(m-1) symmetric, positive definite matrix. Rows and
%           columns correspond to the elements of params(1:end-1).
% 
%        a: Inverse gamma shape parameter, a positive numeric scalar.
%
%        b: Inverse gamma scale parameter, a positive scalar.
%
beta = params(1:(end-1));
numCoeffs = numel(beta);
sigma2 = params(end);

tVal = (beta - ct)./st;
expo = -(dof + numCoeffs)/2;
logmvtDensity = expo*log(1 + (1/dof)*((tVal'/C)*tVal));
logigDensity = (-a - 1)*log(sigma2) - 1/(sigma2*b);
logPDF = logmvtDensity + logigDensity;

grad_beta = (expo/(1 + (1/dof)*(tVal'/C*tVal)))*((2/dof)*((tVal'/C)'./st));
grad_sigma = (-a - 1)/sigma2 + 1/(sigma2^2*b);
gradient = [grad_beta; grad_sigma];
end

Create an anonymous function that operates like priorMVTIGHMC, but accepts the parameter values only and holds the hyperparameter values fixed at arbitrarily chosen values.

rng(1); % For reproducibility
dof = 30;
V = rand(4,4);
Sigma = V'*V;
st = sqrt(diag(Sigma));
C = Sigma./(st*st');
ct = -10*rand(4,1);
a = 10*rand;
b = 10*rand;
logPDF = @(params)priorMVTIGHMC(params,ct,st,dof,C,a,b);

Create a custom joint prior model for the linear regression parameters. Specify the number of predictors, p. Also, specify the function handle for priorMVTIGHMC and the variable names.

p = 3;
PriorMdl = bayeslm(p,'ModelType','custom','LogPDF',logPDF,...
    'VarNames',["IPI" "E" "WR"]);

PriorMdl is a customblm Bayesian linear regression model object representing the prior distribution of the regression coefficients and disturbance variance.

Load the Nelson-Plosser data set. Create variables for the response and predictor series. For numerical stability, convert the series to returns.

load Data_NelsonPlosser
X = price2ret(DataTable{:,PriorMdl.VarNames(2:end)});
y = price2ret(DataTable{:,'GNPR'});

Estimate the marginal posterior distributions of $\beta$ and $\sigma^2$ using the HMC sampler. To monitor the progress of the sampler, specify a verbosity level of 2. For numerical stability, specify reparameterization of the disturbance variance.

options = sampleroptions('Sampler','hmc','VerbosityLevel',2)
PosteriorMdl = estimate(PriorMdl,X,y,'Options',options,'Reparameterize',true);

options = 

  struct with fields:

                        Sampler: 'HMC'
           StepSizeTuningMethod: 'dual-averaging'
         MassVectorTuningMethod: 'iterative-sampling'
    NumStepSizeTuningIterations: 100
          TargetAcceptanceRatio: 0.6500
                  NumStepsLimit: 2000
                 VerbosityLevel: 2
                       NumPrint: 100

o Tuning mass vector using method: iterative-sampling 

o Initial step size for dual-averaging = 0.0625

|==================================================================================|
|   ITER   |    LOG PDF    |  STEP SIZE  |  NUM STEPS  |  ACC RATIO  |  DIVERGENT  |
|==================================================================================|
|      100 |  4.312313e+01 |   1.048e-01 |          48 |   6.300e-01 |           3 |
Finished mass vector tuning iteration 1 of 5. 

o Initial step size for dual-averaging = 0.5

|==================================================================================|
|   ITER   |    LOG PDF    |  STEP SIZE  |  NUM STEPS  |  ACC RATIO  |  DIVERGENT  |
|==================================================================================|
|      100 |  4.278350e+01 |   5.691e-01 |           9 |   6.300e-01 |           0 |

|==================================================================================|
|   ITER   |    LOG PDF    |  STEP SIZE  |  NUM STEPS  |  ACC RATIO  |  DIVERGENT  |
|==================================================================================|
|      100 |  4.080779e+01 |   4.112e-02 |           5 |   8.000e-01 |           0 |
Finished mass vector tuning iteration 2 of 5. 

o Initial step size for dual-averaging = 2

|==================================================================================|
|   ITER   |    LOG PDF    |  STEP SIZE  |  NUM STEPS  |  ACC RATIO  |  DIVERGENT  |
|==================================================================================|
|      100 |  4.044744e+01 |   3.088e-01 |          16 |   5.800e-01 |           0 |

|==================================================================================|
|   ITER   |    LOG PDF    |  STEP SIZE  |  NUM STEPS  |  ACC RATIO  |  DIVERGENT  |
|==================================================================================|
|      100 |  3.823729e+01 |   2.779e-01 |           4 |   7.700e-01 |           0 |
|      200 |  4.085115e+01 |   1.140e-01 |          15 |   8.433e-01 |           0 |
Finished mass vector tuning iteration 3 of 5. 

o Initial step size for dual-averaging = 0.25

|==================================================================================|
|   ITER   |    LOG PDF    |  STEP SIZE  |  NUM STEPS  |  ACC RATIO  |  DIVERGENT  |
|==================================================================================|
|      100 |  4.132405e+01 |   3.157e-01 |          16 |   6.500e-01 |           0 |

|==================================================================================|
|   ITER   |    LOG PDF    |  STEP SIZE  |  NUM STEPS  |  ACC RATIO  |  DIVERGENT  |
|==================================================================================|
|      100 |  4.357148e+01 |   1.591e-02 |           2 |   8.050e-01 |           0 |
|      200 |  3.890737e+01 |   2.841e-01 |          16 |   8.533e-01 |           0 |
Finished mass vector tuning iteration 4 of 5. 

o Initial step size for dual-averaging = 0.25

|==================================================================================|
|   ITER   |    LOG PDF    |  STEP SIZE  |  NUM STEPS  |  ACC RATIO  |  DIVERGENT  |
|==================================================================================|
|      100 |  4.358423e+01 |   3.442e-01 |          15 |   6.700e-01 |           0 |

|==================================================================================|
|   ITER   |    LOG PDF    |  STEP SIZE  |  NUM STEPS  |  ACC RATIO  |  DIVERGENT  |
|==================================================================================|
|      100 |  4.048687e+01 |   9.933e-02 |           4 |   7.950e-01 |           0 |
|      200 |  4.334420e+01 |   3.098e-01 |           4 |   8.433e-01 |           0 |
Finished mass vector tuning iteration 5 of 5. 

o Tuning step size using method: dual-averaging. Target acceptance ratio = 0.65

o Initial step size for dual-averaging = 0.5

|==================================================================================|
|   ITER   |    LOG PDF    |  STEP SIZE  |  NUM STEPS  |  ACC RATIO  |  DIVERGENT  |
|==================================================================================|
|      100 |  4.302411e+01 |   2.995e-01 |          17 |   6.100e-01 |           0 |

Method: MCMC sampling with 10000 draws
Number of observations: 61
Number of predictors:   4
 
           |   Mean     Std         CI95        Positive  Distribution 
-----------------------------------------------------------------------
 Intercept |  0.0077  0.0086  [-0.009,  0.024]    0.812     Empirical  
 IPI       | -0.1632  0.1461  [-0.476,  0.099]    0.123     Empirical  
 E         |  2.3694  0.5464  [ 1.396,  3.564]    1.000     Empirical  
 WR        | -0.2309  0.3023  [-0.844,  0.338]    0.219     Empirical  
 Sigma2    |  0.0036  0.0007  [ 0.002,  0.005]    1.000     Empirical

PosteriorMdl is an empiricalblm model object storing the draws from the posterior distributions.

View trace plots and autocorrelation function (ACF) plots of the draws from the posteriors.

for j = 1:4
    figure;
    subplot(2,1,1)
    plot(PosteriorMdl.BetaDraws(j,:));
    title(sprintf('Trace plot - Beta %d',j));
    xlabel('MCMC draw')
    ylabel('Simulation index')
    subplot(2,1,2)
    autocorr(PosteriorMdl.BetaDraws(j,:))
end

figure;
subplot(2,1,1)
plot(PosteriorMdl.Sigma2Draws);
title('Trace plot - Disturbance Variance');
xlabel('MCMC draw')
ylabel('Simulation index')
subplot(2,1,2)
autocorr(PosteriorMdl.Sigma2Draws)

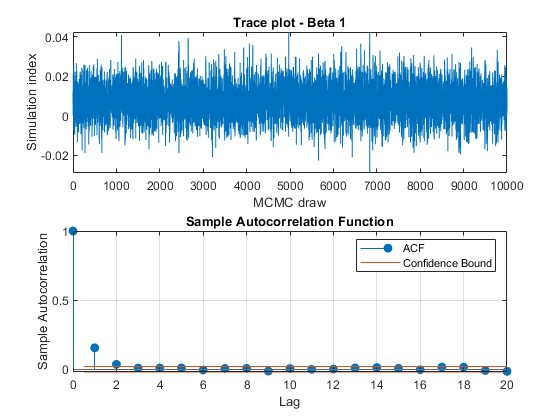
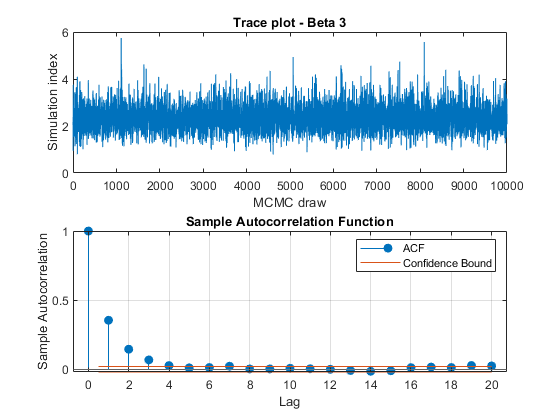
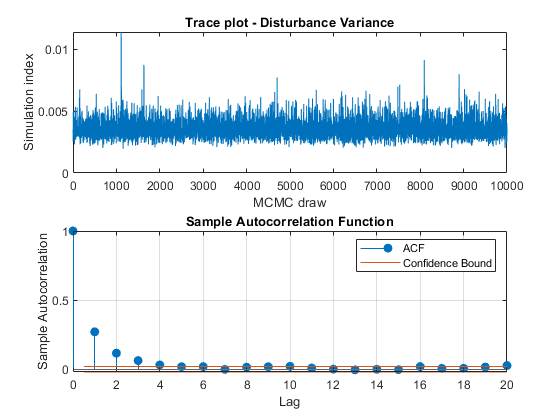
The trace plots show adequate mixing and no transient behavior. The autocorrelation plots show low correlation among subsequent samples.

See Also

Objects

Functions

Related Topics