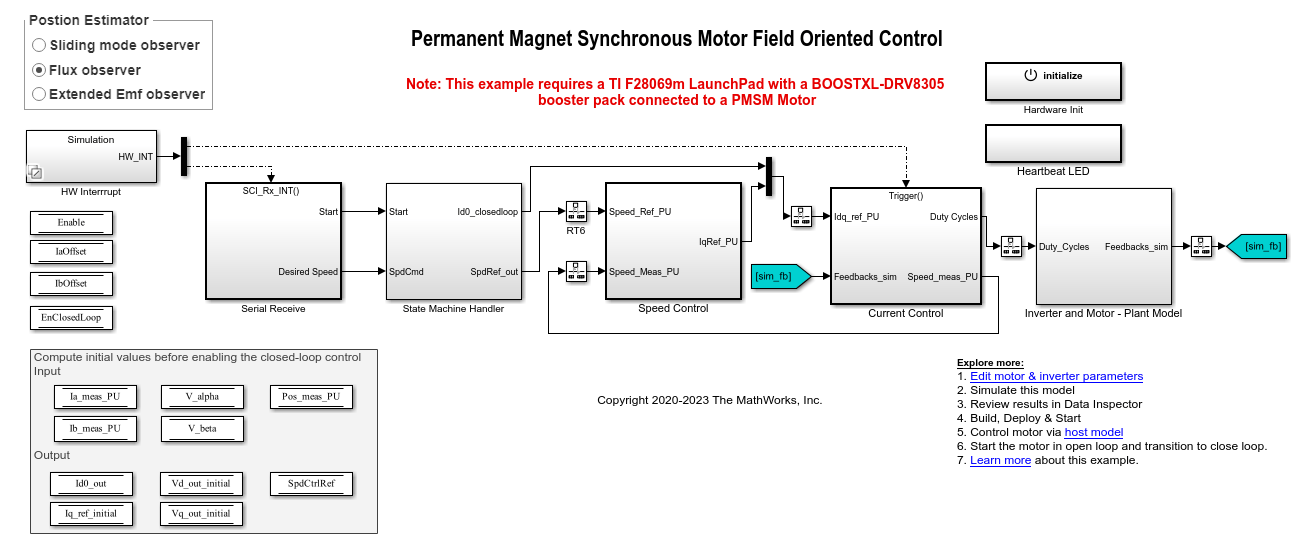
Flux Observer

Compute electrical position, magnetic flux, and electrical torque of rotor

Since R2020a

• 

Libraries:
Motor Control Blockset HDL Support / Sensorless Estimators
Motor Control Blockset / Sensorless Estimators

Description

The Flux Observer block computes the electrical position, magnetic flux, and electrical torque of a surface-mount permanent magnet synchronous motor (SPMSM) or an induction motor by using the per unit voltage and current values along the α- and β-axes in the stationary αβ reference frame.

The block also accepts 16-bit fixed-point data type inputs. To perform mathematical operations on 16-bit fixed-point data type signals, the block uses optimized implementation of equations for maintaining the best possible precision.

In addition, you can use the advanced options to enable the ParameterBus input port, which you can use with the Compute Parameter block to update the block parameters optimally at run-time. You can use this functionality when motor parameters can change over time, for example, while building applications that may require swapping of motors at run-time.

Equations

These equations describe how the block computes the electrical position, magnetic flux, and electrical torque for an SPMSM in the αβ reference frame.

$${\psi }_{\alpha }= {{\displaystyle \int }}^{\text{}}(V_{\alpha }-I_{\alpha }R)\text{dt}- \left(L_s\cdot I_{\alpha }\right)$$

${\psi }_{\beta }= {{\displaystyle \int }}^{\text{}}(V_{\beta }-I_{\beta }R)\text{dt}- \left(L_s\cdot I_{\beta }\right)$

If $$(V_{\alpha }-I_{\alpha }R)=v_1(t)$$ and $(V_{\beta }-I_{\beta }R)=v_2(t)$

Then, the following Laplace transforms represent the integral terms available in Ψ_α and Ψ_β:

$$\begin{array}{l}L\left({{\displaystyle \int }}^{\text{}}{\text{v}}_1\text{(t)dt}\right)=\frac{1}{s}L\left({\text{v}}_1\text{(t)}\right)=\frac{1}{s}{v}_1(s)\\ L\left({{\displaystyle \int }}^{\text{}}{\text{v}}_2\text{(t)dt}\right)=\frac{1}{s}L\left({\text{v}}_2\text{(t)}\right)=\frac{1}{s}{v}_2(s)\end{array}$$

The block uses low-pass filter (LPF) based integrator to compute these integral terms.

If the input electrical speed of the motor (ω_e) is much greater than the speed corresponding to the cutoff frequency of LPF-based integrator (ω_c), then

$$\begin{array}{l}L\left({{\displaystyle \int }}^{\text{}}{\text{v}}_1\text{(t)dt}\right)=\frac{1}{\left(s+{\omega }_c\right)}{v}_1(s)\\ L\left({{\displaystyle \int }}^{\text{}}{\text{v}}_2\text{(t)dt}\right)=\frac{1}{\left(s+{\omega }_c\right)}{v}_2(s)\end{array}$$

The LPF-based integrator does not allow any DC offset (in the block inputs) to ramp up the block output. For example, consider an input function X(s)=k/s corresponding to a step input x(t) = k*u(t). Using the preceding transfer function of the LPF-based integrator, $$G(s)=\frac{1}{\left(s+{\omega }_c\right)}$$, we obtain:

$$\begin{array}{l}Y(s)=G(s)X(s)=\frac{k}{s\left(s+{\omega }_c\right)}=\frac{k}{{\omega }_c}\left(\frac{1}{s}\right)-\frac{k}{{\omega }_c}\left(\frac{1}{s+{\omega }_c}\right)\\ Y(t)=\frac{k}{{\omega }_c}u(t)-\frac{k}{{\omega }_c}\exp \left(-{\omega }_{c}t\right)u(t)\end{array}$$

According to the preceding equation, the step response of the LPF integrator asymptotically settles to a DC value (that depends on the magnitude of the step input). Whereas the step response of a pure integrator is a ramp function. Using a highpass filter at the LPF integrator output eliminates the DC offset (present in the input) completely.

$$\psi = \sqrt{{\psi }_{\alpha }^2+{\psi }_{\beta }^2}$$

$T_{\text{e}}=\frac{3}{2}P({\psi }_{\alpha }{I}_{\beta }-{\psi }_{\beta }{I}_{\alpha })$

${\theta }_{\text{e}}= {\tan }^{-1}\frac{{\psi }_{\beta }}{{\psi }_{\alpha }}$

These equations describe how the block computes the rotor electrical position, rotor magnetic flux, and electrical torque for an induction motor.

$${\psi }_{\alpha }=\frac{L_r}{L_m} \left({{\displaystyle \int }}^{\text{}}(V_{\alpha }-I_{\alpha }R)\text{dt}- \sigma L_s{I}_{\alpha }\right)$$

$${\psi }_{\beta }=\frac{L_r}{L_m} \left({{\displaystyle \int }}^{\text{}}(V_{\beta }-I_{\beta }R)\text{dt}- \sigma L_s{I}_{\beta }\right)$$

$$\sigma =1-\frac{L_m^2}{L_r\cdot L_s}$$

$$\psi = \sqrt{{\psi }_{\alpha }^2+{\psi }_{\beta }^2}$$

$T_{\text{e}}=\frac{3}{2}\cdot P\cdot \frac{L_m}{L_r}({\psi }_{\alpha }{I}_{\beta }-{\psi }_{\beta }{I}_{\alpha })$

${\theta }_{\text{e}}= {\tan }^{-1}\frac{{\psi }_{\beta }}{{\psi }_{\alpha }}$

where:

• $V_{\alpha }$ and $V_{\beta }$ are the α-axis and β-axis voltages (volts).

• $I_{\alpha }$ and $I_{\beta }$ are the α-axis and β-axis current (amperes).

• $$R$$ is the stator resistance of the motor (ohms).

• $$L_s$$ is the stator inductance of the motor (henry).

• $$L_r$$ is the rotor inductance of the motor (henry).

• $$L_m$$ is the magnetizing inductance of the motor (henry).

• $\sigma$ is the total leakage factor of the induction motor.

• $$P$$ is the number of motor pole pairs.

• $$\psi$$ is the rotor magnetic flux (weber).

• ${\psi }_{\alpha }$ and ${\psi }_{\beta }$ are the rotor magnetic fluxes along the α- and β-axes (weber).

• $$T_e$$ is the electrical torque of the rotor (Nm).

• ${\theta }_e$ is the electrical position of the rotor (radians).

Examples

Sensorless Field-Oriented Control of PMSM

Implements the field-oriented control (FOC) technique to control the speed of a three-phase permanent magnet synchronous motor (PMSM). For details about FOC, see Field-Oriented Control (FOC).

Open Model

Sensorless Field-Oriented Control of Induction Motor

Uses sensorless position estimation to implement the field-oriented control (FOC) technique to control the speed of a three-phase AC induction motor (ACIM). For details about FOC, see Field-Oriented Control (FOC).

Open Model

Swap Motors with Single Deployment of Sensorless FOC Algorithm

Run a permanent magnet synchronous motor (PMSM) in an industrial drive application setup using a sensorless field-oriented control (FOC). The example uses a sensorless Flux Observer to estimate the motor position. Industrial drives enable you to replace a motor with a new one without repeated deployment of code. An industrial drive setup needs only nameplate parameters to adapt the software to the new motor.

Open Example

Ports

Input

V_α — α-axis voltage

scalar

Voltage component along the α-axis in the stationary αβ reference frame.

Data Types: single | double | fixed point

V_β — β-axis voltage

scalar

Voltage component along the β-axis in the stationary αβ reference frame.

Data Types: single | double | fixed point

I_α — α-axis current

scalar

Current along the α-axis in the stationary αβ reference frame.

Data Types: single | double | fixed point

I_β — β-axis current

scalar

Current along the β-axis in the stationary αβ reference frame.

Data Types: single | double | fixed point

Rst — Reset block

scalar

The pulse (true value) that resets the block algorithm.

Data Types: single | double | fixed point

ParameterBus — Computed parameters for flux observer

bus

Computed parameters for the Flux Observer block. You can specify the following parameters at this port:

• Pole pairs

• Stator resistance (ohm)

• Stator d-axis inductance (H)

• Stator leakage inductance (H)

• Rotor leakage inductance (H)

• Magnetizing inductance (H)

• Cutoff frequency (Hz)

Use this port along with the Compute Parameter block to update the preceding block parameters optimally at run-time.

Dependencies

To enable this port, select the Use input port for computed parameters (run-time motor swap) parameter available in the Advanced Options section.

Data Types: single | double

Output

θ_e — Electrical position of motor

scalar

The electrical position of the rotor as estimated by the block.

Dependencies

To enable this port, select the Position option in the Block output parameter.

Data Types: single | double | fixed point

Ψ — Rotor flux of motor

scalar

The magnetic flux of the rotor as estimated by the block.

Dependencies

To enable this port, select the Flux option in the Block output parameter.

Data Types: single | double | fixed point

T_e — Electrical torque of motor

scalar

The electrical torque of the motor as estimated by the block.

Dependencies

To enable this port, select the Torque option in the Block output parameter.

Data Types: single | double | fixed point

Parameters

Parameters

Motor selection — Type of motor

PMSM (default) | ACIM

Select the type of motor from the types that the block supports.

Support 16-bit fixedpoint datatype — Support the data type of 16-bit fixed-point

off (default) | on

To process 16-bit fixed-point inputs and perform computation using 16-bit fixed-point data type, select this parameter. To use a data type other than 16-bit fixed point, clear this parameter.

If you select this parameter:

• The block sets the Input unit parameter to Per-unit.

• The block selects the Position option in the Block output parameter because it does not support flux and torque computations when using the 16-bit data type.

Input unit — Unit of voltage and current inputs

SI unit (default) | Per-unit

Select the unit of the α- and β-axes voltage and current input values.

Base voltage (V) — Nominal voltage corresponding to one per-unit

13.86 (default) | scalar

The maximum phase voltage applied to the motor. For details, see Per-Unit System.

Dependencies

To enable this parameter, set Input unit to Per-unit.

Base current (A) — Nominal current corresponding to one per-unit

19.3 (default) | scalar

The maximum measurable current supplied to the motor. For details, see Per-Unit System.

Dependencies

To enable this parameter, set Input unit to Per-unit.

Block output — Block output options

Position | Flux | Torque

Select one or more quantities that you want the block to compute and display in the block output.

Note

You must select at least one value. The block displays an error message if you click Ok or Apply without selecting a value.

Pole pairs — Number of pole pairs available in motor

4 (default) | scalar

Number of pole pairs available in the motor.

Dependencies

To enable this parameter:

• Select the Torque option in the Block output parameter.

• Clear the Use input port for computed parameters (run-time motor swap) parameter available in the Advanced Options section.

Stator resistance (ohm) — Stator winding resistance

0.36 (default) | scalar

Stator phase winding resistance of the motor in ohms.

Dependencies

To enable this parameter, clear the Use input port for computed parameters (run-time motor swap) parameter available in the Advanced Options section.

Stator d-axis inductance (H) — Stator winding inductance along d-axis

0.2e-3 (default) | scalar

Stator winding inductance of the motor along the d-axis in henries.

Dependencies

To enable this parameter:

• Set Motor selection to PMSM.

• Clear the Use input port for computed parameters (run-time motor swap) parameter available in the Advanced Options section.

Stator leakage inductance (H) — Leakage inductance of stator winding

0.0068 (default) | scalar

Leakage inductance of the induction motor stator winding in henries.

Dependencies

To enable this parameter:

• Set Motor selection to ACIM.

• Clear the Use input port for computed parameters (run-time motor swap) parameter available in the Advanced Options section.

Rotor leakage inductance (H) — Leakage inductance of rotor winding

0.0068 (default) | scalar

Leakage inductance of the induction motor rotor winding in henries.

Dependencies

To enable this parameter:

• Set Motor selection to ACIM.

• Clear the Use input port for computed parameters (run-time motor swap) parameter available in the Advanced Options section.

Magnetizing inductance (H) — Magnetizing inductance of induction motor

0.0300 (default) | scalar

Magnetizing inductance of the induction motor in henries.

Dependencies

To enable this parameter:

• Set Motor selection to ACIM.

• Clear the Use input port for computed parameters (run-time motor swap) parameter available in the Advanced Options section.

Cutoff frequency (Hz) — Cutoff frequency of internal highpass filter

3.1863 (default) | scalar

Cutoff frequency of the internal highpass filter (that filters noise) in hertz.

The Flux Observer block uses an internal first-order IIR highpass filter. Set the Cutoff frequency (Hz) for this filter to a value that is lower than the electrical frequency corresponding to the minimum speed of the motor. For example, you can enter a value that is one-tenth of the minimum frequency of the motor currents. However, you can adjust this value to determine a more accurate cutoff frequency that generates the desired block output.

Dependencies

To enable this parameter, clear the Use input port for computed parameters (run-time motor swap) parameter available in the Advanced Options section.

Discrete step size (s) — Interval between consecutive block executions

50e-6 (default) | scalar

The fixed time interval in seconds between two consecutive instances of block execution.

Advanced Options

<argumentlist xml:id="mw_84ef2c43-db0f-460e-ad4c-833f72f50594">

Use input port for computed parameters (run-time motor swap) — Option to enable input port to accept computed parameters

off (default) | on

Select this parameter to enable the ParameterBus input port and disable the following parameters:

• Pole pairs

• Stator resistance (ohm)

• Stator d-axis inductance (H)

• Stator leakage inductance (H)

• Rotor leakage inductance (H)

• Magnetizing inductance (H)

• Cutoff frequency (Hz)

This parameter enables you to use the input port along with the Compute Parameter block to update block parameters optimally at run-time.

</argumentlist>

Datatypes

Position unit — Unit of electrical position output

Radians (default) | Degrees | Per-unit

Unit of the electrical position output.

Dependencies

To enable this parameter, select the Position option in the Block output parameter.

Position datatype — Data type of electrical position output

single (default) | double | fixed point

Data type of the electrical position output.

Dependencies

To enable this parameter, select the Position option in the Block output parameter.

Flux unit — Unit of magnetic flux output

Weber (default) | Per-unit

Unit of the magnetic flux output.

Dependencies

To enable this parameter, select the Flux option in the Block output parameter.

Per unit flux (Wb) — Flux corresponding to one per-unit

0.1 (default) | scalar

Flux value (in weber) corresponding to one per-unit. For details about the per-unit system, see Per-Unit System.

Dependencies

To enable this parameter:

• Select the Flux option in the Block output parameter.

• Set the Flux unit parameter to Per-unit.

Flux datatype — Data type of magnetic flux output

single (default) | double | fixed point

Data type of the magnetic flux output.

Dependencies

To enable this parameter, select the Flux option in the Block output parameter.

Torque unit — Unit of electrical torque output

Nm (default) | Per-unit

Unit of the electrical torque output.

Dependencies

To enable this parameter, select the Torque option in the Block output parameter.

Per unit torque (Nm) — Torque corresponding to one per-unit

100 (default) | scalar

Torque value (in Nm) corresponding to one per-unit. For details about the per-unit system, see Per-Unit System.

Dependencies

To enable this parameter:

• Select the Torque option in the Block output parameter.

• Set the Torque unit parameter to Per-unit.

Torque datatype — Data type of electrical torque output

single (default) | double | fixed point

Data type of the electrical torque output.

Dependencies

To enable this parameter, select the Torque option in the Block output parameter.

References

[1] A. Podder and D. Pandit, "Study of Sensorless Field-Oriented Control of SPMSM Using Rotor Flux Observer & Disturbance Observer Based Discrete Sliding Mode Observer," 2021 IEEE 22nd Workshop on Control and Modelling of Power Electronics (COMPEL), 2021, pp. 1-8. (doi: 10.1109/COMPEL52922.2021.9645939)

[2] O. Sandre-Hernandez, J. J. Rangel-Magdaleno and R. Morales-Caporal, "Simulink-HDL cosimulation of direct torque control of a PM synchronous machine based FPGA," 2014 11th International Conference on Electrical Engineering, Computing Science and Automatic Control (CCE), Campeche, 2014, pp. 1-6. (doi: 10.1109/ICEEE.2014.6978298)

[3] Y. Inoue, S. Morimoto and M. Sanada, "Control method suitable for direct torque control based motor drive system satisfying voltage and current limitations," The 2010 International Power Electronics Conference - ECCE ASIA -, Sapporo, 2010, pp. 3000-3006. (doi: 10.1109/IPEC.2010.5543698)

Extended Capabilities

C/C++ Code Generation
Generate C and C++ code using Simulink® Coder™.

HDL Code Generation

Generate VHDL, Verilog and SystemVerilog code for FPGA and ASIC designs using HDL Coder™.

HDL Coder™ provides additional configuration options that affect HDL implementation and synthesized logic.

HDL Architecture

This block has one default HDL architecture.

HDL Block Properties

ConstrainedOutputPipeline	Number of registers to place at the outputs by moving existing delays within your design. Distributed pipelining does not redistribute these registers. The default is 0. For more details, see ConstrainedOutputPipeline (HDL Coder).
InputPipeline	Number of input pipeline stages to insert in the generated code. Distributed pipelining and constrained output pipelining can move these registers. The default is 0. For more details, see InputPipeline (HDL Coder).
OutputPipeline	Number of output pipeline stages to insert in the generated code. Distributed pipelining and constrained output pipelining can move these registers. The default is 0. For more details, see OutputPipeline (HDL Coder).
SharingFactor	Number of functionally equivalent resources to map to a single shared resource. The default is 0. See also Resource Sharing (HDL Coder).

Restrictions

• The block supports HDL code generation only when you set the Motor selection parameter to PMSM.

• The block does not support HDL code generation when:

  • Input or output signals have mixed datatypes.

  • The parameter Support 16-bit fixedpoint datatype is selected.

  • Input or output signals have fixed point datatype of size less than 16 bits.

• The block needs native floating point library to support fixed point datatype with HDL code generation.

• If you run third-party (3p) simulation, the block may show a minor mismatch (of the order 1e-7) in the simulation results because of an internal trigonometric function that uses the floating point datatype.

Fixed-Point Conversion
Design and simulate fixed-point systems using Fixed-Point Designer™.

Version History

Introduced in R2020a