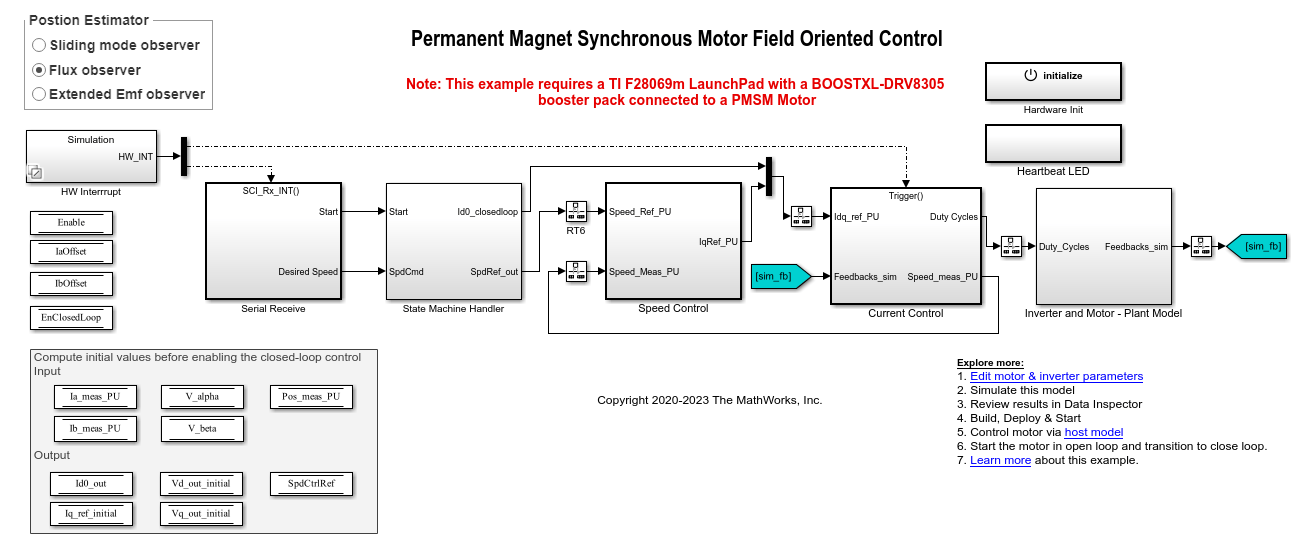
Sliding Mode Observer
Compute electrical position and mechanical speed of a surface-mount PMSM
Since R2021b
Libraries:
Motor Control Blockset /
Sensorless Estimators
Description
The Sliding Mode Observer block computes the electrical position and mechanical speed of a Surface Mount PMSM by using the voltage and current values along the α- and β-axes of the stationary αβ reference frame.
Equations
These equations describe the discrete-time operation of a PMSM:
These equations describe the discrete-time sliding mode observer operation of a surface mount PMSM:
If the back EMF observer fulfils the conditions and , there exists a k0, such that:
If the sliding mode observer fulfils these conditions:
then there exists a k=k0, such that for k≥k0:
where:
eα and iα are the stator back EMF and current for the α-axis.
eβ and iβ are the stator back EMF and current for the β-axis.
ẽα and ĩα are the errors in the stator back EMF and current for the α-axis.
ẽβ and ĩβ are the errors in the stator back EMF and current for the β-axis.
vα and vβ are the stator supply voltages.
R is the stator resistance.
L is the stator inductance.
g is the back EMF observer gain.
η is the current observer gain.
ωe is the electrical angular velocity.
Ts is the sampling period.
k is the sample count.
Tuning Sliding Mode Observer
Use these steps to tune the block using the Current observer gain (η) and Back-emf observer gain (g) parameters.
Select a back-emf observer gain (g) value such that . Bringing g close to the value
1, results in less error in the estimated back-emf. However, this makes convergence slow.Select a value of m based on the block sample time and maximum slope of the operating back-emf (such that ).
Select a current observer gain (η) value based on b, m, and g (such that ).
Note
The block functions correctly when you tune the sliding mode observer gains.
When using open-loop control to run a motor, compute the rotor position using both sliding mode observer and an actual sensor hardware and compare the computed position values. If the difference is acceptable, the block functions correctly. Otherwise, manually tune the sliding mode observer gains to ensure that the block functions accurately.
The transition from open-loop control to closed-loop control may fail due to noise in the currents and voltages. To make a successful transition, try reducing the value of the Filter cut-off frequency (Hz) parameter.
Examples
Ports
Input
Output
Parameters
References
[1] A. Podder and D. Pandit, "Study of Sensorless Field-Oriented Control of SPMSM Using Rotor Flux Observer & Disturbance Observer Based Discrete Sliding Mode Observer," 2021 IEEE 22nd Workshop on Control and Modelling of Power Electronics (COMPEL), 2021, pp. 1-8. (doi: 10.1109/COMPEL52922.2021.9645939)
[2] T. Bernardes, V. F. Montagner, H. A. Gründling, and H. Pinheiro, "Discrete-Time Sliding Mode Observer for Sensorless Vector Control of Permanent Magnet Synchronous Machine," in IEEE Transactions on Industrial Electronics, vol. 61, no. 4, pp. 1679-1691, 2014
[3] B. Bose, Modern Power Electronics and AC Drives. Prentice Hall, 2001. ISBN-0-13-016743-6.
[4] J. Liu and X. Wan, "Advanced Sliding Mode Control for Mechanical Systems". Springer-Verlag Berlin Heidelberg, 2011.
Extended Capabilities
Version History
Introduced in R2021b