lyapunovExponent
Characterize the rate of separation of infinitesimally close trajectories
Syntax
Description
lyapExp = lyapunovExponent(X,fs)X using sampling frequency fs. Use
lyapunovExponent to characterize the rate of separation
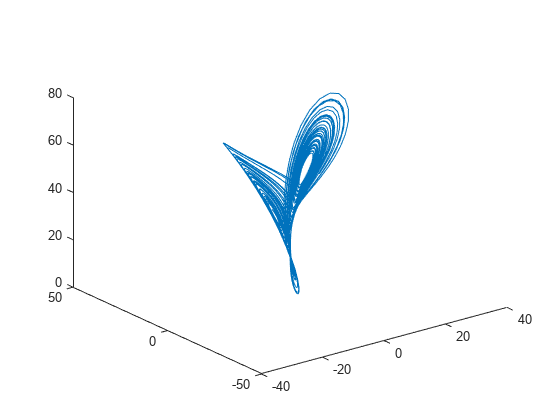
of infinitesimally close trajectories in phase space to distinguish different
attractors. Lyapunov exponent is useful in quantifying the level of chaos in a
system, which in turn can be used to detect potential faults.
___ = lyapunovExponent(___,
estimates the Lyapunov exponent with additional options specified by one or more
Name,Value)Name,Value pair arguments.
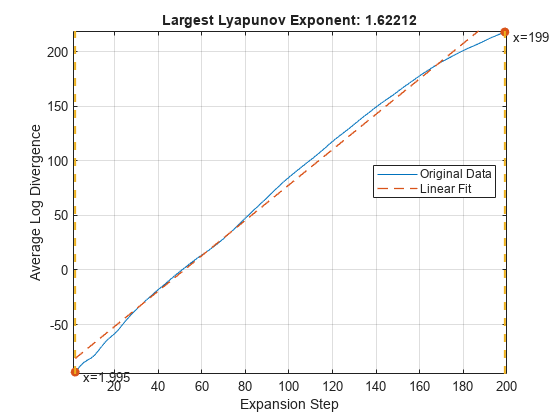
lyapunovExponent(___) with no output
arguments creates an average logarithmic divergence versus expansion step
plot.
Use the generated interactive plot to find an appropriate
ExpansionRange.
Examples
Input Arguments
Name-Value Arguments
Output Arguments
Algorithms
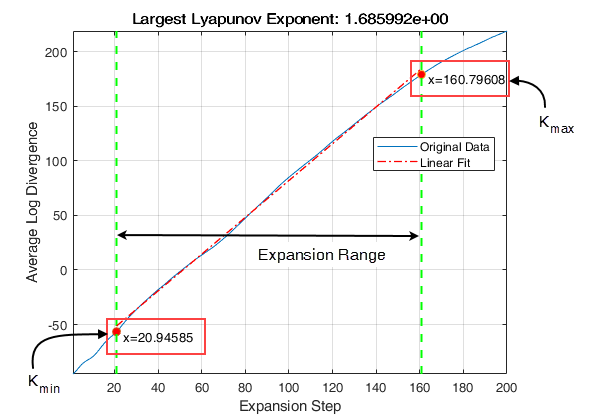
Lyapunov exponent is calculated in the following way:
The
lyapunovExponentfunction first generates a delayed reconstruction Y1:N with embedding dimension m, and lag τ.For a point
i, the software then finds the nearest neighbor point i* that satisfies such that , whereMinSeparation, the mean period, is the reciprocal of the mean frequency.From [1], the Lyapunov exponent for the entire expansion range is calculated as,
where, Kmin and Kmax represent
ExpansionRange,dtis the sampling time andA single value for the Lyapunov exponent is then calculated from the earlier step using the
polyfitcommand as,
References
[1] Michael T. Rosenstein , James J. Collins , Carlo J. De Luca. "A practical method for calculating largest Lyapunov exponents from small data sets ". Physica D 1993. Volume 65. Pages 117-134.
[2] Caesarendra, Wahyu & Kosasih, P & Tieu, Kiet & Moodie, Craig. "An application of nonlinear feature extraction-A case study for low speed slewing bearing condition monitoring and prognosis." IEEE/ASME International Conference on Advanced Intelligent Mechatronics: Mechatronics for Human Wellbeing, AIM 2013.1713-1718. 10.1109/AIM.2013.6584344.
[3] McCue, Leigh & W. Troesch, Armin. (2011). "Use of Lyapunov Exponents to Predict Chaotic Vessel Motions". Fluid Mechanics and its Applications. 97. 415-432. 10.1007/978-94-007-1482-3_23.
Extended Capabilities
Version History
Introduced in R2018a