dpss
Discrete prolate spheroidal (Slepian) sequences
Syntax
Description
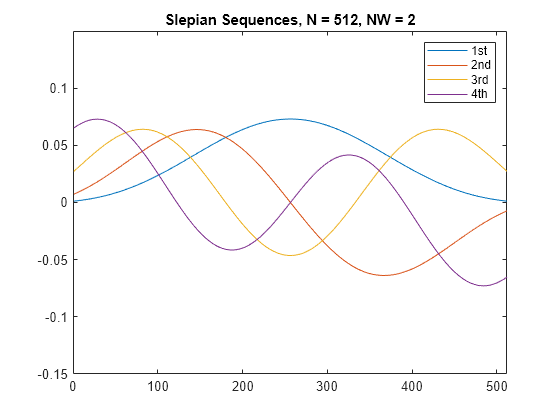
dpsSeq = dpss(seqLength,timeHalfBW)timeHalfBW) discrete prolate spheroidal (DPSS) or Slepian sequences of length
seqLength.
[
returns the frequency-domain energy concentration ratios dpsSeq,lambda] = dpss(seqLength,timeHalfBW)lambda
of the column vectors in dpsSeq. The ratios represent the
amount of energy in the passband [–W,W] to the
total energy from
[–Fs/2,Fs/2],
where Fs is the sample rate.
[___] = dpss(
returns the first seqLength,timeHalfBW,numSeq)numSeq Slepian sequences with a
time-half-bandwidth product equal to timeHalfBW. The function
returns the sequences in order of their energy concentration ratios.
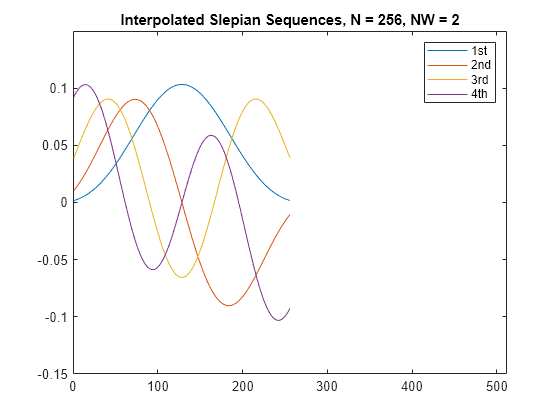
[___] = dpss(
uses interpolation to compute the DPSSs from a user-created database of DPSSs.
Create the database of DPSSs with seqLength,timeHalfBW,interpMethod)dpsssave and ensure that the resulting file,
dpss.mat, is in the MATLAB® search path.
[___] = dpss(___,
interpolates from DPSSs of length dpssLength)dpssLength in the database
dpss.mat.
[___] = dpss(___,"trace") prints the
method used to compute the DPSSs in the command window. Possible methods include
direct, spline interpolation, and linear interpolation.