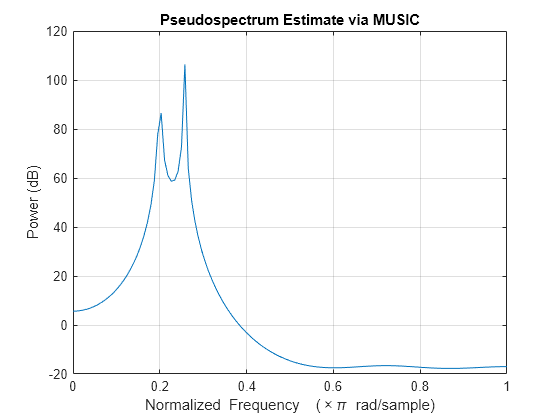
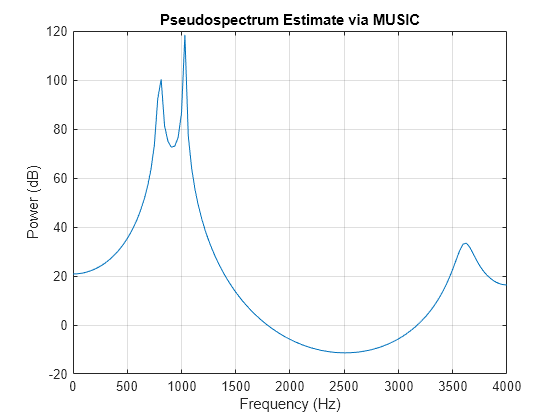
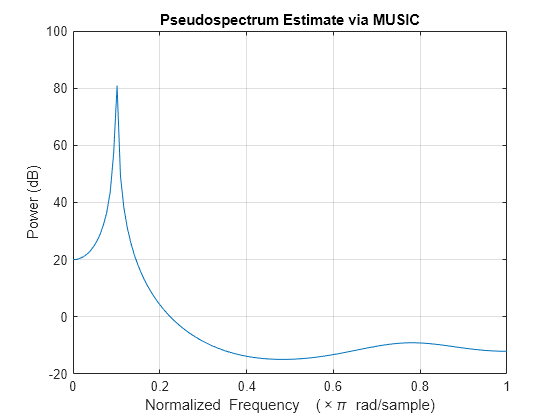
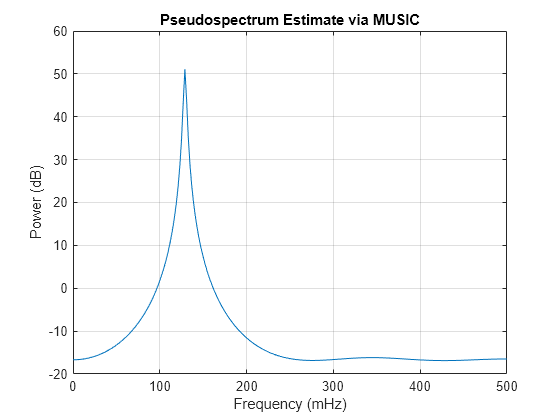
pmusic
Pseudospectrum using MUSIC algorithm
Syntax
Description
[
implements the multiple signal classification (MUSIC) algorithm and returns
S,wo] = pmusic(x,p)S, the pseudospectrum estimate of the input signal
x, and a vector wo of normalized frequencies
(in rad/sample) at which the pseudospectrum is evaluated. You can specify the signal
subspace dimension using the input argument p.
pmusic(___) with no output arguments plots the
pseudospectrum in the current figure window.
Examples
Input Arguments
Output Arguments
Tips
In the process of estimating the pseudospectrum, pmusic computes the
noise and signal subspaces from the estimated eigenvectors vj
and eigenvalues λj of the
signal's correlation matrix. The smallest of these eigenvalues is used in conjunction with the
threshold parameter p(2) to affect the dimension of the noise subspace in
some cases.
The length n of the eigenvectors computed by pmusic
is the sum of the dimensions of the signal and noise subspaces. This eigenvector length
depends on your input (signal data or correlation matrix) and the syntax you use.
The following table summarizes the dependency of the eigenvector length on the input argument.
Eigenvector Length Depending on Input Data and Syntax
Form of Input Data x | Comments on the Syntax | Length n of Eigenvectors |
|---|---|---|
Row or column vector |
|
|
Row or column vector |
|
|
Row or column vector |
| 2 × |
l-by-m matrix | If | m |
m-by-m nonnegative definite matrix |
| m |
You should specify nwin > p(1) or
length(nwin) > p(1) if you want
p(2) > 1 to have any effect.
Algorithms
The multiple signal classification (MUSIC) algorithm estimates the pseudospectrum from a signal or a correlation matrix using Schmidt's eigenspace analysis method [1]. The algorithm performs eigenspace analysis of the signal's correlation matrix to estimate the signal's frequency content. This algorithm is particularly suitable for signals that are the sum of sinusoids with additive white Gaussian noise. The eigenvalues and eigenvectors of the correlation matrix of the signal are estimated if you do not supply the correlation matrix.
The algorithm used to compute the MUSIC pseudospectrum estimate takes into account the relative sizes of the signal and noise subspaces.
If the dimension of the signal subspace is smaller than the dimension of the noise subspace, the MUSIC pseudospectrum estimate is given by
where p is the dimension of the signal subspace and vk is the kth eigenvector of the correlation matrix. The eigenvectors used in the sum correspond to the largest eigenvalues and span the signal subspace.
If the dimension of the noise subspace is smaller than the dimension of the signal subspace, the MUSIC pseudospectrum estimate is given by
where N is the dimension of the signal subspace plus the dimension of the noise subspace and vk is the kth eigenvector of the correlation matrix. The eigenvectors used in the sum correspond to the smallest eigenvalues and span the noise subspace.
In each case, the vector e(f) consists of complex exponentials, so the inner product vkHe(f) amounts to a Fourier transform. This is used for computation of the pseudospectrum estimate. The FFT is computed for each vk and then the squared magnitudes are summed.
References
[1] Marple, S. Lawrence. Digital Spectral Analysis. Englewood Cliffs, NJ: Prentice-Hall, 1987, pp. 373–378.
[2] Schmidt, R. O. “Multiple Emitter Location and Signal Parameter Estimation.” IEEE® Transactions on Antennas and Propagation. Vol. AP-34, March, 1986, pp. 276–280.
[3] Stoica, Petre, and Randolph L. Moses. Spectral Analysis of Signals. Upper Saddle River, NJ: Prentice Hall, 2005.
Extended Capabilities
Version History
Introduced before R2006a