Rotational Hard Stop
Double-sided rotational hard stop
Libraries:
Simscape /
Foundation Library /
Mechanical /
Rotational Elements
Description
The Rotational Hard Stop block represents a double-sided mechanical rotational hard stop that restricts the motion of a body between upper and lower bounds.
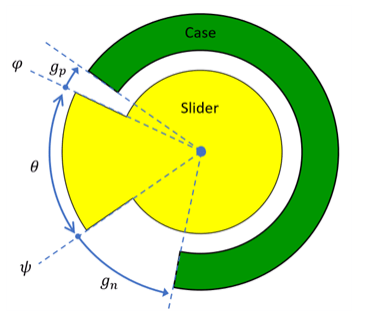
The slider connects to port R and the case connects to port C. The block transmits torque from port R to port C when the gap is closed in the positive direction.
The block computes the slider angular position, φ, from the slider angular velocity, ω = ωR - ωC.
θ is the slider arc angle and ψ is the slider angular position on the negative side, θ = |φ - ψ|. The block assumes the slider arc angle is 0 and does not model θ and ψ, but the schematic uses these symbols to explain the basic design of the hard stop.
gp is the initial gap on the positive side, measured from x:
For the positive gap to be open, gp must be positive.
A negative value of gp means that the slider is penetrating into the upper bound.
The gap is closed when gp - φ ≤ 0.
gn is the initial gap on the negative side, measured from y:
For the negative gap to be open, gn must be negative.
A positive value of gn means that the slider is penetrating into the lower bound.
The gap is closed when ψ - gn ≤ 0.
The block provides several modeling options:
Three options based on stiffness and damping. These models use similar underlying equations and differ in how stiffness and damping are applied at bounds.
A modeling option based on the coefficient of restitution. This model is different from the other three because it uses a mode chart to represent the hard stop behavior.
Models Based on Stiffness and Damping
In hard stop models based on stiffness and damping, the impact interaction between the slider and the stops is assumed to be elastic. This assumption means that the block represents the stop as a spring that comes into contact with the slider as the gap is cleared and opposes the slider penetration into the stop with a torque linearly proportional to this penetration. The block models this elasticity with the Contact stiffness at upper bound and Contact stiffness at lower bound parameters. To account for energy dissipation and nonelastic effects, the block uses the Contact damping at upper bound and Contact damping at lower bound parameters.
The basic hard stop model, Full stiffness and damping applied at
bounds, damped rebound, uses these equations:
where:
T is the interaction torque between the slider and the case.
gp is the initial gap between the slider and upper bound.
gn is the initial gap between the slider and lower bound.
φ is the slider angular position.
Kp is the contact stiffness at the upper bound.
Kn is the contact stiffness at the lower bound.
Dp is the damping coefficient at the upper bound.
Dn is the damping coefficient at the lower bound.
ω is the slider angular velocity.
t is time.
In the Full stiffness and damping applied at bounds, undamped
rebound hard stop model, the equations contain additional terms,
ge(ω,0) and
le(ω,0). These terms ensure that the
block does not apply damping on the rebound.
The relational functions ge (greater than or equal) and
le (less than or equal) do not generate zero crossings when
the angular velocity changes sign. For more information, see Enabling and Disabling Zero-Crossing Conditions in Simscape Language. However, the solver treats the
ge and le functions as nonlinear.
Therefore, if simscape.findNonlinearBlocks indicates that the
rest of your network is linear or switched linear, use the Full
stiffness and damping applied at bounds, damped rebound option to
improve performance.
The default hard stop model, Stiffness and damping applied smoothly
through transition region, damped rebound, adds two transitional
regions to the equations, one at each bound. When the slider travels through a
transition region, the block smoothly ramps up the torque from zero to the full
value. At the end of the transition region, the block applies the full stiffness and
damping. On the rebound, the block smoothly decreases both stiffness and damping
torques to zero. These equations also use the ge and
le relational functions, which do not produce zero
crossings.
Model Based on Coefficient of Restitution
Unlike the models based on stiffness and damping, this model does not allow penetration of slider into the hard stops. The hard stop behavior is represented by a mode chart with three regular modes and three instantaneous modes:
FREE— There is no torque transmission between the slider and case.CONTACT_UPPER— The positive gap is closed.CONTACT_LOWER— The negative gap is closed.RELEASE_UPPER— The instantaneous mode needed to transition fromCONTACT_UPPERtoFREE.RELEASE_LOWER— The instantaneous mode needed to transition fromCONTACT_LOWERtoFREE.IMPACT— The instantaneous mode used when the slider bounces.
When the slider hits the case slowly, with speed less than the static contact speed threshold, the slider and case stay in contact. Otherwise, the slider bounces. When the slider bounces, it loses the speed due to the coefficient of restitution. In either of the contact modes, slider speed ω = 0. To transition from a contact mode to free mode, a torque greater than the static contact release torque threshold must be applied to the slider, and the transition must go through an instantaneous release mode to set the initial speed.
This modeling option improves simulation performance because static contact mode does not require the block to keep computing hard stop torque when the block is in contact mode.
Variables
To set the priority and initial target values for the block variables prior to simulation, use the Initial Targets section in the block dialog box or Property Inspector. For more information, see Set Priority and Initial Target for Block Variables.
Nominal values provide a way to specify the expected magnitude of a variable in a model. Using system scaling based on nominal values increases the simulation robustness. Nominal values can come from different sources, one of which is the Nominal Values section in the block dialog box or Property Inspector. For more information, see Modify Nominal Values for a Block Variable.
