PartitionedDirectForecaster
Description
PartitionedDirectForecaster is a set of direct forecasting models
trained on partitioned, regularly sampled time series data. You can evaluate the quality of
the cross-validated direct forecasting model by using the cvloss and
cvpredict object
functions.
The cvloss and cvpredict object functions use
models trained on training observations to predict the response for test observations. For
example, suppose you cross-validate a direct forecasting model that predicts one step ahead by
using five sliding windows. In this case, the software splits the data set into five windows
with fixed-size training and test sets. Cross-validation proceeds as follows:
The software trains the first model (stored in
CVMdl.Learners{1}) by using the observations in the first training set, and uses the observations in the first test set for validation.The software trains the second model (stored in
CVMdl.Learners{2}) by using the observations in the second training set, and uses the observations in the second test set for validation.The software proceeds in a similar way for the third, fourth, and fifth models.
If you validate by using cvpredict, the software computes predictions
for the observations in test set i by using model i. If
an observation is in more than one test set, then the function returns the prediction for that
observation, averaged over all test sets, by default.
Creation
You can create a PartitionedDirectForecaster model in two ways:
Create a cross-validated model from a direct forecasting object
DirectForecasterby using thecrossvalobject function.Create a cross-validated model by using the
directforecasterfunction and specifying thePartitionname-value argument.
Properties
Partition and Learner Properties
This property is read-only.
Compact direct forecasting models used for cross-validation, specified as a cell
array of CompactDirectForecaster model objects. The number of models in
Learners matches the number of test sets in the data partition
Partition.
Data Types: cell
This property is read-only.
Template for the regression models in each Learners model,
specified as the output of one of these template functions.
| Template Function | Description |
|---|---|
templateEnsemble | Ensemble learning template, with the ensemble aggregation method specified as
"Bag" or "LSBoost" |
templateGAM | General additive model template |
templateGP | Gaussian process regression model template |
templateKernel | Kernel model template |
templateLinear | Linear learner template |
templateSVM | Support vector machine template |
templateTree | Decision tree template |
This property is read-only.
Data partition indicating how the software splits the data for cross-validation,
specified as a tspartition
object. The model uses expanding window cross-validation, sliding window
cross-validation, or holdout validation.
Data Properties
This property is read-only.
Indices of categorical exogenous predictors, specified as a positive integer
vector. Each index value in CategoricalPredictors indicates that
the corresponding exogenous predictor in X is categorical. (See
PredictorNames for the list of exogenous predictors.) If none
of the exogenous predictors are categorical, then this property is empty
([]).
Data Types: double
This property is read-only.
Number of observations in the data stored in X and
Y, specified as a positive integer scalar.
Data Types: double
This property is read-only.
Names of the exogenous predictors, specified as a cell array of character vectors.
The order of the elements in PredictorNames corresponds to the
order of the exogenous predictors in X.
Data Types: cell
This property is read-only.
Name of the response variable, specified as a character vector.
Data Types: char
This property is read-only.
Exogenous predictor data used to cross-validate the model, specified as a numeric
matrix, table, or timetable. Each row of X corresponds to one
observation, and each column corresponds to one variable.
This property is read-only.
Response data used to cross-validate the model, specified as a numeric vector,
one-column table, or one-column timetable. Each row of Y
corresponds to one observation.
Forecasting and Prepared Data Properties
This property is read-only.
Future time steps at which to forecast, specified as a positive integer vector.
Each of the compact direct forecasting models in Learners
contains a regression model for each horizon step.
For example, if the Horizon value of a cross-validated direct
forecasting model CVMdl is [1 3], then
CVMdl.Learners{1}.Learners contains two regression models: one
that forecasts at horizon step 1 and one that forecasts at horizon
step 3.
Data Types: double
This property is read-only.
Leading predictor lags used for preparing leading exogenous predictors, specified as a nonnegative integer vector or cell array of nonnegative integer vectors.
If
LeadingPredictorLagsis a vector, then for each elementiin the vector, the software shifts the leading exogenous predictors backward in time byisteps, relative to the horizon time step. The software uses the resulting features as predictors. When theLeadingPredictorLagsvalue is0, the software uses the unshifted leading predictors.For example, if the
Horizonvalue of a cross-validated direct forecasting modelCVMdlis3and theLeadingPredictorLagsvalue is0, then the software uses the unshifted leading predictor values at horizon step3as predictor values.If
LeadingPredictorLagsis a cell array, then the numeric values in elementiof the cell array indicate the lags for leading exogenous predictori.
If no leading predictor lags are used, then this property is empty
([]).
Data Types: double | cell
This property is read-only.
Indices of the leading exogenous predictors, specified as a positive integer
vector. Leading predictors are predictors for which future values are known. Each
index value in LeadingPredictors indicates that the corresponding
exogenous predictor in X is leading. (See
PredictorNames for the list of exogenous predictors.) If no
exogenous predictors are leading predictors, then this property is empty
([]).
Data Types: double
This property is read-only.
Maximum lag value, specified as a nonnegative integer scalar. The
MaxLag value depends on the values in
ResponseLags, PredictorLags, and
LeadingPredictorLags. Specifically, the software computes the
maximum lag as
follows:
MaxLag = max([0,ResponseLags,PredictorLags, ...
LeadingPredictorLags - min(Horizon) + 1])Data Types: double
This property is read-only.
Predictor lags used for preparing nonleading exogenous predictors, specified as a positive integer vector or cell array of positive integer vectors.
If
PredictorLagsis a vector, then for each elementiin the vector, the software shifts the nonleading exogenous predictors backward in time byisteps and uses the resulting features as predictors.If
PredictorLagsis a cell array, then the numeric values in elementiof the cell array indicate the lags for nonleading exogenous predictori.
If no predictor lags are used, then this property is empty
([]).
Data Types: double | cell
This property is read-only.
Indices of the prepared categorical predictors, specified as a positive integer
vector. Each index value in PreparedCategoricalPredictors
indicates that the corresponding predictor listed in
PreparedPredictorNames is categorical. If no prepared
predictors are categorical predictors, then this property is empty
([]).
Data Types: double
This property is read-only.
Names of the prepared predictors, specified as a cell array of character vectors.
These prepared predictors include variables created from both the predictor variables
in X and the response variable Y. Not every
predictor is used at every horizon step. To see which predictors are used at a
specific horizon step, consult the PreparedPredictorsPerHorizon
table.
Data Types: cell
This property is read-only.
Prepared predictors at each horizon step, specified as a table of logical values.
Each row of the table corresponds to a horizon step, and each column of the table
corresponds to a prepared predictor as listed in
PreparedPredictorNames. The logical value in row
i and column j indicates whether the software
uses prepared predictor j at horizon step i. If
the value is 1 (true), then the software uses
the predictor. If the value is 0 (false), then
the software does not use the predictor.
Data Types: table
This property is read-only.
Names of the prepared responses at each horizon step, specified as a cell array of
character vectors. That is, element i of
PreparedResponseNames is the name of the response variable at
horizon step i.
For example, given a cross-validated direct forecasting model
CVMdl, the name of the response variable at horizon step
1, CVMdl.PreparedResponseNames{1}, matches the
response variable name used in the first regression model of each compact direct
forecasting model in Learners (such as
CVMdl.Learners{1}.Learners{1}.ResponseName).
Data Types: cell
This property is read-only.
Response lags used for preparing predictors, specified as a positive integer
vector. Each element in ResponseLags indicates the number of time
steps by which to shift the response backward in time. The resulting feature is used
as a predictor. If no response lags are used, then this property is empty
([]).
Data Types: double
Object Functions
Examples
Create a cross-validated direct forecasting model using expanding window cross-validation. To evaluate the performance of the model:
Compute the mean squared error (MSE) on each test set using the
cvlossobject function.For each test set, compare the true response values to the predicted response values using the
cvpredictobject function.
Load the sample file TemperatureData.csv, which contains average daily temperature from January 2015 through July 2016. Read the file into a table. Observe the first eight observations in the table.
Tbl = readtable("TemperatureData.csv");
head(Tbl) Year Month Day TemperatureF
____ ___________ ___ ____________
2015 {'January'} 1 23
2015 {'January'} 2 31
2015 {'January'} 3 25
2015 {'January'} 4 39
2015 {'January'} 5 29
2015 {'January'} 6 12
2015 {'January'} 7 10
2015 {'January'} 8 4
Create a datetime variable t that contains the year, month, and day information for each observation in Tbl.
numericMonth = month(datetime(Tbl.Month, ... InputFormat="MMMM",Locale="en_US")); t = datetime(Tbl.Year,numericMonth,Tbl.Day);
Plot the temperature values in Tbl over time.
plot(t,Tbl.TemperatureF) xlabel("Date") ylabel("Temperature in Fahrenheit")
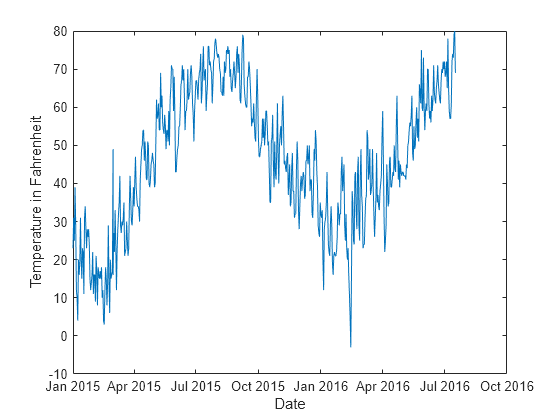
Create a direct forecasting model by using the data in Tbl. Train the model using a bagged ensemble of trees. All three of the predictors (Year, Month, and Day) are leading predictors because their future values are known. To create new predictors by shifting the leading predictor and response variables backward in time, specify the leading predictor lags and the response variable lags.
Mdl = directforecaster(Tbl,"TemperatureF", ... Learner="bag", ... LeadingPredictors="all",LeadingPredictorLags={0:1,0:1,0:7}, ... ResponseLags=1:7)
Mdl =
DirectForecaster
Horizon: 1
ResponseLags: [1 2 3 4 5 6 7]
LeadingPredictors: [1 2 3]
LeadingPredictorLags: {[0 1] [0 1] [0 1 2 3 4 5 6 7]}
ResponseName: 'TemperatureF'
PredictorNames: {'Year' 'Month' 'Day'}
CategoricalPredictors: 2
Learners: {[1×1 classreg.learning.regr.CompactRegressionEnsemble]}
MaxLag: 7
NumObservations: 565
Properties, Methods
Mdl is a DirectForecaster model object. By default, the horizon is one step ahead. That is, Mdl predicts a value that is one step into the future.
Partition the time series data in Tbl using an expanding window cross-validation scheme. Create three training sets and three test sets, where each test set has 100 observations. Note that each observation in Tbl is in at most one test set.
CVPartition = tspartition(size(Mdl.X,1),"ExpandingWindow",3, ... TestSize=100)
CVPartition =
tspartition
Type: 'expanding-window'
NumObservations: 565
NumTestSets: 3
TrainSize: [265 365 465]
TestSize: [100 100 100]
StepSize: 100
Properties, Methods
The training sets increase in size from 265 observations in the first window to 465 observations in the third window.
Create a cross-validated direct forecasting model using the partition specified in CVPartition. Inspect the Learners property of the resulting CVMdl object.
CVMdl = crossval(Mdl,CVPartition)
CVMdl =
PartitionedDirectForecaster
Partition: [1×1 tspartition]
Horizon: 1
ResponseLags: [1 2 3 4 5 6 7]
LeadingPredictors: [1 2 3]
LeadingPredictorLags: {[0 1] [0 1] [0 1 2 3 4 5 6 7]}
ResponseName: 'TemperatureF'
PredictorNames: {'Year' 'Month' 'Day'}
CategoricalPredictors: 2
Learners: {3×1 cell}
MaxLag: 7
NumObservations: 565
Properties, Methods
CVMdl.Learners
ans=3×1 cell array
{1×1 timeseries.forecaster.CompactDirectForecaster}
{1×1 timeseries.forecaster.CompactDirectForecaster}
{1×1 timeseries.forecaster.CompactDirectForecaster}
CVMdl is a PartitionedDirectForecaster model object. The crossval function trains CVMdl.Learners{1} using the observations in the first training set, CVMdl.Learner{2} using the observations in the second training set, and CVMdl.Learner{3} using the observations in the third training set.
Compute the average test set MSE.
averageMSE = cvloss(CVMdl)
averageMSE = 53.3480
To obtain more information, compute the MSE for each test set.
individualMSE = cvloss(CVMdl,Mode="individual")individualMSE = 3×1
44.1352
84.0695
31.8393
The models trained on the first and third training sets seem to perform better than the model trained on the second training set.
For each test set observation, predict the temperature value using the corresponding model in CVMdl.Learners.
predictedY = cvpredict(CVMdl); predictedY(260:end,:)
ans=306×1 table
TemperatureF_Step1
__________________
NaN
NaN
NaN
NaN
NaN
NaN
50.963
57.363
57.04
60.705
59.606
58.302
58.023
61.39
67.229
61.083
⋮
Only the last 300 observations appear in any test set. For observations that do not appear in a test set, the predicted response value is NaN.
For each test set, plot the true response values and the predicted response values.
tiledlayout(3,1) nexttile idx1 = test(CVPartition,1); plot(t(idx1),Tbl.TemperatureF(idx1)) hold on plot(t(idx1),predictedY.TemperatureF_Step1(idx1)) legend("True Response","Predicted Response", ... Location="eastoutside") xlabel("Date") ylabel("Temperature") title("Test Set 1") hold off nexttile idx2 = test(CVPartition,2); plot(t(idx2),Tbl.TemperatureF(idx2)) hold on plot(t(idx2),predictedY.TemperatureF_Step1(idx2)) legend("True Response","Predicted Response", ... Location="eastoutside") xlabel("Date") ylabel("Temperature") title("Test Set 2") hold off nexttile idx3 = test(CVPartition,3); plot(t(idx3),Tbl.TemperatureF(idx3)) hold on plot(t(idx3),predictedY.TemperatureF_Step1(idx3)) legend("True Response","Predicted Response", ... Location="eastoutside") xlabel("Date") ylabel("Temperature") title("Test Set 3") hold off
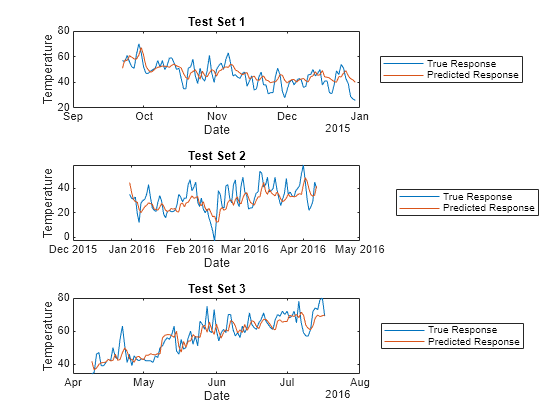
Overall, the cross-validated direct forecasting model is able to predict the trend in temperatures. If you are satisfied with the performance of the cross-validated model, you can use the full DirectForecaster model Mdl for forecasting at time steps beyond the available data.
Create a partitioned direct forecasting model using holdout validation. To evaluate the performance of the model:
At each horizon step, compute the root relative squared error (RRSE) on the test set using the
cvlossobject function.At each horizon step, compare the true response values to the predicted response values using the
cvpredictobject function.
Load the sample file TemperatureData.csv, which contains average daily temperature from January 2015 through July 2016. Read the file into a table. Observe the first eight observations in the table.
Tbl = readtable("TemperatureData.csv");
head(Tbl) Year Month Day TemperatureF
____ ___________ ___ ____________
2015 {'January'} 1 23
2015 {'January'} 2 31
2015 {'January'} 3 25
2015 {'January'} 4 39
2015 {'January'} 5 29
2015 {'January'} 6 12
2015 {'January'} 7 10
2015 {'January'} 8 4
Create a datetime variable t that contains the year, month, and day information for each observation in Tbl.
numericMonth = month(datetime(Tbl.Month, ... InputFormat="MMMM",Locale="en_US")); t = datetime(Tbl.Year,numericMonth,Tbl.Day);
Plot the temperature values in Tbl over time.
plot(t,Tbl.TemperatureF) xlabel("Date") ylabel("Temperature in Fahrenheit")
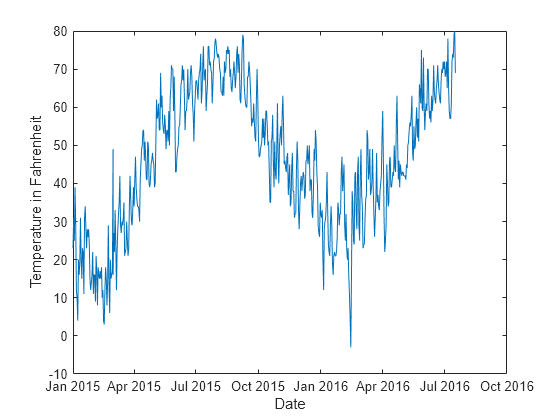
Create a direct forecasting model by using the data in Tbl. Specify the horizon steps as one, two, and three steps ahead. Train a model at each horizon using a bagged ensemble of trees. All three of the predictors (Year, Month, and Day) are leading predictors because their future values are known. To create new predictors by shifting the leading predictor and response variables backward in time, specify the leading predictor lags and the response variable lags.
rng("default") Mdl = directforecaster(Tbl,"TemperatureF", ... Horizon=1:3,Learner="bag", ... LeadingPredictors="all",LeadingPredictorLags={0:1,0:1,0:7}, ... ResponseLags=1:7)
Mdl =
DirectForecaster
Horizon: [1 2 3]
ResponseLags: [1 2 3 4 5 6 7]
LeadingPredictors: [1 2 3]
LeadingPredictorLags: {[0 1] [0 1] [0 1 2 3 4 5 6 7]}
ResponseName: 'TemperatureF'
PredictorNames: {'Year' 'Month' 'Day'}
CategoricalPredictors: 2
Learners: {3×1 cell}
MaxLag: 7
NumObservations: 565
Properties, Methods
Mdl is a DirectForecaster model object. Mdl consists of three regression models: Mdl.Learners{1}, which predicts one step ahead; Mdl.Learners{2}, which predicts two steps ahead; and Mdl.Learners{3}, which predicts three steps ahead.
Partition the time series data in Tbl using a holdout validation scheme. Reserve 20% of the observations for testing.
holdoutPartition = tspartition(size(Mdl.X,1),"Holdout",0.20)holdoutPartition =
tspartition
Type: 'holdout'
NumObservations: 565
NumTestSets: 1
TrainSize: 452
TestSize: 113
Properties, Methods
The test set consists of the latest 113 observations.
Create a partitioned direct forecasting model using the partition specified in holdoutPartition.
holdoutMdl = crossval(Mdl,holdoutPartition)
holdoutMdl =
PartitionedDirectForecaster
Partition: [1×1 tspartition]
Horizon: [1 2 3]
ResponseLags: [1 2 3 4 5 6 7]
LeadingPredictors: [1 2 3]
LeadingPredictorLags: {[0 1] [0 1] [0 1 2 3 4 5 6 7]}
ResponseName: 'TemperatureF'
PredictorNames: {'Year' 'Month' 'Day'}
CategoricalPredictors: 2
Learners: {[1×1 timeseries.forecaster.CompactDirectForecaster]}
MaxLag: 7
NumObservations: 565
Properties, Methods
holdoutMdl is a PartitionedDirectForecaster model object. Because holdoutMdl uses holdout validation rather than a cross-validation scheme, the Learners property of the object contains one CompactDirectForecaster model only.
Like Mdl, holdoutMdl contains three regression models. The crossval function trains holdoutMdl.Learners{1}.Learners{1}, holdoutMdl.Learners{1}.Learners{2}, and holdoutMdl.Learners{1}.Learners{3} using the same training data. However, the three models use different response variables because each model predicts values for a different horizon step.
holdoutMdl.Learners{1}.Learners{1}.ResponseNameans = 'TemperatureF_Step1'
holdoutMdl.Learners{1}.Learners{2}.ResponseNameans = 'TemperatureF_Step2'
holdoutMdl.Learners{1}.Learners{3}.ResponseNameans = 'TemperatureF_Step3'
Compute the root relative squared error (RRSE) on the test data at each horizon step. Use the helper function computeRRSE (shown at the end of this example). The RRSE indicates how well a model performs relative to the simple model, which always predicts the average of the true values. In particular, when the RRSE is less than 1, the model performs better than the simple model.
holdoutRRSE = cvloss(holdoutMdl,LossFun=@computeRRSE)
holdoutRRSE = 1×3
0.4797 0.5889 0.6103
At each horizon, the direct forecasting model seems to perform better than the simple model.
For each test set observation, predict the temperature value using the corresponding model in holdoutMdl.Learners.
predictedY = cvpredict(holdoutMdl); predictedY(450:end,:)
ans=116×3 table
TemperatureF_Step1 TemperatureF_Step2 TemperatureF_Step3
__________________ __________________ __________________
NaN NaN NaN
NaN NaN NaN
NaN NaN NaN
41.063 39.758 41.234
33.721 36.507 37.719
36.987 35.133 37.719
38.644 34.598 36.444
38.917 34.576 36.275
45.888 37.005 38.34
48.516 42.762 41.05
44.882 46.816 43.881
35.057 45.301 47.048
31.1 41.473 42.948
31.817 37.314 42.946
33.166 38.419 41.3
40.279 38.432 40.533
⋮
Recall that only the latest 113 observations appear in the test set. For observations that do not appear in the test set, the predicted response value is NaN.
For each test set, plot the true response values and the predicted response values.
tiledlayout(3,1) idx = test(holdoutPartition); nexttile plot(t(idx),Tbl.TemperatureF(idx)) hold on plot(t(idx),predictedY.TemperatureF_Step1(idx)) legend("True Response","Predicted Response", ... Location="eastoutside") xlabel("Date") ylabel("Temperature") title("Horizon 1") hold off nexttile plot(t(idx),Tbl.TemperatureF(idx)) hold on plot(t(idx),predictedY.TemperatureF_Step2(idx)) legend("True Response","Predicted Response", ... Location="eastoutside") xlabel("Date") ylabel("Temperature") title("Horizon 2") hold off nexttile plot(t(idx),Tbl.TemperatureF(idx)) hold on plot(t(idx),predictedY.TemperatureF_Step3(idx)) legend("True Response","Predicted Response", ... Location="eastoutside") xlabel("Date") ylabel("Temperature") title("Horizon 3") hold off
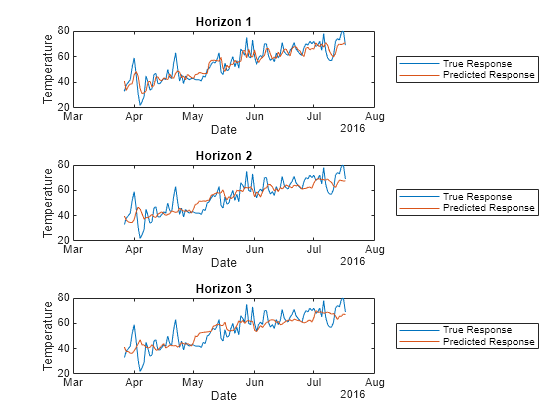
Overall, holdoutMdl is able to predict the trend in temperatures, although it seems to perform best when forecasting one step ahead. If you are satisfied with the performance of the partitioned model, you can use the full DirectForecaster model Mdl for forecasting at time steps beyond the available data.
Helper Function
The helper function computeRRSE computes the RRSE given the true response variable trueY and the predicted values predY. This code creates the computeRRSE helper function.
function rrse = computeRRSE(trueY,predY) error = trueY(:) - predY(:); meanY = mean(trueY(:),"omitnan"); rrse = sqrt(sum(error.^2,"omitnan")/sum((trueY(:) - meanY).^2,"omitnan")); end
More About
Direct forecasting is a forecasting technique that uses separate models to predict the response values at different future time steps (horizon steps). This technique differs from recursive forecasting, where one model is used to predict values at multiple horizon steps.
The software prepares the predictor data for each model and then uses the model to forecast at a particular horizon step.

For more information, see PreparedPredictorsPerHorizon and Horizon.
The directforecaster function accepts data sets with regularly sampled values
that include a response variable and exogenous predictors (optional). That is, the time
steps between consecutive observations are the same. In this context, exogenous predictors
are predictors that are not derived from the response variable.
Consider the following data set.

In this example, the row times in MeasurementTime show that the time difference between consecutive observations is one hour. The times 18-Dec-2015 14:00:00 and 18-Dec-2015 15:00:00 are future time steps that exist beyond the available data. They represent the first and second horizon steps. (See Horizon.)
Suppose the Temp variable is the response variable. The
Pressure, WindSpeed, and
WorkHours variables are exogenous predictors. The
WorkHours variable is a leading exogenous predictor because its
future values are known. (See LeadingPredictors.)
Before fitting a forecasting model, the software creates time-shifted features from the response and exogenous predictors based on user-specified lag values. In this example, the red rectangles indicate a ResponseLags value of 1, PredictorLags value of [1 2 3], and LeadingPredictorLags value of [0 1] at horizon step 1 (18-Dec-2015 14:00:00).
Version History
Introduced in R2023b
See Also
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)