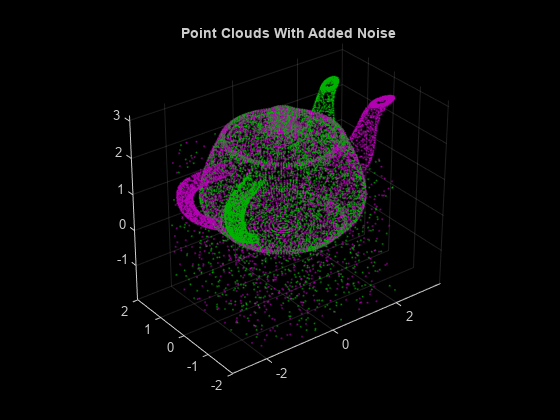
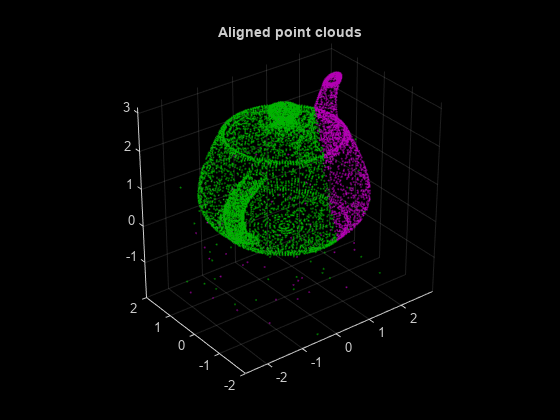
estimateGeometricTransform3D
(Not recommended) Estimate 3-D geometric transformation from matching point pairs
estimateGeometricTransform3D is not recommended. Use the
estgeotform3d function instead. For more information, see Version History.
Syntax
Description
tform = estimateGeometricTransform3D(matchedPoints1,matchedPoints2,transformType)matchedPoints1 to the inliers in the matched points
from the other set of 3-D points matchedPoints2.
[
additionally returns a vector specifying each matched point pair as either an
inlier or an outlier using the input arguments from the previous syntax.tform,inlierIndex]
= estimateGeometricTransform3D(___)
[
additionally returns a status code indicating whether or not the function could
estimate a transformation and, if not, why it failed. If you do not specify the
tform,inlierIndex,status] = estimateGeometricTransform3D(___)status output, the function instead returns an error
for conditions that cannot produce results.
[___] = estimateGeometricTransform3D(___,
specifies additional options using one or more name-value arguments in addition
to any combination of arguments from previous syntaxes. For example,
Name,Value)"Confidence",99 sets the confidence value for finding the
maximum number of inliers to 99.
Examples
Input Arguments
Name-Value Arguments
Output Arguments
Algorithms
The function excludes outliers using the M-estimator sample consensus (MSAC) algorithm. The MSAC algorithm is a variant of the random sample consensus (RANSAC) algorithm. Results may not be identical between runs due to the randomized nature of the MSAC algorithm.
References
[1]
[2]