idwt3
Single-level 3-D inverse discrete wavelet transform
Description
Examples
Create a 3-D array.
X = reshape(1:64,4,4,4); tiledlayout(2,2) for k=1:4 nexttile imagesc(X(:,:,k)) title("k = "+num2str(k)) colorbar end
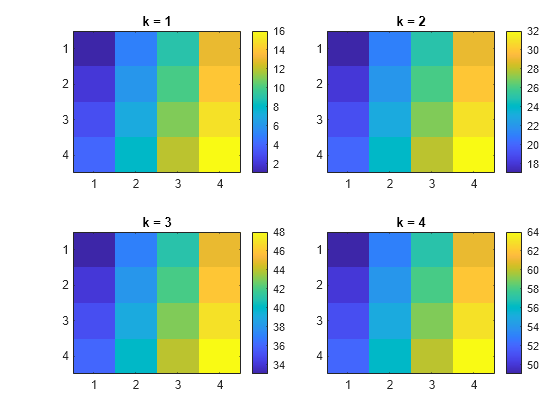
Decompose X using the Haar wavelet.
wt = dwt3(X,"haar");Reconstruct X from the coefficients. Verify that the reconstructed data agrees with the original data to machine precision.
XR = idwt3(wt); dff = max(abs(X(:)-XR(:)))
dff = 3.5527e-14
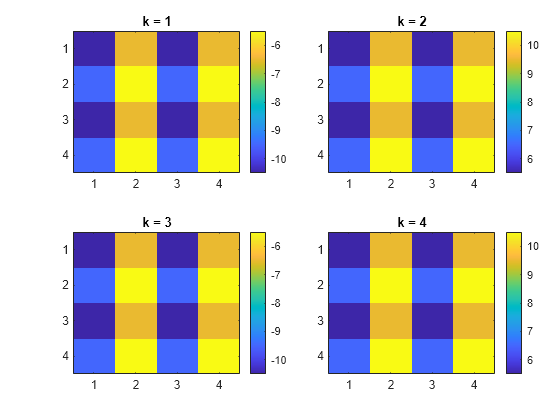
Compute the reconstructed approximation, which consists of the lowpass component.
A = idwt3(wt,"aaa");Compute the sum of all the components different from the lowpass component. Visualize the reconstruction.
D = idwt3(wt,"d"); tiledlayout(2,2) for k=1:4 nexttile imagesc(D(:,:,k)) title("k = "+num2str(k)) colorbar end
Reconstruct the component associated with lowpass in the x and z directions and highpass in the y direction.
ADA = idwt3(wt,"ada");Input Arguments
Single-level 3-D wavelet decomposition, specified as a structure with these fields:
sizeINI | Size of the three-dimensional array
|
mode | Name of the wavelet transform extension mode. |
filters | Structure with four fields:
|
dec | 2-by-2-by-2 cell array containing the coefficients of the decomposition.
The
|
Type of reconstruction, specified as a character vector or string scalar.
Valid values of type are these:
A group of three characters
'xyz', one per direction, with each character selected in the set {'a','d','l','h'} or in the corresponding uppercase set {'A','D','L','H'}, where'A'(or'L') is a lowpass filter and'D'(or'H') is a highpass filter.The char
'd'(or'h'or'D'or'H') gives the sum of all the components different from the lowpass component.
Data Types: char | string
Output Arguments
Reconstruction, returned as a 3-D array.
Reconstructed component of specified type, returned
as a 3-D array.
Version History
Introduced in R2010a
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)