Automatic Tuning of a Helicopter Flight Control System
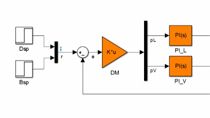
In this video, you will learn how to tune a multivariable flight control system using the Control System Tuner in Simulink. We will use an example of a helicopter flight control system that includes 21 gains to tune, a challenging task made manageable with the Control System Tuner. The system aims to satisfy four key requirements, which range from tracking setpoint changes, to ensuring strong multivariable gain and phase margins, and limiting the speed of closed-loop system dynamics. The Control System Tuner allows the user to specify tuning goals that reflect these requirements, converting them into an optimization problem to automatically tune the controller parameters.
Published: 15 Jun 2023