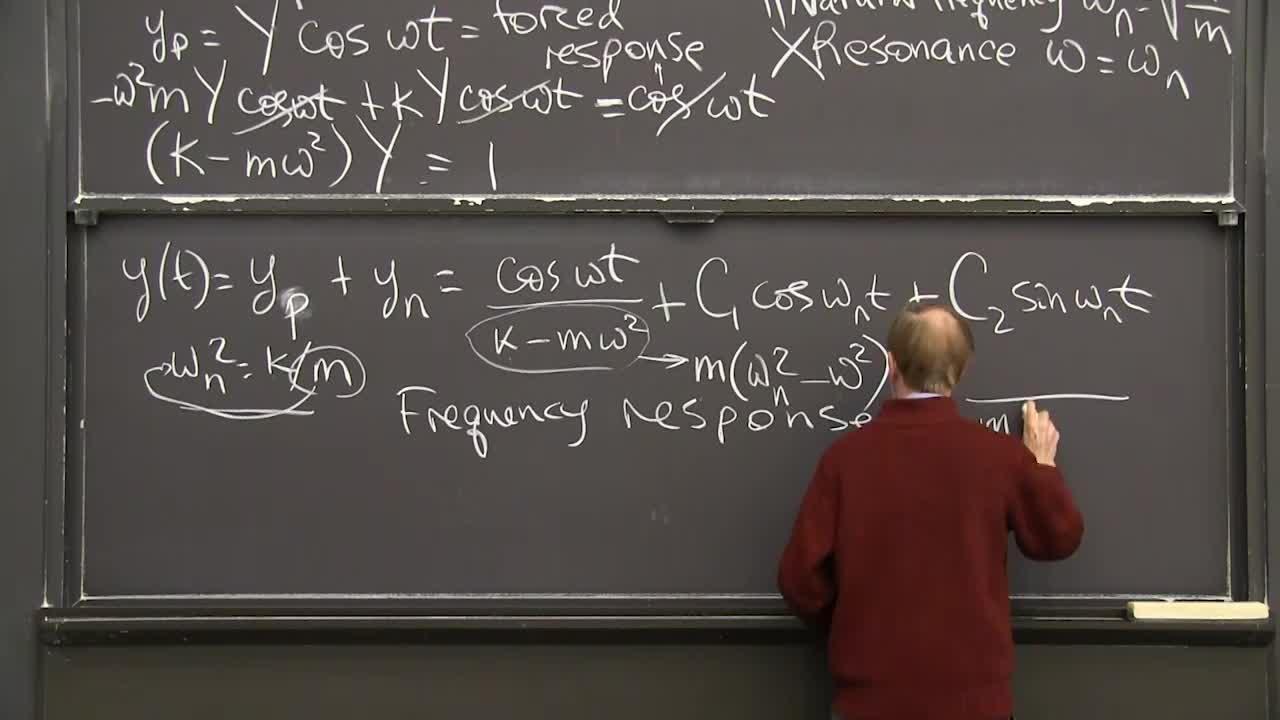Differential Equations and Linear Algebra, 2.1b: Forced Harmonic Motion
From the series: Differential Equations and Linear Algebra
Gilbert Strang, Massachusetts Institute of Technology (MIT)
With forcing f = cos(ωt), the particular solution is Y*cos(ωt). But if the forcing frequency equals the natural frequency there is resonance.
Published: 27 Jan 2016
This is the second video on second order differential equations, constant coefficients, but now we have a right hand side. And the first one was free harmonic motion with a zero, but now I'm making this motion, I'm pushing this motion, but at a frequency omega. This is my forcing term.
So I think I'm having a forcing frequency, omega, and remember that for this one, for the no solution, there was a natural frequency omega n. It's very important are those close, are those well separated? That governs whether the bridge that you're walking over oscillates too much and eventually falls.
Or in the extreme case, are they equal? If omega n is equal to omega that's called resonance. Let me put that word in. Resonance. When omega equals omega n. And we're not going to deal with today, but you should know that always the formula has an omega minus omega n dividing by that. So if that is 0, if omega equals omega n our formula has to change.
Today, this won't happen. No. So what's the formula? What is yp? I'm looking for a particular solution. That's a nice function and also important in practice. So I would like to hope that the particular solution could be some multiple of that cosine omega t.
And in this problem that's possible. Because if I have a cosine, I've got a cosine on the right hand side, and if that cosine comes here, it's on the left side, and the second derivative of the cosine is, again, a cosine, I'm going to have a match of cosine omega t terms. And then I'll just choose the right number capital Y.
I won't be able to do that when there's a first derivative in there, because the first derivative of cosine will bring in signs. I'll have a mixture of cosines and sines and then I better allow for that mixture. But here I don't have to.
There's the forcing function. Response, this is the forced response. I'd like to get used to that word, response, for the solution. Here's the input, the response is the output. So let me just plug that into the equation and find capital Y.
So here I have m, second derivative is going to be a Y, and second derivative will bring out a minus omega squared times the cosine. And here I have kY is Y times the cosine equal the cosine. I could have a constant there, but the whole thing would be no more interesting, no more difficult than with a 1.
So what do I do? The nice thing is here I have all cosines, so I'm just going to have minus omega squared m and a k. So it's k minus m omega squared. Can I write it that way? Times Y. I'm going to cancel the cosines. That's just a 1. On the side is a 1.
I've canceled the cosine, so I've kept kY. I've kept the 1, and I've kept a minus omega squared mY. So that tells me Y right away. It's just like plugging in an exponential and canceling exponentials all the way along. Here, I'm canceling cosines all the way because every term was a cosine.
So I know Y. So I know the answer. So the final answer is Y(t) is Yn. Well, let me put Y particular first plus Yn. So I've just found Y particular. Y particular is this capital Y cosine omega t. So it's cosine omega t times Y and Y is 1 over this.
Here's goes Y. Down below I have k minus m omega squared. Right? That's what we just found, that particular solution. The capital Y, the multiplying constant, was 1 over that constant. And now comes the C1 cosine of omega nt and the C2 sine of omega nt.
Remember, omega n is different from omega. Actually, this is pretty nice here. I could write that another way so you would see the important here. So remember, what is omega n squared? Can I just remember that omega n squared is k over m. Right? Yup.
k is the same as-- I'm going to put that m up here-- k is the same as m omega n squared. k is the same as m omega n squared and here I'm subtracting m omega squared. You'll see the whole point of resonance or near resonance when the bridge is getting forced buy a frequency close to its resonant frequency.
This difference, omega squared, the difference between the two frequencies squared is in the denominator and will be small and then the effect is large. And if we get those too close, the effect is too large. So we'll see this cosine omega t over this is, I would call, the frequency response is this factor. 1 over m omega n squared minus omega squared.
That's the key multiplier for when the forcing term is a pure frequency, that frequency gets exploded. And now, of course, what are capital C1 and capital C2? We find those from the initial condition. At t equals 0, we put in t equals 0, and that tells us what C1 has to be. And we put in t equals 0 again to match the velocity Y prime at 0, and that tells us C2. Are you OK with that?
Just look at the beauty of that solution. This is null part. This is the forced part, the particular part, the cosine divided by that constant. There's one more equation, one more forcing term I'd like often and always and now to discuss. And that is a delta function, an impulse.
So I'm going to add one more example. my double prime plus ky equal the delta function. Delta function. It's called an impulse. So I'd like to solve that equation also. When the forcing term just happens at one second, at the initial second. At t equals 0, the delta function, I'm hitting the spring.
So the spring is sitting or the pendulum is sitting there. Actually, let's set it at rest. Here's my pendulum. I'll try to draw a pendulum. I don't know. That's not much of a pendulum. But it's good enough.
This equation says what happens if I hit it with a point source? At t equals 0, I hit it but I give it a finite velocity. It doesn't move in that instant second. This is where delta functions come in so let me give you the result of what happens and then we'll see them again.
So what am I doing? I want to solve this equation when the forcing function is a delta function. So I'm going to call y the impulse response. It's the solution that comes when the forcing function is an impulse. So y is the impulse response. In fact, it's so important, I'm going to give it its own letter. g. Now, can I turn that y into a g?
So that g is g of t is the impulse response. If I can solve that equation. You might say, not so easy. With a delta function, it's not even a genuine function. It's a little bit crazy. It all happens in one second. I'm sorry, in one instant. Not over one second, but one moment.
But I can solve it. I can solve it for this reason. I can think of it as an impulse here or I have an option, another way which clearly I can think of it as solving it with no force mg double prime. Same problem, same solution is 0.
But I start from rest. Nothing's happening. y of 0 is 0. And it starts from an initial velocity, y prime of 0. The impulse starts it out like a golf ball. Just go. And there's a 1 over m there. I'll discuss that another time.
What I want to see now is that I have either this somewhat mysterious equation or this totally normal equation, even a no equation starting from y of 0 equals 0. But with an initial velocity that the impulse gave to the system. And I should be calling this g. This is the g. We'll see impulse responses again, but let's see it this time by solving this equation.
So I plan to solve that equation and actually we solved it last time. You remember the solution to this one? When it starts from 0, there's no cosine. But when the initial velocity is 1 over m, there is a sign. So I'm going to just write down the g of t, which is just sine of omega nt.
And why is it the natural frequency? Because I'm solving the no. I'm looking for a no solution. But the previous video on no solutions gets me this. Only I have to divide by, get 1 over m as the initial velocity. You'll see that that will solve the no equation.
This is what happens to the pendulum or the golf ball. Well, pendulum much better. Actually, golf ball is poor example. Sorry about that. Golf balls don't swing back and forth. They tend to go.
I'm looking at pendulums, springs going up and down. So the spring starts out, has an initial velocity of 1 over m and then after that nothing happens. So that is the impulse response. The response to an impulse. And why do I like that? First of all, its beautiful. Simple answer.
Secondly, every forcing function, and the output comes from this one. We'll see that point. So we've introduced forcing functions, cos omega t, where the particular solution was a multiple of cos omega t. And now, we've introduced a forcing function delta, the delta function where the response is a sine function. Thank you.