Accelerating Finite Element Analysis in MATLAB with Parallel Computing
By Vaishali Hosagrahara, MathWorks, Krishna Tamminana, MathWorks, and Gaurav Sharma, MathWorks
The Finite Element Method is a powerful numerical technique for solving ordinary and partial differential equations in a range of complex science and engineering applications, such as multi-domain analysis and structural engineering. It involves decomposing the analysis domain into a discrete mesh before constructing and then solving a system of equations built over mesh elements. The number of equations involved grows as the mesh is refined, making the Finite Element Method computationally very intensive. However, various stages of the process can be easily parallelized.
In this article we perform coupled electro-mechanical finite element analysis of an electrostatically actuated micro-electro-mechanical (MEMS) device. We apply parallel computing techniques to the most computationally intensive part of the mechanical analysis stage. Using a 40-worker1 setup, we will reduce the time taken for the mechanical analysis with an approximately one-million DOF mesh from nearly 60 hours to less than 2 hours.
MEMS Devices
MEMS devices typically consist of thin, high-aspect ratio, movable beams or electrodes suspended over a fixed electrode (Figures 1 and 2). They integrate mechanical elements on silicon substrates using microfabrication.

Figure 1. MEMS-based accelerometer. Image courtesy MEMSIC Inc.

Figure 2. Electrostatic comb drive. Image courtesy Compliant Mechanisms Research Group, Brigham Young University.
The electrode deformation caused by the application of voltage between the movable and fixed electrodes can be used for actuation, switching, and other signal and information processing functions.
FEM provides a convenient tool for characterizing the inner workings of MEMS devices so as to predict temperatures, stresses, dynamic response characteristics, and possible failure mechanisms.
One of the most common MEMS switches is the cantilever series (Figure 3). This consists of beams suspended over a ground electrode.

Figure 4 shows the modeled geometry. The top electrode is 150μm in length, and 2μm in thickness. Young’s modulus E is 170 GPa, and the Poisson ratio υ is 0.34. The bottom electrode is 50μm in length, 2μm in thickness, and located 100μm from the leftmost end of the top electrode. The gap between the top and bottom electrodes is 2μm.

When a voltage is applied between the top electrode and the ground plane, electrostatic charges are induced on the surface of the conductors, which give rise to electrostatic forces acting normal to the surface of the conductors. Since the ground plane is fixed, the electrostatic forces deform only the top electrode. When the beam deforms, the charge redistributes on the surface of the conductors. The resultant electrostatic forces and the deformation of the beam also change. This process continues until a state of equilibrium is reached.
Applying FEM to Coupled Electro-Mechanical Analysis
For simplicity, we will use the relaxation-based algorithm rather than the Newton method to couple the electrostatic and the mechanical domains2. The steps are as follows:
1. Solve the electrostatic FEA problem in the nondeformed geometry with constant potential V0 on the movable electrode.
2. Compute load and boundary conditions for the mechanical solution using the calculated values of the charge density along the movable electrode.
The electrostatic pressure on the movable electrode is given by \[P=\frac{1}{2\epsilon}|D|^2\]
Where,
\(|D|\) = Magnitude of the electric flux density
\(\epsilon\) = Electric permittivity next to the movable electrode
3. Solve the mechanical FEA to compute the deformation of the movable electrode.
4. Using the calculated displacement of the movable electrode, update the charge density along the movable electrode.
\[\left|D_{\mathrm{def}}(x)\right| \approx \left|D_0(x)\right|\frac{G}{G - v(x)}\]
Where,
\(|D_{\mathrm{def}}(x)|\) = Magnitude of the electric flux density in the deformed electrode
\(|D_0(x)|\) = Magnitude of the electric flux density in the undeformed electrode
\(G\) = Distance between the movable and fixed electrodes in the absence of actuation
\(v(x)\) = Displacement of the movable electrode at position x along its axis
5. Repeat steps 2 – 4 until the electrode deformation values in the last two iterations converge.
The electrostatic analysis (step 1) involves five steps:
- Draw the cantilever switch geometry.
- Specify the Dirichlet boundary conditions as a constant potential of 20 V to the movable electrode.
- Mesh the exterior domain.
- Solve for the unknown electric potential in the exterior domain.
- Plot the solution (Figure 5).

We can quickly perform each of these tasks via the Partial Differential Equation Toolbox™ interface.
Mechanical Analysis
The mechanical analysis involves five steps:
- Meshing the domain
- Deriving element-level equations
- Assembly
- Imposing boundary conditions
- Solving the equations
Meshing the Domain
In this step we discretize the system domain into smaller domains, or elements. Discretization lets us represent the geometry of the domain and approximate the solution over each element to better represent the solution over the entire domain. The number of elements determines the size of the problem.
Deriving Element-Level Equations
In this step, we assume an approximate solution for the differential equations over an element at selected points, or nodes. In our example, the solution is determined in terms of discrete values of \(\phi\) displacements in the \(x\) and \(y\) directions (2D analysis). The number of unknown primary fields at a node is called the degrees of freedom (DOF) at that node.
The governing differential equation is now applied to the domain of a single element (Figure 6). At the element level, the solution to the governing equation is replaced by a continuous function approximating the distribution of \(\phi\) over the element domain \(D^e\), expressed in terms of the unknown nodal values \(\phi_1\), \(\phi_2\), and \(\phi_3\) of the solution \(\phi\). A system of equations in terms of \(\phi_1\), \(\phi_2\), and \(\phi_3\) can then be formulated for the element.
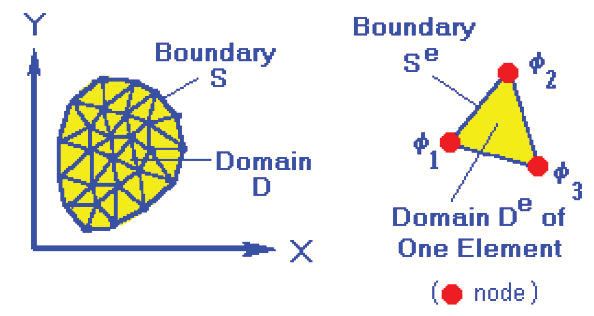
Assembly
We obtain the solution equations for the system by combining the solution equations of each element to ensure continuity at each node. In our example, the element-level stiffness and force matrices (\(K_e\) and \(F_e\)) are assembled to create a global stiffness matrix (\(K\)) and a force matrix (\(F\)) over the entire domain
Imposing Boundary Conditions
We impose the necessary boundary conditions at the boundary nodes and solve the global system of equations. The solution \(\phi(x,y)\) to the problem becomes a piecewise approximation, expressed in terms of the nodal values of \(\phi\). A system of linear algebraic equations results from the assembly procedure: \(K \phi = F\).
It is not uncommon for practical engineering problems to have a system containing thousands of equations. Parallel computing techniques can greatly reduce the time required to assemble the matrices and compute the solution for problems of such massive size.
Solving the Equations
We solve the global system of equations \(K \phi = F\) for the displacements in the \(x\) and \(y\) directions.
Parallelizing the Problem
We implement each step defined in the Finite Element Method in a MATLAB® function. Meshing is done using mesh2d, a MATLAB based mesh generation application for 2D geometries. The Profiling tool in MATLAB shows that the most time-consuming operations belong to the stiffness matrix assembly step.
This step involves three main operations for each element:
1. Compute the element stiffness matrix (\(K_e\)) from the element-level solution equations. \(K_e\) is of size \(N_e \times N_e\)
Where,
\(N_e\) is the number of DOF per element
\(n\) is the number of nodes per element
\(D\) is the number of DOF per node
2. Map the local positions of the \(K_e\) matrix values to their position in the global stiffness matrix.
3. Populate the global stiffness matrix (\(K\)) using the map with the element stiffness matrix values.
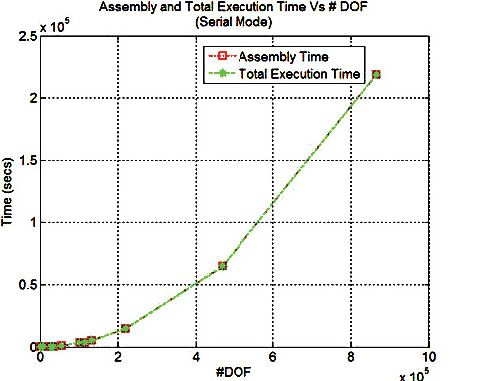
| Number of Elements | Degrees of Freedom (DOF) | Assembly Time (seconds) | Total Execution Time (seconds) | Assembly Time/ Total Execution Time (%) |
|---|---|---|---|---|
| 528 | 806 | 4.09 | 4.82 | 84.5 |
| 6584 | 7690 | 45.073 | 46.371 | 97.2 |
| 53550 | 55882 | 960.069 | 1005.448 | 95.5 |
| 460752 | 469566 | 64573.472 | 64616.662 | 99.9 |
Table 1. Comparison of assembly time and total execution time for different DOF.
As the number of elements increases, so do the number of iterations and the size of \(K\). Figure 7 and Table 1 compare the time taken for assembly to the total execution time in serial mode for the system with different DOF. Clearly, assembly is the most time-consuming portion, taking up more than 99% of the total execution time when the system has high DOF.
Stiffness Matrix Assembly
Fortunately, the final assembled \(K\) matrix is independent of the order in which the elements are chosen within the loop. We can evaluate the contributions of several elements to global stiffness matrix (\(K\)) simultaneously by distributing the computations across multiple MATLAB workers. The assembly operations are normally executed in a serial for-loop, which steps through each element and determines its contribution to the global stiffness matrix. We simply convert the serial for-loop to a parallel for-loop using the parfor construct in Parallel Computing Toolbox™ (Figure 8).
In our example, the global stiffness matrix is the sum of the contributions of the element stiffness matrices across all the iterations of the loop. The parfor construct enables us to handle such reduction assignments (usually of the form \(r = f(\text{expr}, r)\)) automatically.
To demonstrate the performance gains achieved by using a parallel approach, the problem was scaled up from coarse mesh to a super-refined mesh. The coarse mesh contained about 128 elements with a total of 150 DOF. We refined the mesh until it contained 856,800 elements with 861,122 DOF. As we refined the mesh, the displacement of the free end of the cantilever beam converged
For the parallel approach, we used a computer cluster with one head-node and 5 machines, each with the following configuration: Dual Intel® Xeon® 1.6 GHz quad-core processor (8-cores per machine for a total of 40 cores), 13 GB RAM with Windows® 64-bit operating system. Each machine ran 8 MATLAB workers for a total of 40 workers. To measure the serial execution time, we used a single MATLAB worker running on the head node. Using a 64-bit OS enabled us to create large sparse matrices (up to 861,122 x 861,122) without running into memory limitations. In most finite element applications, the resultant K is sparse in nature.
Figures 9a and 9b compare the total execution time in seconds with increasing DOF between the serial (red) and parallel (green) modes of execution. Table 2 summarizes the results.


| Degrees of Freedom (DOF) | Total Execution Time (seconds) | |
|---|---|---|
| Serial Mode | Parallel Mode | |
| 150 | 0.53 | 1.15 |
| 250 | 0.77 | 1.18 |
| 806 | 4.82 | 1.37 |
| 2200 | 12.93 | 2.8 |
| 7690 | 46.37 | 6.1 |
| 28546 | 355.04 | 20.92 |
| 103822 | 3406.61 | 129.23 |
| 218862 | 14871.7 | 496.47 |
| 469566 | 64616.66 | 1911.71 |
| 866122 | 218674.88 | 6237.91 |
Table 2. Representative data used in Figures 9a and 9b.
Notice that for a system with few DOF, the cost of distributing the operations is much higher compared to the execution times of these operations. As a result, when the system had only 250 DOF, serial execution was actually faster than the parallel execution.
Figure 9b shows that up to about 400 DOF, the point where the two curves intersect, the serial mode execution is faster than the parallel mode. We see a performance improvement by switching to parallel mode only after this point. The actual execution time and cross-over point depend on several factors, including the execution speed of the MATLAB functions involved, the processing speed of the worker machines, network speed, and number of workers, available memory, and system load.
Summary
In this article we demonstrated a simple approach to parallelizing an FEA application. We began by analyzing serial code performance, focusing on the most computationally intensive part of our setup. With simple code changes we were able to significantly boost our application performance, cutting down time for analyzing an 800,000DOF system from 60 hours to less than 2 hours on a 40-worker setup.
1 Workers are MATLAB computational engines that run separately from your MATLAB session.
2 P.S. Sumant, N.R. Aluru and A.C. Cangellaris, “A methodology for fast finite element modeling of electrostatically actuated MEMS.” International Journal for Numerical Methods in Engineering 2009; 77:1789-1808.
Published 2010 - 91826v00
