Battery Fast Charge with Simscape Battery and About:Energy
By Darryl Doyle and Yashraj Tripathy, About:Energy; Steve Miller and Sebastián Arias, MathWorks
Integrating About:Energy TSPMe and electrical models with detailed pack models enabled by Simscape Battery ensures accuracy and safety in battery management systems, augmenting ongoing advancements in the field of battery charging.
Battery fast-charge time is a key performance indicator in the design of electric vehicles (EVs) and a key concern of EV customers. This article demonstrates how to generate safe and robust fast-charge profiles for different battery system sizes using Simscape Battery™, along with custom cell model blocks and parameters developed by About:Energy. This includes DC Level-1 (up to 80 kW) and Level-2 (up to 400 kW, also referred to as Level-3) battery fast-charge profiles according to SAE J1772. This article also shows how to scale up custom battery cell models using Simscape™ and the Battery Pack Builder workflow from Simscape Battery (Figure 1).
Several processes inside an EV lithium-ion battery cell affect the maximum rate at which the cell can charge such as lithium diffusion in the negative electrode and lithium-ion transport in the electrolyte. These processes take place at a microscopic scale and are governed by local temperature, state of charge (SOC), and state of health (SOH) of individual battery cells, as well as cell chemistry. Other factors also come into play at the battery module and pack levels, such as system and DC charger current limits, intercell temperature spreads due to thermal management strategy, SOC spreads due to electrical design, control strategy, sensor placement, non-cell electrical resistance, and manufacturing variability. These additional factors can limit fast-charge rates even further. Therefore, it is crucial to consider all these variables in any battery design and validation workflows.
Battery Cell Models
The Battery Builder functionality in Simscape Battery enables automated creation of battery module and pack models from user-defined Simscape blocks of a single battery cell, including battery cell blocks provided by About:Energy. In this article, we show two types of previously validated battery models of a nickel-rich, high-energy 2170 cell provided by About:Energy:
- A thermal single-particle model with electrolyte (TSPMe), which provides access to internal electrochemical states or variables required for performing tasks such as fast charge control.
- An equivalent circuit model (ECM) parameterized specifically for fast charge, which provides relatively faster computation times once it has been scaled up to the module or pack level.
The Simscape Battery library also contains battery cell model blocks that use the equivalent circuit approach and an electrochemical single-particle model (Figure 2). These have been available in Simscape Battery since R2023b and R2024a.
Cell-to-Module Worked Example
We can use the battery builder functionality in Simscape Battery to rapidly prototype battery system models and evaluate battery fast-charge times for different subcomponent levels under a wide range of thermal and electrical boundary conditions and initial operating states (SOC and temperature).
First, we must define a battery cell object and link this cell object to the corresponding cell model block provided by About:Energy. We first scale up the ECM. To use the ECM block, we first load electrothermal parameters provided by About:Energy, which are contained in a structure named cellData.
run("CellModelParameters.mlx") % Load cell ECM parameters (e.g., capacity, energy)
To define the battery cell object, we must instantiate the Cell class from the Battery Builder package in Simscape Battery as follows:
import simscape.battery.builder.* % Import battery builder package battCell = Cell(Geometry = CylindricalGeometry(... 'Height',simscape.Value(cellData.cellHeight,'m'),... 'Radius',simscape.Value(cellData.cellRadius,'m')), ... Capacity = simscape.Value(cellData.cellCapacity,"A*hr"), ... Energy = simscape.Value(cellData.cellNominalEnergy,"W*hr")); % Cell object
We can link our battery cell object to About:Energy custom blocks by modifying the CellModelOptions property as follows:
battCell.CellModelOptions.CellModelBlockPath = "AE_Mathworks_lib/AE_mathworks_ECM"; disp(battCell.CellModelOptions) CellModelBlock with properties: CellModelBlockPath: "AE_Mathworks_lib/AE)_mathworks_ECM" BlockParameters: [1x1 struct]
For this example, we create a 400-volt automotive-style traction battery made up of 16 battery modules. Each battery module consists of 36 cylindrical cells connected electrically in parallel and then six of these parallel assemblies connected electrically in series (36p6s). The code to scale up the cell component into a parallel assembly and then into a module is shown below:
battPSet = ParallelAssembly(Cell = battCell, NumParallelCells = 36,... Rows = 9, ModelResolution="Detailed",... NonCellResistance = "on",... AmbientThermalPath="CellBasedThermalResistance", ... CoolantThermalPath="CellBasedThermalResistance",... CoolingPlate="Bottom"); % Parallel assembly object battModule = Module(ParallelAssembly = battPSet, NumSeriesAssemblies = 6,... NonCellResistance = "on",... ModelResolution="Grouped",... SeriesGrouping = [1,4,1],... ParallelGrouping = [36,1,36],... AmbientThermalPath="CellBasedThermalResistance", ... CoolantThermalPath="CellBasedThermalResistance",... CoolingPlate="Bottom"); % Module object
Alternatively, we can also define this same battery design and objects using the Battery Builder app (Figure 3).
We can automatically generate Simscape models from the battery objects defined above by calling the buildBattery function. When calling this function, we can also define the MaskParameters name-value pair to “VariableNamesByType” to generate a script with all the parameters required to run the model. Prior to model creation, we can verify our battery definition and design by using the BatteryChart object, which helps visualize the geometry and positioning of the battery cells in a 3D space. Table 1 showcases the typical outputs from the usage of these functions for our module and parallel assembly objects.
| Battery Visualization Code | Battery Model Creation Code |
f = uifigure(Color="w");
BatteryChart(Battery=battPSet);
|
buildBattery(battPSet, Library= "detailedPSet",... MaskParameters = "VariableNamesByType"); |
f = uifigure(Color="w");
BatteryChart(Battery=battModule);
|
buildBattery(battModule, Library= "groupedModule",... MaskParameters = "VariableNamesByType"); |
Next, we define the fast-charge electrical load, which is used to test the generated battery models. To accomplish this, we must first estimate the battery cell fast-charging capability.
Cell-Level Fast Charge
During a fast-charging event, there is a higher risk of lithium plating depending on the operating conditions of the battery and its electrochemistry. Ultimately, the key driving force behind lithium plating is the local potential difference between the solid and liquid phases at the anode electrolyte interface, which is affected by many factors, such as temperature, diffusion limitations, SOC, and charging rate. Cold temperatures generally lead to sluggish transport phenomena and bigger potential differences during charging. Therefore, intracell temperature and SOC differences will naturally cause different regions of the cell to be more at risk of lithium plating. These differences will always be present given a specific cell design and the thermal boundary conditions surrounding the cell. Table 2 presents the key internal variables and boundary conditions that must be considered to derive a safe and fast charge profile.
| Variable | Description & Code |
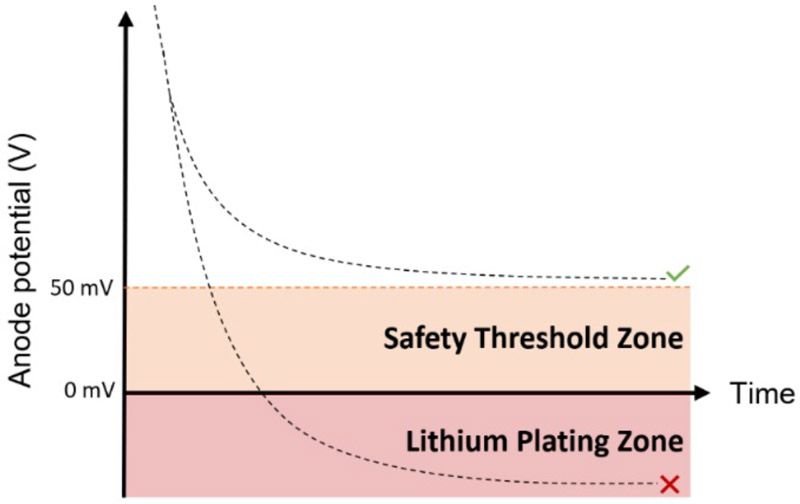
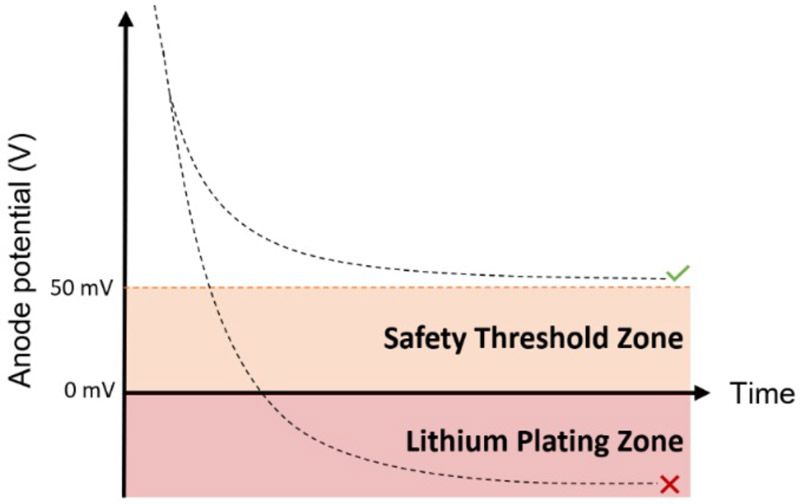
| Anode potential | We will use the electrostatic potential of the negative electrode with respect to a Li/Li+ reference electrode as an indicator for increased risk of lithium plating and accelerated degradation. During charging, this potential falls due to the mass transport and chemical reaction processes happening inside the cell. To reduce the risk of lithium plating, this potential must not fall too far below 0 V. In this example, this potential threshold will be arbitrarily set to 50 mV.
AnodePotentialThreshold = 0.05; % Unit: V
|
| Battery temperature | Cell temperature must remain below its operational limit to limit degradation and reduce risk of thermal runaway. TemperatureThreshold = 55 + 273.15; % Unit: K
|
| Initial battery temperature | Warmer temperatures allow for higher currents. If the maximum operating temperature is reached, this will cause the control system to derate the current and lengthen charge time. Colder initial temperatures provide more temperature delta for dampening the high heat generation, but colder temperatures also limit the maximum current. Therefore, an optimal initial temperature exists, and it can be found using simulation or physical testing. InitialCellTemperature = 35 + 273.15; % Unit: K
|
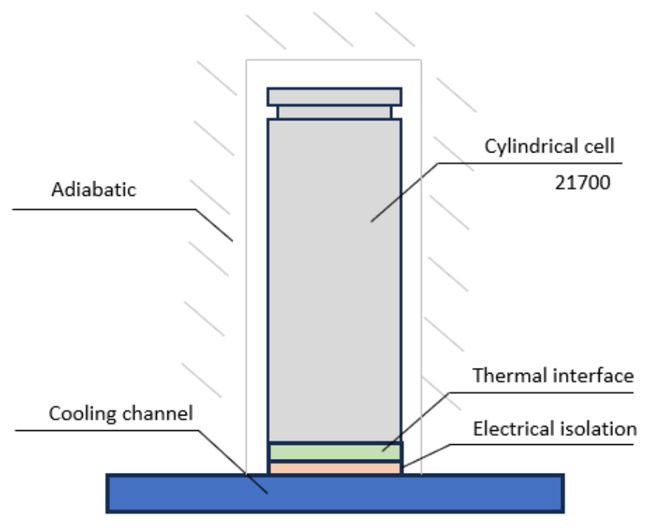
| Thermal management boundary conditions | In this example, we consider a “bottom-cooled” battery cell potted to a cooling plate as shown in the following diagram. We will assume a constant 5 K/W of thermal resistance defined from the cell bottom surface to the bulk coolant in the cooling channel.
CellThermalPathResistance = 5; % Unit: K/W
|
| Battery terminal voltage | During charging, the cell voltage increases. To prevent overvoltage or overcharge conditions, the battery voltage cannot exceed the maximum specified by the cell supplier. MaximumBatteryVoltage = 4.2; % Unit: V
|
| Fully charged battery | At the end of the charging phase, the terminal voltage rises toward its maximum level. To assure an optimal fast charge and avoid overcharge conditions, the current must be reduced in a constant voltage step (CV). In this article, the fully charged (100% SOC) condition is reached once the current value falls below 1/10 the rated cell capacity. FullyChargedCurrentThreshold = cellData.cellCapacity/10; % Unit: A
|
| Maximum charge current | This value should be specified by the battery manufacturer for a specific set of conditions (SOC, SOH, temperature). In general, batteries can accept higher charging currents for short amounts of time and smaller charge current for longer periods of time. MaximumChargeCurrent = 30; % @ 0% SOC, instantaneous limit, Unit: A
|
Fast-Charge Profile Methodology
To monitor the anode potential across the entire jelly roll, a height-discretized electrothermal cell level model was created using Simscape language and the About:Energy TSPMe model as the basis (Figure 4). The thermal model is discretized along the height to capture the thermal gradients that arise from base cooling. The discretized elements are connected electrically in parallel and thermally in series in a way that replicates the cell internals and allows for a higher internal state resolution. Higher and more accurate state resolutions can be achieved by also dividing up the elements radially. About:Energy also provides Simscape 2D thermal model blocks.
Three PI controllers derate the maximum allowable current and maintain safe operational conditions (Figure 5):
The derivation of the optimal charge current uses this strategy (Figure 6):
- Charge the battery at the fastest rate allowable by the supplier at 0% SOC and the selected initial temperature.
- Derate the current if the anode potential reaches its specified threshold value.
- Derate if the hottest spot on the battery cell reaches the maximum operational temperature.
- Derate if the terminal voltage reaches the maximum voltage limit to prevent overcharge.
- If necessary, add other derating conditions based on other states, such as the lithium concentration in the electrolyte.
- Charging stops once the constant voltage step reaches C/10.
- Store the final delivered current signal as your final fast-charge current profile.
cellSimulation = sim("CellLevelFastCharge.slx","StartTime","0","StopTime","3600"); run("PlotCellSimulation.mlx");
Table 3 summarizes the discretized cell-level simulation results given our assumptions.
| SOC Window | Fast-Charge Time (min) | Conditions |
| 0–80 % | 14 | @ 35 °C initial temperature, BoL, and assumed constraints |
| 0–100 % | 30 | @ 35 °C initial temperature, BoL, C/10 CV condition |
Cell Fast-Charge Map
The fast-charge controller established in the previous section will output a current profile that is only valid for the assumed initial temperature and SOC and does not consider nonuniformities in the initial or dynamic values of these states. We can derive a more general two-dimensional map of the maximum charging current as a function of temperature and SOC (at beginning of life) by running multiple simulations at different initial conditions.
Using Stateflow® logic, for every set of initial conditions, we can run a simulation where we quickly ramp up the current from zero amps until we reach the anode potential threshold or the terminal voltage threshold (Figure 7). When one of these thresholds is reached, we derate the current to maintain the limiting variable constant at its threshold for a given duration. In this article, this duration will be arbitrarily defined at 60 seconds (sometimes known as a continuous limit) to mimic an event of long duration such as a charge.
In general, longer durations translate into lower or more restrictive current limits. The simulation stops at the given timeframe and then we save the final current value as the limit (Figure 8). The resulting map can be used as an input to our previously defined system-level simulations, which do not have access to the internal electrochemical states like the anode potential(s).
InitialCellTemperatureVector = [5,15,25,35,45,50] + 273.15; % Unit: K InitialSOCVector = [0,0.05,0.1,0.2,0.5,0.6,0.8,0.95]; % Unit: - for initTempIdx = 1:numel(InitialCellTemperatureVector) for initSOCIdx = 1:numel(InitialSOCVector) InitialCellTemperature = InitialCellTemperatureVector(initTempIdx); InitialSOC = InitialSOCVector(initSOCIdx); cellSimulations(initTempIdx).SOCPoint(initSOCIdx).Data = sim("CellLevelFastChargeLimitsStateFlow.slx","StartTime","0","StopTime","60"); cellCurrentLimit(initTempIdx,initSOCIdx) = cellSimulations(initTempIdx).SOCPoint(initSOCIdx).Data.simout.Data(end); save cellCurrentLimit end end newCellCurrentLimit = [cellCurrentLimit, zeros(1,numel(cellCurrentLimit(:,1)))']; figure("Color","w") [xq,yq]= meshgrid([5:1:50]+273.15, 0:0.05:1); vq = griddata(InitialCellTemperatureVector,[InitialSOCVector,1],newCellCurrentLimit',xq,yq); mesh(xq,yq,vq) xlabel('Temperature (°C)') ylabel('State of Charge (-)') zlabel('Current Limit (A)') view([-5 3.5 5])
Parallel Assembly–Level Fast Charge
When manufacturing EV battery packs, a battery cell is typically first connected electrically in parallel to other cells to form a parallel assembly, thus scaling up battery capacity and energy. To calculate the fast-charge profile for a parallel assembly subsystem, we simply need to multiply the obtained cell fast-charge profile by the number of cells in parallel. Depending on this number P, the resulting fast-charge current might exceed the maximum current limit of common battery DC chargers present at charging stations. This is an important constraint to keep in mind when trying to predict system-level fast-charge times.
Given a specific battery energy with a fixed total number of cells, 400-volt battery packs will typically have a higher number of cells connected in parallel than 800-volt systems. If we want to make use of the optimal cell fast-charge profile derived in the first section, then it follows that the higher number of cells in parallel will translate into higher fast-charge currents. For typical 400-volt systems, higher currents or P numbers mean that they are more likely to be constrained by the charger station (when starting the charge at 0% SOC). This limitation can lead to untapped cell fast-charging capability and slower charging rates. Table 4 shows typical maximum currents for different DC EV chargers.
| Typical Off-Board Charger Power | Typical Maximum Continuous Current |
| 100 kW | 100–250 A |
| 350 kW | 350–500 A |
Figure 9 shows the supercharger current limit of 500-amp versus typical scaled-up, parallel assembly–level fast-charge profiles for typical 400-volt and 800-volt systems. As higher numbers of cells in parallel are related to 400-volt systems (for a given battery energy), we will arbitrarily define a “36 P” parallel assembly as representative of a 400-volt system. Then we will compare this system against an “18 P” parallel assembly, representative of an 800-volt system at 35 °C.
run("parallelAssemblyProfile.m")
As shown in the plot, the 400-volt system will not be able to initially make use of all the charging capability of the cell, which might lead to slower charging times than the predicted 0–80% in 14 minutes.
In general, the rate of charge for an assembly of batteries connected electrically is governed by the coldest spot on the coldest cell and the highest SOC spot inside the cell with the highest SOC. Therefore, the fast-charge control will be based on the minimum cell temperature and the highest SOC signals obtained from the parallel assembly plant model.
Battery cells are typically laid out on top of a thermal interface material that is in contact with the cooling plate (which also contains a layer of electrical isolation). We will define a random variation in this thermal path by assuming some unevenness (e.g., application of thermal interface material between cells and a cooling plate).
ParallelAssembly1.CoolantResistance = 14 + (30-14)*rand(36,1)'; % Cell level coolant thermal path resistance, K/W
Other important aspects to consider that can be modeled with Simscape but are not explicitly covered in this article are:
- Cell-to-cell internal resistance and capacity variabilities from cell manufacturing.
- Collector plate design can cause slight current imbalances if not designed properly.
- Different thermal paths to ambient (these dynamics are usually slower).
- Coolant control: Normally, electric vehicles would have a fixed chiller or cooling capability (e.g., 5 kW) for heat removal from the battery system (and other components). A realistic coolant control will also have an important effect on the battery fast-charge time.
We can integrate our parallel assembly block into Simulink® and add the scaled-up 2D charge map we have just derived with the cell electrochemical capability. We have also added a PI controller to limit the maximum cell temperature in the parallel assembly (Figure 10).
Run the parallel assembly simulation and plot the results (Figure 11).
run("detailedPSet_param.m"); set_param("ParallelAssemblyLevelFastCharge","SimscapeLogType",'all') pSetSimulation = sim("ParallelAssemblyLevelFastCharge.slx","StartTime","0","StopTime","5200"); run("PlotParallelAssemblySimulation.mlx"); % Plot results
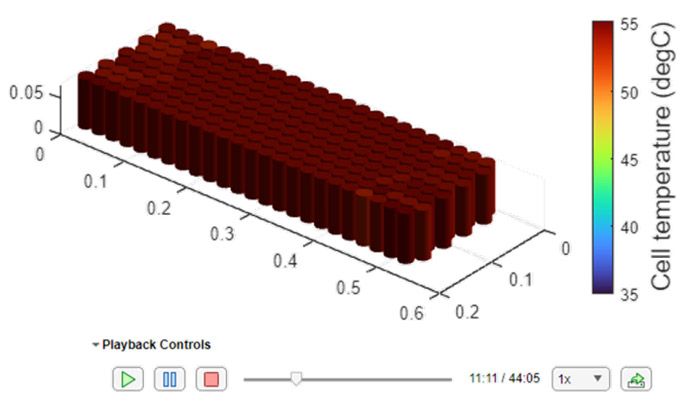
As shown in the summary plot, the parallel assembly is constrained by the charger 500-amp maximum current at the beginning of the simulation. In addition, the hottest cell temperature reaches 55 °C, triggering a thermal derate that slows down the simulation time. To visualize the battery dynamic temperatures, we can create battery simulation log object as shown in the following code (Figure 12).
pSetSimLog = BatterySimulationLog( battPSet, pSetSimulation.simlog.ParallelAssembly1); pSetSimLog.SelectedVariableUnit = "degC"; f = uifigure("Color","w"); g = uigridlayout(f, [1,1]); parallelAssemblyChart = BatterySimulationChart(Parent = g, ... BatterySimulationLog = pSetSimLog); parallelAssemblyChartColorBar = colorbar(parallelAssemblyChart); ylabel( parallelAssemblyChartColorBar, strcat("Cell temperature", " (", pSetSimLog.SelectedVariableUnit,")") ,'FontSize',14 ); parallelAssemblyChartColorBar = colormap(parallelAssemblyChart);
As shown in the dynamic battery plot, there is an approximate 5 °C temperature difference between the cells. The difference is mainly due to the random variation in thermal path to the coolant assumption. Table 5 shows the parallel assembly simulation results. The 0–80% SOC fast-charge times have increased by 10 minutes mainly due to the system-level limitation and thermal assumptions.
| SOC Window | Fast-Charge Time (min) | Conditions |
| 0–80 % | 24 | @ 35 °C initial temperature, BoL |
| 0–100 % | 43 | @ 35 °C initial temperature, BoL, C/10 CV condition |
Guidelines for Custom Cell Blocks Up to R2024a
The Simscape Battery Pack Builder has some guidelines for effectively using custom cell blocks:
- The custom cell model cannot have a variable called
power_dissipated. - If thermal effects are required, the model must have at least one port or node of type: thermal domain.
- If a key cell model block variable needs to be visible in the Simulink canvas (e.g., using the Probe block), then this variable must be set public without any restrictions on the
ExternalAccess. Otherwise, the variable will only be visible in the simulation log for postprocessing.
Module to Pack Simulations
Following the same process as above, we can create Simulink models for the module block generated above and for larger battery blocks, such as a pack. Then we can couple these blocks to the same parallel assembly charging control block, which relies on the 2D cell-charging map. Table 6 contains a summary of these simulations. In general, fast-charge time increases by a small amount with the current module and pack designs due to increased temperature spreads and higher temperatures on some of the cells.
Conclusions
- Our investigation of battery fast-charge times using Simscape Battery and About:Energy blocks and parameters has demonstrated the importance of a methodical multiscale approach from individual cell modeling to pack simulations. We highlight the importance of integrating About:Energy TSPMe and electrical models with detailed pack models enabled by Simscape Battery to ensure accuracy and safety in battery management systems, augmenting ongoing advancements in the field of battery charging. The key uncertainties around these predicted fast-charge times are mainly due to model resolution (e.g., electrothermal discretization), modeling assumptions, and the accuracy of the electrochemical/ECM model used. In general, higher model discretization or resolution will yield more accurate results.
- As shown with the cell-to-pack workflow, battery fast-charge times are a function of a wide array of variables, and battery pack designs can have a substantial impact. Starting at the cell level, the fastest rate at which a battery cell can charge depends on lithium diffusion and transport processes happening at small scales. At the module and pack level, other variables become important, such as DC charger current limit, number of cells in parallel, battery pack nominal voltage (400-volt versus 800-volt), intracell and intercell temperature spreads, intracell and intercell SOC spreads, non-cell resistance, among others. As shown in this article, these variables, specifically temperature differences, can have an important effect in charging rates, so it is paramount that they are considered in battery virtual design and verification workflows.
The following diagram shows the predicted cell-to-pack battery fast-charge times for the 400-volt system studied in this article (Figure 13).
batteries = ["Cell","Parallel Assembly","Module", "Pack"]; batteries0To80ChargeTimes = [ChargeTime0To80 pSetChargeTime0To80 moduleChargeTime0To80 packChargeTime0To80]; batteries0To100ChargeTimes = [ChargeTime0To100 pSetChargeTime0To100 moduleChargeTime0To100 packChargeTime0To100]; figure("Color","w") subplot(1,2,1) bar(batteries,batteries0To80ChargeTimes) ylabel("0 to 80% SOC Charge Time (min)") grid on subplot(1,2,2) bar(batteries,batteries0To100ChargeTimes) ylabel("0 to 100% SOC Charge Time (min)") grid on
Published 2024