comm.CRCGenerator
Generate CRC code bits and append to input data
comm.CRCGenerator will be removed in a future release. Use crcGenerate
instead. (since R2024b) For information on updating your code, see Version History.
Description
The comm.CRCGenerator
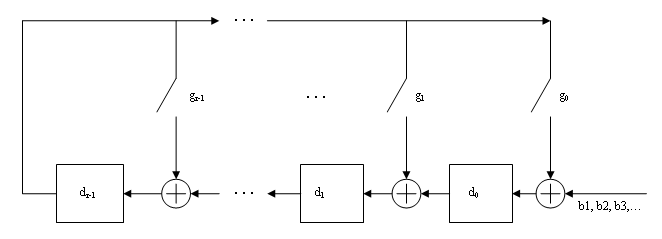
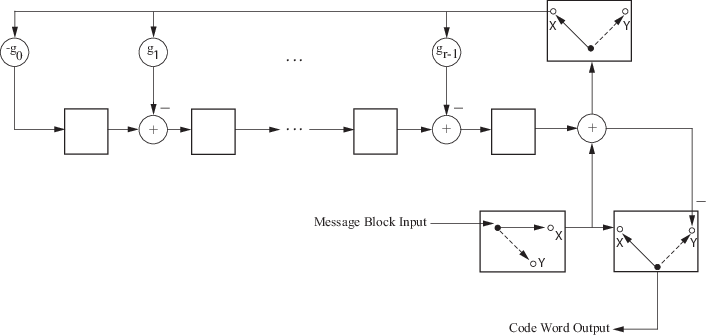
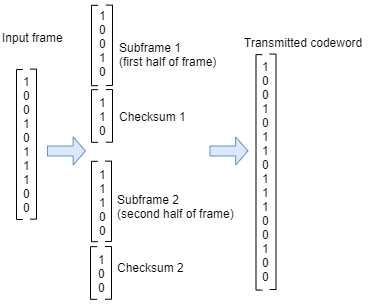
System object™ generates cyclic redundancy check (CRC) code bits for each input frame and
appends them to the frame. For more information, see CRC Generator Operation.
To generate CRC code bits for each input frame and append them to the frame:
Create the
comm.CRCGeneratorobject and set its properties.Call the object with arguments, as if it were a function.
To learn more about how System objects work, see What Are System Objects?
Creation
Syntax
Description
crcgenerator = comm.CRCGenerator
crcgenerator = comm.CRCGenerator(Name,Value)comm.CRCGenerator('Polynomial','z^16 + z^14 + z + 1') configures the
CRC generator System object to append CRC-16 cyclic redundancy check bits to the input frame. Enclose
each property name in quotes.
crcgenerator = comm.CRCGenerator(poly,Name,Value)Polynomial property
set to poly, and the other specified properties set to the specified
values.
Properties
Usage
Description
Input Arguments
Output Arguments
Object Functions
To use an object function, specify the
System object as the first input argument. For
example, to release system resources of a System object named obj, use
this syntax:
release(obj)
Examples
Algorithms
References
[1] Sklar, Bernard. Digital Communications: Fundamentals and Applications. Englewood Cliffs, N.J.: Prentice-Hall, 1988.
[2] Wicker, Stephen B. Error Control Systems for Digital Communication and Storage. Upper Saddle River, N.J.: Prentice Hall, 1995.