Models with Tunable Coefficients
Tunable Generalized LTI Models
Tunable Generalized LTI models represent systems having both fixed and tunable (or parametric) coefficients.
You can use tunable Generalized LTI models to:
Model a tunable (or parametric) component of a control system, such as a tunable low-pass filter.
Model a control system that contains both:
Fixed components, such as plant dynamics and sensor dynamics
Tunable components, such as filters and compensators
You can use tunable Generalized LTI models for parameter studies. For an example,
see Study Parameter Variation by Sampling Tunable Model. You can also
use tunable Generalized LTI models for tuning fixed control structures using tuning
commands such as systune or the Control System Tuner app. See
Multiloop, Multiobjective Tuning.
Modeling Tunable Components
Control System Toolbox™ includes tunable components with predefined structure called Control Design Blocks. You can use tunable Control Design Blocks to model any tunable component that fits one of the predefined structures.
To create tunable components with a specific custom structure that is not covered by the Control Design Blocks:
For examples of creating such custom tunable components, see:
Modeling Control Systems with Tunable Components
To construct a tunable Generalized LTI model representing a control system with both fixed and tunable components:
Model the nontunable components of your system using numeric LTI models.
Model each tunable component using Control Design Blocks or expressions involving such blocks. See Modeling Tunable Components.
Use model interconnection commands such as
series,parallelorconnect, or the arithmetic operators+,-,*,/,\, and^, to combine all the components of your system.
The resulting model is:
A
genssmodel, if none of the nontunable components is a frequency response data model (for example,frd)A
genfrdmodel, if the nontunable component is afrdmodel
For an example of constructing a genss model of a control
system with both fixed and tunable components, see Control System with Tunable Components.
Internal Structure of Generalized Models
A Generalized model separately stores the numeric and parametric portions of the model by structuring the model in Standard Form, as shown in the following illustration.
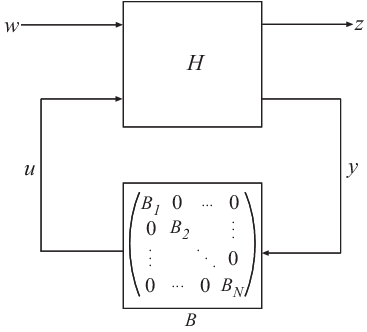
w and z represent the inputs and outputs of the Generalized model.
H represents all portions of the Generalized model that have fixed (non-parametric) coefficients. H is:
A state-space (
ss) model, forgenssmodelsA frequency response data (
frd) model, forgenfrdmodelsA matrix, for
genmatmodels
B represents the parametric components of the Generalized
model, which are the Control Design Blocks
B1, . . . , BN.
The Blocks property of the Generalized model stores a list of the
names of these blocks. If the Generalized model has blocks that occur multiple times
in
B1, . . . , BN,
these are only listed once in the Blocks property.
To access the internal representation of a Generalized model, including
H and B, use the getLFTModel command.
This Standard Form can represent any control structure. To understand why, consider the control structure as an aggregation of fixed-coefficient elements interacting with the parametric elements:
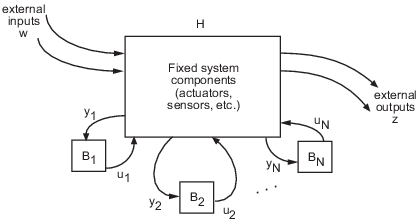
To rewrite this in Standard Form, define
and group the tunable control elements B1, . . . , BN into the block-diagonal configuration C. P includes all the fixed components of the control architecture—actuators, sensors, and other nontunable elements—and their interconnections.