fndir
Directional derivative of function
Syntax
df = fndir(f,y)
Description
df = fndir(f,y) is the ppform of the
directional derivative, of the function f in
f, in the direction of the (column-)vector y.
This means that df describes the function .
If y is a matrix, with n columns, and
f is d-valued, then the function in
df is prod(d)*n-valued. Its value at
x, reshaped to be of size [d,n], has in
its jth “column” the directional derivative of
f at x in the direction of the
jth column of y. If you prefer
df to reflect explicitly the actual size of
f, use instead
df = fnchg( fndir(f,y), 'dim',[fnbrk(f,'dim'),size(y,2)] );
Since fndir relies on the ppform of the function in
f, it does not work for rational functions nor for functions
in stform.
Examples
For example, if f describes an m-variate
d-vector-valued function and x is some
point in its domain, then, e.g., with this particular ppform f
that describes a scalar-valued bilinear polynomial,
f = ppmak({0:1,0:1},[1 0;0 1]); x = [0;0];
[d,m] = fnbrk(f,'dim','var');
jacobian = reshape(fnval(fndir(f,eye(m)),x),d,m)
is the Jacobian of that function at that point (which, for this particular scalar-valued function, is its gradient, and it is zero at the origin).
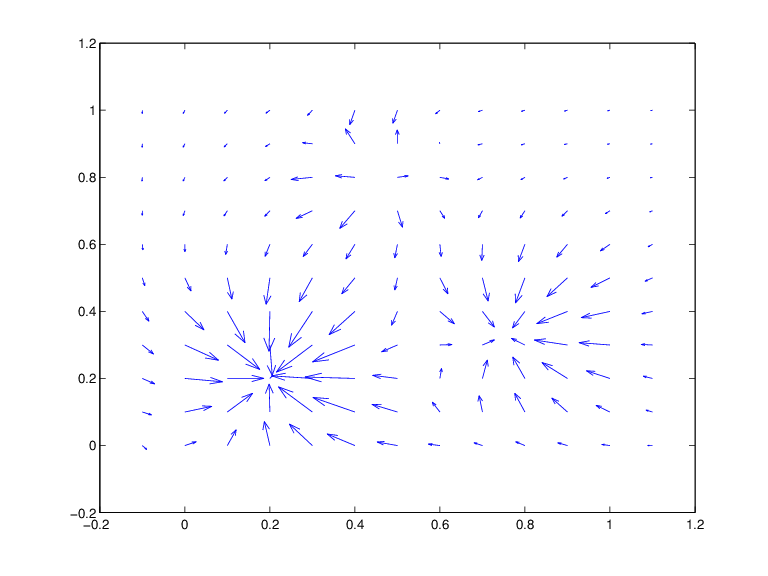
As a related example, the next statements plot the gradients of (a good approximation to) the Franke function at a regular mesh:
xx = linspace(-.1,1.1,13); yy = linspace(0,1,11);
[x,y] = ndgrid(xx,yy); z = franke(x,y);
pp2dir = fndir(csapi({xx,yy},z),eye(2));
grads = reshape(fnval(pp2dir,[x(:) y(:)].'),...
[2,length(xx),length(yy)]);
quiver(x,y,squeeze(grads(1,:,:)),squeeze(grads(2,:,:)))
Here is the resulting plot.
Algorithms
The function in f is converted to ppform, and the directional
derivative of its polynomial pieces is computed formally and in one vector
operation, and put together again to form the ppform of the directional derivative
of the function in f.